一些概念
- 排序算法的稳定性:经过排序后,能使关键字相同的元素保持原顺序中的相对位置不变。
插入排序
直接插入排序
口语描述:前面一段排序好的序列,后面一段乱序的序列,每次从乱序的第一个往前移,移到在顺序序列中比它小的元素之后。
Note:适用情况,元素数目少,或者元素的初始序列基本有序
准确描述:n个待排序的元素由一个有序表和一个无序表组成,开始时有序表中只包含一个元素。排序过程中,每次从无序表中抽出第一个元素,将其插入到有序表中的适当位置,使有序表的长度不断加长,完成排序过程。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#define MAXSIZE 20
typedef int Keytype; //定义关键字为整型
typedef struct{
KeyType key; //关键字项
InfoType otherinfo; //其他数据项
}RedType //记录类型
typedef struct{
RedType r[MAXSIZE+1]; //r[0]闲置或用作哨兵
int length; //顺序表长度
}SqList; //顺序表类型
void InsertSort(SqList &L){
for(int i=2;i<=L.length;++i){
//如果没有这个if条件会怎么样? 直接
if(L.r[i].key<=L.r[i-1].key){
L.r[0] = L.r[i]; L.r[i] = L.r[i-1];
for(j=i-2; L.r[0].key<L.r[j].key;j--)
L.r[j+1] = L.r[j];
L.r[j+1] = L.r[0];
}
}
}
折半插入排序
口语描述:在直接插入排序的基础上,寻找插入位置时使用二分查找,称为折半插入排序。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void InsertSort(SqList &L){
for(int i=2;i<=L.length;++i){
L.r[0] = L.r[i];
L.r[i] = L.r[i-1];
low = 1; high = i-1;
while(low<=high){
mid = (low + high) / 2;
if(L.r[mid].key<L.r[0].key)
low = mid + 1;
else
high = mid - 1;
}
for(int j=i-1; j>=high+1;--j){
L.r[j+1] = L.r[j];
}
L.r[high+1] = L.r[0];
}
}
三个需要注意的点:
1、退出条件是 low <= high 不是 low < high
2、mid的取值 在数很大的时候担心溢出应采用low+(high-low)/2这种写法
3、low与high的更新:应当是low = mid+1 high = mid-1 避免死循环
希尔排序
口语描述:选一个增量,相当于把一个序列分成了分成了增量个数个子序列,举个例子,比如132456,增量为2的话,就分成了,125, 346,然后再对子序列排序。当增量足够小时,再对全体元素进行一次插入排序。
Note:希尔排序是一种不稳定的排序算法
代码(以dlta[k]为增量的希尔排序):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
// 一趟希尔排序,和直接插入的排序就是每次往前走一个,变成了每次往前走dk个
// 最后元素后移的结束条件多了一个j>0,因为现在的L.r[0]仅起到暂存作用
// L.r[0]并不是此时并不是哨兵
void ShellInsert(SqList &L, int dk){
for(i=dk+1;i<=L.length;i+=dk){
if(L.r[i].key<L.r[i-dk].key){
L.r[0] = L.r[i];
for(j=i-dk;j>0&&L.r[0].key<L.r[j].key;j-=dk)
L.r[j+dk] = L.r[j];
L.r[j+dk] = L.r[0];
}
}
}
//总共进行t趟希尔排序,每次增量为dlta[]中的元素
//这里我觉得dlta[t-1]应该是等于1,因为最后要进行一次直接插入排序嘛
void ShellSort(SqList &L, int dlta[], int t){
for(k=0;k<t;k++){
ShellInsrt(L, dlta[k]);
}
}
王道代码(每次增量为dk/2):
1
2
3
4
5
6
7
8
9
10
11
12
13
void ShellInsert(SqList &L, int n){
for(int dk=n/2;dk>=1;dk=dk/2){
for(int i=dk+1;i<=L.length;i+=dk){
if(L.r[i].key<L.r[i-dk].key){
L.r[0] = L.r[i];
for(int j=i-dk;j>0&&L.r[j].key>L.r[0].key;j-=dk){
L.r[j+dk] = L.r[j];
}
L.r[j+dk] = L.r[0];
}
}
}
}
交换排序
冒泡排序
口语描述:相邻两个比较,若为逆序则交换。两趟for循环。第一趟用于改变第二趟比较的长短,注意,我总是分不清冒泡排序和选择排序。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void BubbleSort(SqList &L){
// 注意,这里的flag用的很灵性,如果比较一趟,发现序列有序
// 就不需要再进行比较了,这样省去了很多趟的比较
for(int i=1, change=True;i<=L.length&&change;++i){
change = False;
for(int j=1;j<=L.length-i+1;++j){
if(L.r[j].key>L.r[j+1].key){
L.r[0] = L.r[j];
L.r[j] = L.r[j+1];
L.r[j+1] =L.r[0];
chage = True;
}
}
}
}
快速排序
口语描述:
- 序列中取一个元素,以这个元素为基准,把序列分成两个子序列(一半比基准元素小,一半比基准元素大)
- 对两个子序列重复1
- 重复1,2,直到整个序列有序。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void QuickSort(SqList &L, int low, int high){
if(low < high){
int pivotpos = Partition(L, low, high);
QuickSort(L, low, pivotpos-1);
QuickSort(L, pivotpos+1, high);
}
}
int Partition(SqList &L, int low, int high){
L.r[0] = L.r[low];
while(low<high){
while(low<high&&L.r[high].key>=L.r[0].key) --high;
L.r[low] = L.r[high];
while(low<high&&L.r[low].key<=L.r[0].key) ++low;
L.r[high] = L.r[low];
}
L.r[low] = L.r[0];
return low;
}
选择排序
简单选择排序
口语描述:每次选一个最小的数和和前面的数交换。第i趟在n-i+1个记录中选取最小的记录作为有序序列中的第i个记录。
代码:
1
2
3
4
5
6
7
void SelectSort(SqList &L){
for(int i=1; i<L.length; ++i){
for(k=i+1,j=i;k<=L.length;k++)
if(L.r[k].key<L.r[j].key) j = k;
if(j!=i) swap(L.r[i],L.r[j]);
}
}
树形选择排序
口语描述:每一轮都将序列两两进行比较,小的进入下一轮,直到选出最小的
堆排序
口语描述: 堆的定义: 大顶堆: \(\begin{cases} K_i \geq K_{2i} \\ K_i \geq K_{2i+1} \end{cases}\)
小顶堆: \(\begin{cases} K_i \leq K_{2i} \\ K_i \leq K_{2i+1} \end{cases}\)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
void HeapSort(HeapType &H){
for(i=H.length/2;i>0;--i)
HeapAdjust(H, i, H.length);
for(i=H.length;i>1;--i){
swap(H.r[1],H.r[i]);
HeapAdjust(H, 1, i-1);
}
}
void HeapAdjust(HeapType &H, int s, int m){
rc = H.r[s];
//为什么是j<=m?
//j<m时,j没到叶子节点
//j=m时,j在叶子节点上,要看叶子节点和目标节点是否满足堆定义
for(j=2*s;j<=m;j*=2){
//为什么j<m?
//说明j还没到叶子节点
if(j<m&&H.r[j].key>H.r[j+1].key) ++j;
if(rc.key<H.r[j].key) break;
//s永远指向上一层的结点
//j永远指向下一层的兄弟节点中较小的那一个
//当j没到叶子节点时,且不满足堆定义
//将两个兄弟之间较小的直接覆盖掉s
H.r[s] = H.[j];
//更新指针s
s = j;
}
H.r[s] = rc;
}
归并排序
将n个无需序列看成n个由长度为1的有序子序列组成的序列,然后两两归并,得到n/2个长度为2或1的有序子序列,再两两归并,知道序列有序。
归并两个顺序表
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void SqList_Merge(SqList &LA, SqList &LB, SqList &LC){
int i=0, j=0, k = 0;
ElemType *pA = LA.r, *pB = LB.r, *pC;
LC.length = LA.length + LB.length;
pC = LC.r = (ElemType*)realloc(r, LC.length*sizeof(ElemType*));
while(pA<pA+LA.length&&pB<pB + LB.length){
if(*pA < *PB){
*pC++ = *pA++;
}
else{
*pC++ = *pB++;
}
}
while(pA<pA+LA.length) *pC++ = *pA++;
while(pB<pB+LB.length) *pC++ = *pB++;
}
归并两个单链表
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void LinkList_Merge(LinkList &LA, LinkList &LB){
LNode *pA = LA->next, *pB = LB->next;
LNode *pC = LA;
while(pA!=NULL&&pB!=NULL){
if(pA->Val < pB->Val){
pC->next = pA;
pA = pA->next;
}else{
pC->next = pB
pB = pB->next;
}
}
if(pA!=NULL) pC->next = PA;
if(pB!=NULL) pC->next = PB;
}
基数排序
以比较三位数为例 先比较个位,按顺序排列,再比较十位,按顺序排列,最后比较百位,按顺序排列。
| 时间复杂度 | 空间复杂度 | 稳定性 | 适用情况 | |
|---|---|---|---|---|
| 直接插入排序 | $O(n^2)$ | O(1) | 稳定 | n较小,初始序列基本有序 |
| 希尔排序 | $O(n^{1.3})$ | O(1) | 不稳定 | |
| 冒泡排序 | $O(n^{2})$ | O(1) | 稳定 | n较小,初始序列基本有序 |
| 快速排序 | $O(n\log_2{n})$ | $O(\log_2{n})$ | 不稳定 | 初始序列无序 |
| 简单选择排序 | $O(n^{2})$ | O(1) | 不稳定 | n较小 |
| 堆排序 | $O(n\log_2{n})$ | O(1) | 不稳定 | n较大,或只排前几位 |
| 2-路归并排序 | $O(n\log_2{n})$ | O(n) | 稳定 | n很大 |
| 链式基数排序 | $O(d(n+rd))$ | O(rd) | 稳定 | n大,关键字值小 |
Note:快速排序在最坏的情况下退化成冒泡排序,时间复杂度为$O(n^2)$, 快速排序每次递归都会返回一个中间值的位置,必须使用栈。所以空间复杂度就是栈用的空间。
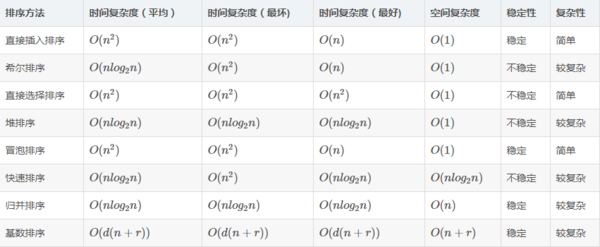
这个图有问题 希尔排序平均时间复杂度为$O(n^{1.3})$ 快速排序空间复杂度为$O(logn)$