生成模型与判别模型
判别模型
判别模型,像分类一样, 通过判别界限去区分样本。
从概率的角度分析就是获取样本x属于类别y的概率$P(y|x)$
生成模型
生成模型需要在整个条件内产生数据的分布,去拟合整个分布。
从概率的角度讲就是样本x在整个分布中的产生的概率,即联合概率密度P(xy)
GAN的实现过程
前向传播阶段
模型输入 以图片生成为例
对于生成器
模型的输入为噪声$z$(一般为高斯噪声)
对于判决器
模型的的输入为真实数据$(x, 1)$和经过生成器噪声$(G(z), 0)$
模型输出
对于生成器
模型的输出为$G(z)$,即$Image_{fake}$
对于判决器 模型的输出为一个0到1之间的数,表示输入图片为Real Image的概率
反向传播阶段
优化目标
\[\min_D \max_G V(D, G) = E_{x\thicksim P_{data}(x)}[log (D(x))] + E_{x\thicksim P_{z}(z)}[log (1 - D(G(z))]\]这个公式含义是, 先优化D, 再优化G, 拆解之后为如下两步
第一步:优化D
\[\max_D V(D, G) = E_{x\thicksim P_{data}(x)}[log (D(x))] + E_{z\thicksim P_{z}(z)}[log (1 - D(G(z))]\]对于真样本$x$, D的结果越大越好,因为真样本的预测结果越接近1越好。
对于假样本$G(z)$, D的结果越小越好,也就是$D(G(z))$越小越好,因为它的标签是0。
若第二项写为$E_{z\thicksim P_{z}(z)}[log (D(G(z))]$ 但是第一项越大,第二项越小,与我们将V(D, G)最大矛盾, 因此将第二项写为$E_{z\thicksim P_{z}(z)}[log (1 - D(G(z))]$, 这样就是越大越好
第二步:优化G
\[\min_G V(D, G) = E_{z\thicksim P_z{z}}[log (1 - D(G(z))]\]在优化G的时候,没有真样本什么事,所以把第一项直接去掉。
此时只有假样本, 但希望假样本的标签是1,所以是D(G(z))越大越好, 但是为了统一成$1 - D(G(z))$的形式, 那么只能最小化$1 - D(G(z))$, 本质上没有区别,只是为了形式上的统一。
这两个优化模型合并起来写,就是最开始的目标函数
判决器的损失函数
\[-((1-y)log(1-D(G(z))) + ylogD(x))\]这个就是逻辑回归里的交叉熵损失函数
当输入为real Image时,此时y=1, 仅需考虑第二项$logD(x)$。$D(x)$为判决器的输出,表示x为real数据的概率,我们的目的是让判决器的输出$D(x)$尽量靠近1。
对于判决器来说,用交叉熵损失函数计算loss,进行梯度反传,这里的梯度反传可以使用任意一种梯度修正的方法(f-divergence的结论)。
生成器的损失函数
\[(1-y)log(1-D(G(z)))\]当输入为fake Image时,y=0, 故损失函数即为$log(1-D(G(z)))$。
对于生成器来说,我们要做的是让$G(z)$产生的数据尽可能的和数据集中的数据一样,即所谓的同样的分布。那么我们要做的就是最小化生成模型的误差,即只将由$G(z)$产生的误差传给生成模型。
但是针对判别模型的预测结果,对梯度变化的方向进行改变。
当判决器认为输出为真实数据集的时候,梯度为正。
当判决器认为输出为假数据的时候,梯度为负。
最终的损失函数为 \((1-y)log(1-D(G(z)))(2* \overline D(G(z)) - 1)\)
其中$\overline D$表示判决器的预测类别,对概率进行取整,即0或1, 用于更改梯度方向, 阈值可以自己设置, 一般来说是0.5。
GANs相关理论
GANs本质上在做什么
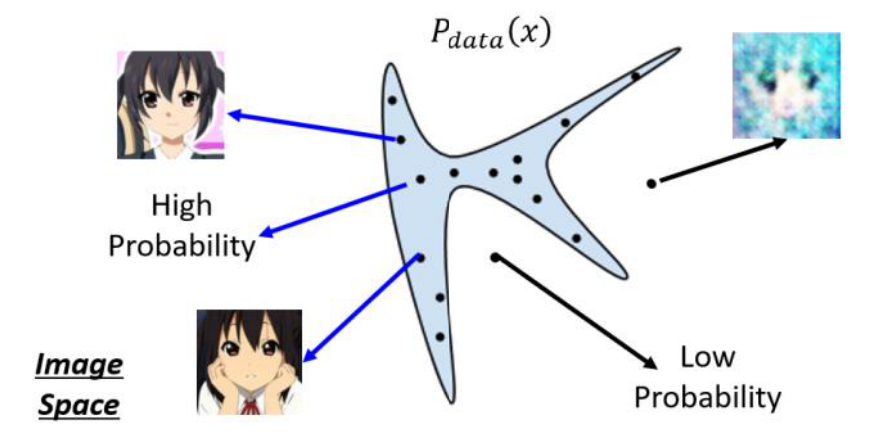
我们假设把每一个图片看作二维空间中的一个点, 并且现有图片会满足于某个数据分布, 我们记作$P_{data}(x)$。以人脸举例,在很大的一个图像分布空间中,实际上只有很小一部分的区域是人脸图像。如上图所示,只有在蓝色区域采样出的点才会看起来像人脸, 而在蓝色区域以外的区域采样出的点就不是人脸。 今天我们需要做的, 就是让机器去找到人脸的分布函数。具体来说,就是我们会有很多人脸图片数据,我们观测这些数据的分布,大致能猜测到\哪些区域出现人脸图片数据的概率比较高, 但是如果让我们找出一个具体的定义式, 去给明这些人脸图片数据的分布规律,我们是没有办法做到的。但是如今,我们有了机器学习,希望机器能够学习到这样一个分布规律,并能够给出一个极致贴合的表达式。 在 GANs 出现之前,人们采用的方法是Maximum Likelihood Estimation, 也就是极大似然估计。
Maximum Likelihood Estimation: \(L = \prod_{i=1}^{m}P_G(x^i; \theta)\)
找出一个最佳的参数组$\theta^{*}$,使得生成器的结果最接近P_{data}(x)。
证明: maximizing the likelihood 问题 等价于 求 minimize KL Divergence(KL Divergence 是一个衡量两个分布之间的差异的计算式)问题
比较复杂,现在能够理解,却无法自己推导,等有这个时间,有这个能力再更。
公式推导
信息量、熵、交叉熵、KL散度、JS散度
信息量
事件发生的概率为p(x), 它的信息量就是:
\[log \frac{1}{p(x)} = -log (p(x))\]熵
信息量的期望就是熵
\[H(x) = - \sum_{i=1}^{n}p(x_i)log(p(x_i))\]KL散度(相对熵)
事件A发生的概率为p(x), 事件B发生的概率为q(x), 那么事件A和B的KL散度为
\[D_{KL}(p(x) \| q(x)) = \sum_{i=1}^{n}p(x)log \frac{p(x)}{q(x)}\]想法:为什么KL散度能够衡量两个分布之间广义上的距离?
KL散度在信息论中有自己明确的物理意义,它是用来度量使用基于Q分布的编码来编码来自P分布的样本平均所需的额外的Bit个数。而其在机器学习领域的物理意义则是用来度量两个函数的相似程度或者相近程度。


交叉熵
KL散度可做如下推导:
\[D_{KL}(p(x) \| q(x)) = \sum_{i=1}^{n}p(x)log \frac{p(x)}{q(x)} \\ = \sum_{i=1}^{n}p(x)logp(x) - \sum_{i=1}^{n}p(x)logq(x) \\ = -H(x) + [- \sum_{i=1}^{n}p(x)logq(x)]\]后面那部分即为交叉熵:
\[H(p, q) = -\sum_{i=1}^{n}p(x_i)log(q(x_i))\]JS散度
KL散度不对称,即:
\[D_{KL}(p(x) \| q(x)) \neq D_{KL}(q(x) \| p(x))\]JS散度解决了这个问题, JS散度是对称的,其值在0到1之间:
\[JS(p(x)||q(x)) = \frac{1}{2}D_{KL}(p(x) \| \frac{p(x) + q(x)}{2}) + \frac{1}{2}D_{KL}(q(x) \| \frac{p(x) + q(x)}{2})\]Generative Adversrial Network
前向传播
训练Discriminator:
输入: x和G(z)
其中G(z)是Generator生成的图像
输出: Real or Fake
训练Generator
输入:z
其中z服从于标准正态分布
输出:G(z), G(z)为Generator生成的图像
反向传播
Discriminator的优化目标
\[\max_D V(D, G) = E_{x \thicksim P_{data}(x)}[log(D(x))] + E_{z \thicksim P_z(z)}[log (1- D(G(z)))]\]这个公式的意思就是,我们想让D尽可能的大, 这个过程不会优化G,将G(z)整个看成一个输入x。
在实现时,两项都是求了交叉熵,Discriminator的输出都在0到1之间,那么log之后的值域为负无穷到0之间, 再取负号,值域就在正无穷到0之间,我们想要D(x)趋向1, D(G(z))趋向0, 那么交叉熵就是趋向0。
式中是最大化,实现最小化。
Generator的优化目标
\[\min_G V(D, G) = E_{z \thicksim P_z(z)}[log (1 - D(G(z)))]\]此时训练生成器,与真样本无关,可以将第一项去掉,自变量为z, 我们希望当输入噪声z, Generator生成的图像G(z)能够骗过Discriminator, 也就是D(G(z))越大越好, 为了统一成$log (1 - D(G(z)))$的形式, 所以让$1-D(G(z))$越小越好。
问题: 既然G(z)送入Discriminator得到输出后,label为1, 计算交叉熵应该是$-log(D(G(z)))$, 怎么会是$log(1-D(G(z)))$呢?
解释:用交叉熵得到的是$-log (D(G(z)))$, 我们想要D(G(z))越大越好, D(G(z))的值域在0到1之间,那么取log值域就在负无穷到0之间,取负号值域就在正无穷到0之间,生成器训练的越好,loss越小。
上面也说了,是为了统一,所以代码用交叉熵应该也可以?
最终的优化目标:
\[\min_G \max_D V(D, G) = E_{x \thicksim P_{data}(x)}[log(D(x))] + E_{z \thicksim P_z(z)}[log (1- D(G(z)))]\]仔细观察发现,其实第一项就是输入x,label为1, Discriminator的输出的交叉熵的负数。
第二项是输入为G(z), label为0,Discriminator的输出的交叉熵的负数。
Wasserstein GAN
KL散度和JS散度的问题
\[D_{KL}(p(x) \| q(x)) = \sum_{i=1}^{n} p(x)log \frac{p(x)}{q(x)} \\ = \sum_{i=1}^{n}p(x)log p(x) - \sum_{i=1}^{n}p(x)log q(x) \\ = -H(x) + [- \sum_{i=1}^{n}p(x)log q(x)]\]前半部分是分布p的熵的负数, 后半部分是交叉熵。
KL散度衡量两个分布之间广义上的距离, 经过推导可以表现为交叉熵。
当两个分布之间完全没有重合时, KL散度是没有意义的。
思考:为什么? 解释:$\sum p(x)log p(x)$固定不动且有限, 所以重点是$-\sum p(x)log q(x)$, 当二者没有重合的时候,在$p(x) \neq 0$的时候, $q(x) = 0$, 这个时候D为无穷大。
当两个分布之间完全没有重合时, JS散度为常数。
\[JS(p(x) \| q(x)) = D_{KL}(p(x) \| \frac{p(x) + q(x)}{2}) + D_{KL}(q(x) \| \frac{p(x) + q(x)}{2})\]思考:为什么? 解释:当$p(x) \neq 0$, $q(x) = 0$时:
\[JS(p(x) \| q(x)) = D_{KL}(p(x) \| \frac{p(x))}{2}) + D_{KL}(q(x) \| \frac{p(x) }{2}) \\ = -\sum p(x)log \frac{p(x)}{\frac{p(x)}{2}} + -\sum q(x)log \frac{q(x)}{\frac{p(x)}{2}} \\ = -log2 \sum p(x)\]同理可得, 当$q(x) \neq 0$, $p(x) = 0$时:
\[JS(p(x) \| q(x)) == -log2 \sum q(x)\]当$q(x) = 0$, $p(x) = 0$时, JS散度为0.
Wasserstein距离
Discriminator的目标函数:
\[V(D, G) = \max_{D \in 1-Lipschitz} E_{x \thicksim P_{data}}[D(x)] - E_{x \thicksim P_G}[D(x)]\]其中$x \thicksim P_G$就是$x = G(z)$
Lipschitz约束, 利普希茨连续。满足如下性质的任意连续函数f称为 K-Lipschitz:
\[\mid f(x_1) - f(x_2) \mid \leq K \mid x_1 - x_2\mid\]直观上看,Lipschitz 条件限制了函数变化的剧烈程度。
Generator的目标函数:
\[V(D, G) = \max E_{z \thicksim p_g}(D(G(z)))\]WGAN
WGAN相较于DCGAN作了如下改动:
- Discriminator最后不做sigmoid
- 损失函数不使用log_loss
- 不使用基于动量的优化器
- 更新判决器,将判决器的参数值限定在一定范围c