熵
事件发生的概率为$p(x)$, 那么它的信息量是:
\[log~\frac{1}{p(x)} = -log~p(x)\]信息量的期望就是熵:
\[H(x) = -\sum_{i=1}^{n}p(x_i)log(p(x_i))\]0-1分布()的熵计算方法:
\[H(x) = -\sum_{i=1}^{n}p(x_i)log(p(x_i)) = -p(x)log(p(x)) - (1-p(x))log(1-p(x))\]“二项分布就是重复n次独立的伯努利试验。在每次试验中只有两种可能的结果,而且两种结果发生与否互相对立,并且相互独立,与其它各次试验结果无关,事件发生与否的概率在每一次独立试验中都保持不变,则这一系列试验总称为n重伯努利实验,当试验次数为1时,二项分布服从0-1分布。”
相对熵(KL散度)
什么是KL散度
当为离散的随机变量时:
\[D_{KL}(p|q) = \sum_{i=1}^{n}p(x_i)log(\frac{p(x_i)}{q(x_i)})\]当为连续的随机变量时:
\[D_{KL}(P_r||P_g) = \int P_r(x) log(\frac{P_r(x)}{P_g(x)})d\mu(x)\]在机器学习中, P往往用来表示样本的真实分布, Q用来表示模型所预测的分布,那么KL散度可以计算计算两个分布的差异, 也就是Loss损失值。
如果$q(x_i)$大于$p(x_i)$, 那么$log(\frac{p(x_i)}{q(x_i)})$为负
如果$q(x_i)$小于$p(x_i)$, 那么$log(\frac{p(x_i)}{q(x_i)})$为正
如果$q(x_i)$等于$p(x_i)$, 那么$log(\frac{p(x_i)}{q(x_i)})$为0
然后用$p(x_i)$给$log(\frac{p(x_i)}{q(x_i)})$加权,求出$log(\frac{p(x_i)}{q(x_i)})$的期望
也就是说高概率的$p(x_i)$匹配区域比低概率的$p(x_i)$匹配区域更加重要。
因此$D_{KL}$的取值范围为0到inf。
有时会将KL散度称为KL距离,但它并不满足距离的性质:
- KL 散度是非对称,即$D(p|q)$ 不一定等于 $D(q|p)$
- KL散度不满足三角不等式
KL散度的实战—1维高斯分布
假设有两个随机变量$x_1, x_2$, 各自服从一个高斯分布$N_1(\mu, \sigma^2), N_2(0, 1)$。
我们知道
\[N(\mu, \sigma) = \frac{1}{\sqrt{2\pi\sigma^2}}e^{\frac{(x-\mu)^2}{2\sigma^2}}\]那么
\[KL(N(\mu, \sigma^2)||N(0, 1)) \\ = \int \frac{1}{\sqrt{2\pi\sigma^2}}e^{\frac{-(x - \mu)^2}{2\sigma^2}}(log(\frac{\frac{e^{\frac{-(x - \mu)^2}{2\sigma^2}}}{\sqrt{2\pi\sigma^2}}}{\frac{e^{\frac{-x^2}{2}}}{\sqrt{2\pi}}}))dx \\ = \int \frac{1}{\sqrt{2\pi\sigma^2}}e^{\frac{-(x - \mu)^2}{2\sigma^2}}log\{\frac{1}{\sqrt{\sigma^2}}e^{\frac{1}{2}[x^2-\frac{(x-\mu)^2}{\sigma^2}]}\}dx \\ = \frac{1}{2} \int \frac{1}{\sqrt{2\pi\sigma^2}}e^{\frac{-(x - \mu)^2}{2\sigma^2}}[-log\sigma^2 + x^2 - \frac{(x-\mu)^2}{\sigma^2}]dx\]整个积分结果分成三项
第一项就是$-log\sigma^2$乘以概率密度的积分(也就是1),所以结果是$-log\sigma^2$
第二项实际是正态分布的二阶矩$EX^2$,其值等于$\mu^2 + \sigma^2$
根据定义,第三项其实就是”-方差除以方差=-1”
所以结果就是:
\[KL(N(\mu, \sigma^2)||N(0, 1)) = \frac{1}{2}(-log\sigma^2 + \mu^2 + \sigma^2 - 1)\]请重视并熟悉这个证明及结论,这会在VAE中用到。
交叉熵
将KL散度公式进行变形:
\[D_{KL} = \sum_{i=1}^{n}p(x_i)log(\frac{p(x_i)}{p(x_i)}) = \sum_{i=1}^{n}p(x_i)log(q(x_i)) - \sum_{i=1}^{n}p(x_i)log(q(x_i)) = -H(p(x)) + [-\sum_{i=1}^{n}p(x_i)log(q(x_i))]\]等式前一部分是p的熵, 等式的后一部分, 就是交叉熵:
\[H(p, q) = -\sum_{i=1}^{n}p(x_i)log(q(x_i))\]对于分类任务,评估label和predicts之间的差距。 我们是已知label的分布的, p的熵是一个常数,所以在优化过程中只关注交叉熵就可以了。
JS散度
JS散度度量两个概率分布的相似度,基于KL散度的变体,解决了KL散度非对称的问题。
一般,JS散度是对称的, 其取值是0到1之间,定义如下:
\[JS(P_1||P_2) = \frac{1}{2}KL(P_1||\frac{P_1+P_2)}{2}) + \frac{1}{2}KL(P_2||\frac{P_1 + P_2}{2})\]Wasserstein距离
KL散度和JS散度存在的问题:
如果两个分布P、Q离得很远,完全没有重叠的时候,KL散度是没有意义的, 而JS散度值是一个常数。意味着这一点梯度为0, 梯度消失了。
Wasserstein距离
Wasserstein距离度量两个概率分布之间的距离, 定义如下:
\[W(P_1, P_2) = \inf_{\gamma \thicksim \Pi (P_1, P_2) }E_{(x, y)\thicksim \gamma}[|x - y|]\]$\Pi (P_1, P_2)$是$P_1$和$P_2$分布组合起来的所有可能的联合分布的集合。
对于每一个可能的联合分布$\gamma$, 可以从采样$(x, y)\thicksim \gamma$得到一个样本x和y, 并计算出这对样本的距离$\lVert x-y \Vert$, 所以可以计算该联合分布$\gamma$下,样本对距离的期望值$E(x, y) \thicksim \gamma[\Vert x - y \Vert$]即样本的均值等于分布的期望。
在所有的联合分布中能够对这个期望值取到的下界$infy \thicksim \Pi(P_1, P_2)E(x,y) \thicksim \gamma[\Vert x-y \Vert]$就是Wasserstein距离。
直观上可以把$E(x,y)∼γ[\Vert x−y \Vert]$理解为在$γ$这个路径规划下把土堆P1挪到土堆P2所需要的消耗。而Wasserstein距离就是在最优路径规划下的最小消耗。所以Wesserstein距离又叫Earth-Mover距离。
Wasserstein距离相比KL散度、JS散度的优越性在于,即便两个分布没有重叠,Wasserstein距离仍然能够反映它们的远近;而JS散度在此情况下是常量,KL散度可能无意义。WGAN本作通过简单的例子展示了这一点。考虑如下二维空间中的两个分布$P_1$和$P_2$,$P_1$在线段AB上均匀分布,$P_2$在线段CD上均匀分布,通过控制参数$\theta$可以控制着两个分布的距离远近。
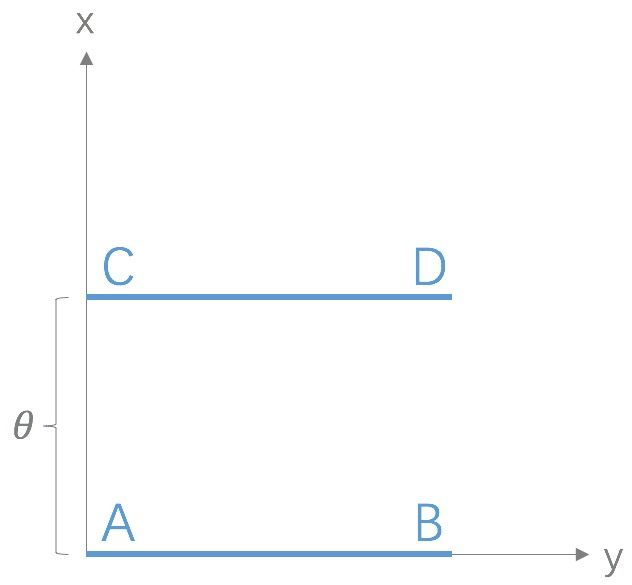
此时得到:
\[KL(P_1||P_2) = KL(P_1||P_2) = \begin{cases}+\infty & {if \theta \neq 0} \\ 0 & {if \theta = 0} \end{cases} (突变)\] \[JS(P_1||P_2) = \begin{cases}log2 & {if \theta \neq 0} \\ 0 & {if \theta = 0} \end{cases}(突变)\] \[W(P_0, P_1) = |\theta|(平滑)\]KL散度和JS散度是突变的,要么最大要么最小, Wasserstein距离却是平滑的,如果我们要用梯度下降法优化$\theta$这个参数,前两者根本提供不了梯度,Wasserstein距离却可以。类似地,在高维空间中如果两个分布不重叠或者重叠部分可忽略,则KL和JS既反映不了远近,也提供不了梯度,但是Wasserstein却可以提供有意义的梯度。
总结
损失函数的功能是通过样本来计算模型分布与目标分布间的差异, 在分布差异计算中,KL散度是最合适。
在实际中,某一事件的标签是已知不变的(例如我们设置猫的label为1,那么所有关于猫的样本都要标记为1),即目标分布的熵为常数。
KL散度 - 目标分布熵 = 交叉熵(这里的“-”表示裁剪)。所以我们不用计算KL散度,只需要计算交叉熵就可以得到模型分布与目标分布的损失值。
目标分布为常数为常数时, 模型分布与目标分布差异可用交叉熵代替KL散度。
如果目标分布是有变化的(如同为猫的样本,不同的样本,其值也会有差异),那么就不能使用交叉熵。