论文部分

两个场景

边际似然函数的积分$p_\theta(x) = \int p_\theta(z)p_\theta(x \arrowvert z)dz$难以计算（我们没办法估计边际似然分布，因为其中的后验分布$P_\theta(z \arrowvert x) = \frac{P_\theta(x \arrowvert z)P_\theta(z)}{P_\theta(x)}$难以计算，所以我们不能用EM算法）
一个大的数据集，批量优化成本太高。例如Monte Carlo EM算法，需要遍历所有数据进行采样，这样的代价过于高昂。

三个问题

参数$\theta$有效逼近ML(marginal likelihood)或者MAP(Maximum a posteriori estimation)估计。
对于参数$\theta$的选择给出观察值x的潜变量z的有效posterior inference，即$P_\theta(z \arrowvert x)$
有效逼近x的marginal inference

引入一个生成模型$q_\phi(z \arrowvert x)$逼近真正的后验分布$P_\theta(z \arrowvert x)$.

将$q_\phi(z \arrowvert x)$看作编码器(encoder)，编码器将产生一个高斯分布将z可能的值(x可能被生成的地方)，将$P_\theta(x \arrowvert z)$看作解码器(decoder)， z将产生一个关于分布x的值的可能性的分布。

Note:

In this case, we can let the variational approximate posterior be a multivariate Gaussian with a diagonal covariance structure:

\[logq_\phi(z\|x^{(i)}) = logN(z;\mu_{(i)}, \sigma^{2(i)}I)\]

在整个 VAE 模型中，我们并没有去使用 p(Z)（先验分布）是正态分布的假设，我们用的是假设 $p(Z \arrowvert X)$（后验分布）是正态分布。

\[p(Z) = \sum_X p(Z \arrowvert X)p(X) = \sum_X N(0 ,1)p(X) = N(0,1)\sum_X p(X) = N(0, 1)\]

这样我们就能达到我们的先验假设：p(Z) 是标准正态分布。

变分下限(The variational bound)

变分推断(variational inference)中常用的方法是求观察量x的似然函数：

\[log p_\theta(x^{(1)}, x^{(2)}, ..., x^{(N)}) = \sum_{i=1}^{N}logp_\theta (x^{(i)})\]

可以化成：

\[logp_\theta(x^{(1)}) = D_{KL}(q_\phi(z|x^{(i)})||p_\theta(z|x^{(i)})) +L(\theta, \phi; x^{(i)})\]

现在右边第一项为KL散度，可得：

\[logp_\theta(x^{(i)}) > L(\theta, \phi; x^{(i)}) = E_{q_{\phi}(z|x^{(i)})}[-logq_\phi(z|x) + logp_\theta(x, z)]\]

L函数也可以写成如下：

\[L(\theta, \phi; x^{(i)}) = -D_{KL}(q_\phi(z|x^{(i)})||p_\theta(z)) + E_{q_\phi(z|x^{(i)})}[logp_\theta(x^{(i)}|z)]\]

此时最大似然估计可以通过最大化L函数，但是其梯度计算难度较大。

证明： $L = log(p(x)) \\ = \sum_z q(z|x)log(p(x)) \\ = \sum_z q(z|x)log(\frac{p(z, x)}{p(z|x)}) \\ = \sum_z q(z|x)log(\frac{p(z, x)}{q(z|x)} \frac{q(z|x)}{p(z|x)}) \\ = \sum_z q(z|x)log(\frac{p(z, x)}{q(z|x)}) + \sum_z q(z|x)log(\frac{q(z|x)}{p(z|x)}) \\ = L^v + D_{KL}(q(z|x)\| p(z|x))$

因为KL散度大于0

所以$L \geq L^v$, $L^v$被称为L的变分下界

又因为$p(x)$是固定的， L是一个定值，我们如果想要最小化p和q之间的散度，就应该使$L^v$最大化。

\[L^v = \sum_z q(z|x)log(\frac{p(z, x)}{q(z|x)}) \\ = \sum_z q(z|x)log(\frac{p(x|z)p(z)}{q(z|x)}) \\ = \sum_z q(z|x)log(\frac{p(z)}{q(z|x)}) + \sum_z q(z|x)log(p(x|z))\] \[L^v = -D_{KL}(q(z|x)\|p(z)) + E_{q(z|x)}(log(p(x|z)))\]

如果使用蒙特卡洛梯度估计，梯度估计存在很高的方差:

\[E_{q_\phi(z|x^{(i)})}[f(z)] = E_{p(\epsilon)}[f(g_\phi(\epsilon, x^{(i)}))] \simeq \frac{1}{L}\sum_{l=1}^{L}f(g_\phi(\epsilon^{(l)}, x^{(i)})) \text {, where $\epsilon^{(l)} \thicksim p(\epsilon)$}\]

SGVB估计和AEVB算法

引入噪声变量(一般符合高斯分布)$\epsilon$和分布转换函数$g_\phi(\epsilon, x)$重写z这个潜变量$\tilde z \thicksim q_\phi(z \arrowvert x)$

\[\tilde z = g_\phi(\epsilon, x) \text {， with $\epsilon$ $\thicksim$ p($\epsilon$)}\]

使用蒙特卡洛估计函数（其中$f(x)$代指一些特殊的函数，例如$q_\phi(z \arrowvert x)$，等式最右边可以理解为L等分然后采样）：

利用Stochastic Gradient Vartiational Bayes(SGVB)给出L函数的估计

\[\tilde L^A(\theta, \phi; x^{(i)}) = \frac{1}{L} \sum_{i=1}^{L}log(p_\theta(x^{(i)}, z^{(i, l)}) - log(q_\phi(z^{(i, l)}|x^{(i)}))) \text {, where $z^{(i, l)} = g_\phi(\epsilon^{(i, l)}, x^{(i)})$ and $\epsilon^{(l)} \thicksim p(\epsilon)$}\]

该估计能够近似我们要求解的L函数

\[\tilde L^A(\theta, \phi; x^{(i)}) \simeq L(\theta, \phi;x^{(i)})\]

Auto Encoder Variational Bayes(AEVB)算法:

最大化L函数，求关于参数的梯度并且更新参数。回忆一下：

\[L(\theta, \phi; x^{(i)}) = -D_{KL}(q_\phi(z|x^{(i)})||P_\theta(z)) + E_{q_\phi(z|x^{(i)})}[log(q_\theta(x^{(i)}|z))]\]

其中

\[D_{KL}(q_\phi(z|x^{(i)})||P_\theta(z))\]

可以分解求出

证明：

假设有两个随机变量$x_1, x_2$, 各自服从一个高斯分布$N_1(\mu, \sigma^2)， N_2(0, 1)$。

我们知道

\[N(\mu, \sigma) = \frac{1}{\sqrt{2\pi\sigma^2}}e^{\frac{(x-\mu)^2}{2\sigma^2}}\]

那么

\[KL(N(\mu, \sigma^2)||N(0, 1)) \\ = \int \frac{1}{\sqrt{2\pi\sigma^2}}e^{\frac{-(x - \mu)^2}{2\sigma^2}}(log(\frac{\frac{e^{\frac{-(x - \mu)^2}{2\sigma^2}}}{\sqrt{2\pi\sigma^2}}}{\frac{e^{\frac{-x^2}{2}}}{\sqrt{2\pi}}}))dx \\ = \int \frac{1}{\sqrt{2\pi\sigma^2}}e^{\frac{-(x - \mu)^2}{2\sigma^2}}log\{\frac{1}{\sqrt{\sigma^2}}e^{\frac{1}{2}[x^2-\frac{(x-\mu)^2}{\sigma^2}]}\}dx \\ = \frac{1}{2} \int \frac{1}{\sqrt{2\pi\sigma^2}}e^{\frac{-(x - \mu)^2}{2\sigma^2}}[-log\sigma^2 + x^2 - \frac{(x-\mu)^2}{\sigma^2}]dx\]

整个积分结果分成三项

第一项就是$-log\sigma^2$乘以概率密度的积分（也就是1），所以结果是$-log\sigma^2$

第二项实际是正态分布的二阶矩$EX^2$，其值等于$\mu^2 + \sigma^2$

根据定义，第三项其实就是”-方差除以方差=-1”

所以结果就是：

\[KL(N(\mu, \sigma^2)||N(0, 1)) = \frac{1}{2}(-log\sigma^2 + \mu^2 + \sigma^2 - 1)\]

只有

\[E_{q_\phi(z|x^{(i)})}[log(p_\theta(x^{(i)})|z)]\]

是需要采样估计的。

这个是似然函数中L项的第一种写法

引入噪声变量化简式子，对上式化简得：

\[\tilde L^B(\theta, \phi; x^{(i)}) = -D_{KL}(q_\phi(z|x^{(i)})\|p_\theta(z)) + \frac{1}{L} \sum_{l=1}^{L}()log(p_\theta(x^{(1)}|z^{(i, l)}))\]

这是似然函数中L项的第二种写法

这里证明和上面是一样的，之所以写两遍，因为上下思路是连贯的，方便回顾。

因为KL散度大于0

所以$L \geq L^v$, $L^v$被称为L的变分下界

又因为$p(x)$是固定的， L是一个定值，我们如果想要最小化p和q之间的散度，就应该使$L^v$最大化。

然后给定数据集X(一共N个)，如果采用minibatch（一个batchM个数据），可以通过下面方式进行估计。实验证明，如果minibatch足够大（例如M=100），那么L函数的第二项L可以取1。

\[L(\theta, \phi; X) \simeq \tilde L^M(\theta, \phi; X^M) = \frac{N}{M}\sum_{i=1}^M \tilde L(\theta, \phi; x^{(i)})\]

第一项（z先验分布和给定x的z的后验分布的KL散度）充当正则项

第二项是自动编码的期望重构误差的负数。

函数$g_\phi()$是事先选择使得它能够映射数据集$x^{(i)}$和随机噪声$\epsilon$到$z$的后验分布（也就是$z^{(i, l)} \thicksim q_\phi(z \arrowvert x^{(i)})$）的一次采样，即$z^{(i, l)} = g_\phi(\epsilon^{(l)}, x^{(i)})$。

然后，将$z^{(i, l)}$代入$logp_\theta(x^{(i)} \arrowvert z^{(i, l)})$，也就是该生成模型的$x^{(i)}$的似然函数，这一项也是自动编码的重构误差的负数。

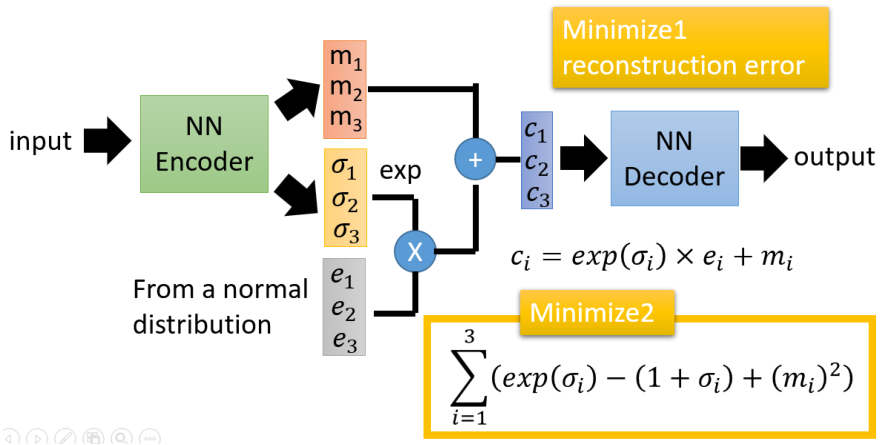
为什么minimize的对数变成了指数？

重参数技巧(Reparameterization Trick)

从一个分布中采样的时候因为采样这个动作是离散的，那么计算图就不能传递梯度，因此参数无法进行更新。

我们可以先假设概率分布服从一个高斯分布（或者多项式分布）那么这个概率分布可以表示成两个确定的参数，x和ϕ分别表示均值和标准差，因此输出的动作可以表示为z=x+ϵ⋅ϕ,ϵ是真正表示随机的变量，比如说是从标准正太分布中采样出来的一个值，这样，ϵ的值就在计算图之外，我们也不用更新，因此解决了采样导致梯度不可传递的问题，但是有一个限制条件就是我们必须制定，原来的概率分布是我们所规定的一个分布，比如说说正态分布或者是多项式分布。

实现部分

线性层

引入相关包

from __future__ import print_function
import argparse
import torch
import torch.utils.data
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torch.autograd import Variable
from torchvision import datasets, transforms
from torchvision.utils import save_image

参数初始化

parser = argparse.ArgumentParser(description='PyTorch MNIST Example')
parser.add_argument('--batch-size', type=int, default=64, metavar='N',
                    help='input batch size for training (default: 128)')
parser.add_argument('--epochs', type=int, default=10, metavar='N',
                    help='number of epochs to train (default: 10)')
parser.add_argument("--n_cpu", type=int, default=8, help="number of cpu threads to use during batch generation")
parser.add_argument("--n_gpu", type=int, default=1, help="number of gpu")
parser.add_argument("--latent_dim", type=int, default=32, help="dimensionality of the latent space")
parser.add_argument("--ngf", type=int, default=64, help="numbers of generator's features")
parser.add_argument("--ndf", type=int, default=64, help="numbers of discriminator's features")
parser.add_argument("--img_size", type=int, default=28, help="size of each image dimension")
parser.add_argument("--channels", type=int, default=1, help="number of image channels")
parser.add_argument('--seed', type=int, default=1, metavar='S',
                    help='random seed (default: 1)')
parser.add_argument('--log-interval', type=int, default=10, metavar='N',
                    help='how many batches to wait before logging training status')
args = parser.parse_known_args()[0]
args.cuda = True if torch.cuda.is_available() else False
print(args)

#Sets the seed for generating random numbers. And returns a torch._C.Generator object.
#torch.manual_seed(args.seed)
if args.cuda:
    torch.cuda.manual_seed(args.seed)   

加载数据集

kwargs = {'num_workers': 1, 'pin_memory': True} if args.cuda else {}
trainset = datasets.MNIST('../data', train=True, download=True,transform=transforms.ToTensor())
train_loader = torch.utils.data.DataLoader(
    trainset,
    batch_size=args.batch_size, shuffle=True, **kwargs)
image, label = trainset[0]  
print(len(trainset))
print(image.size())

构造VAE模型

class VAE(nn.Module):
    def __init__(self):
        super(VAE, self).__init__()

        self.fc1 = nn.Linear(784, 400)
        self.fc21 = nn.Linear(400, args.latent_dim)
        self.fc22 = nn.Linear(400, args.latent_dim)
        
        self.fc3 = nn.Linear(args.latent_dim, 400)
        self.fc4 = nn.Linear(400, 784)

        self.relu = nn.ReLU()
        self.sigmoid = nn.Sigmoid()

    def encode(self, x):
        h1 = self.relu(self.fc1(x))
        return self.fc21(h1), self.fc22(h1)

    def reparametrize(self, mu, logvar):
        std = logvar.mul(0.5).exp_()
        eps = Variable(std.data.new(std.size()).normal_())
        return eps.mul(std).add_(mu)

    def decoder(self, z):
        h3 = self.relu(self.fc3(z))
        return self.sigmoid(self.fc4(h3))

    def forward(self, x):
        mu, logvar = self.encode(x.view(-1, 784))
        z = self.reparametrize(mu, logvar)
        return self.decoder(z), mu, logvar

vae = VAE()
if args.cuda:
    vae.cuda()

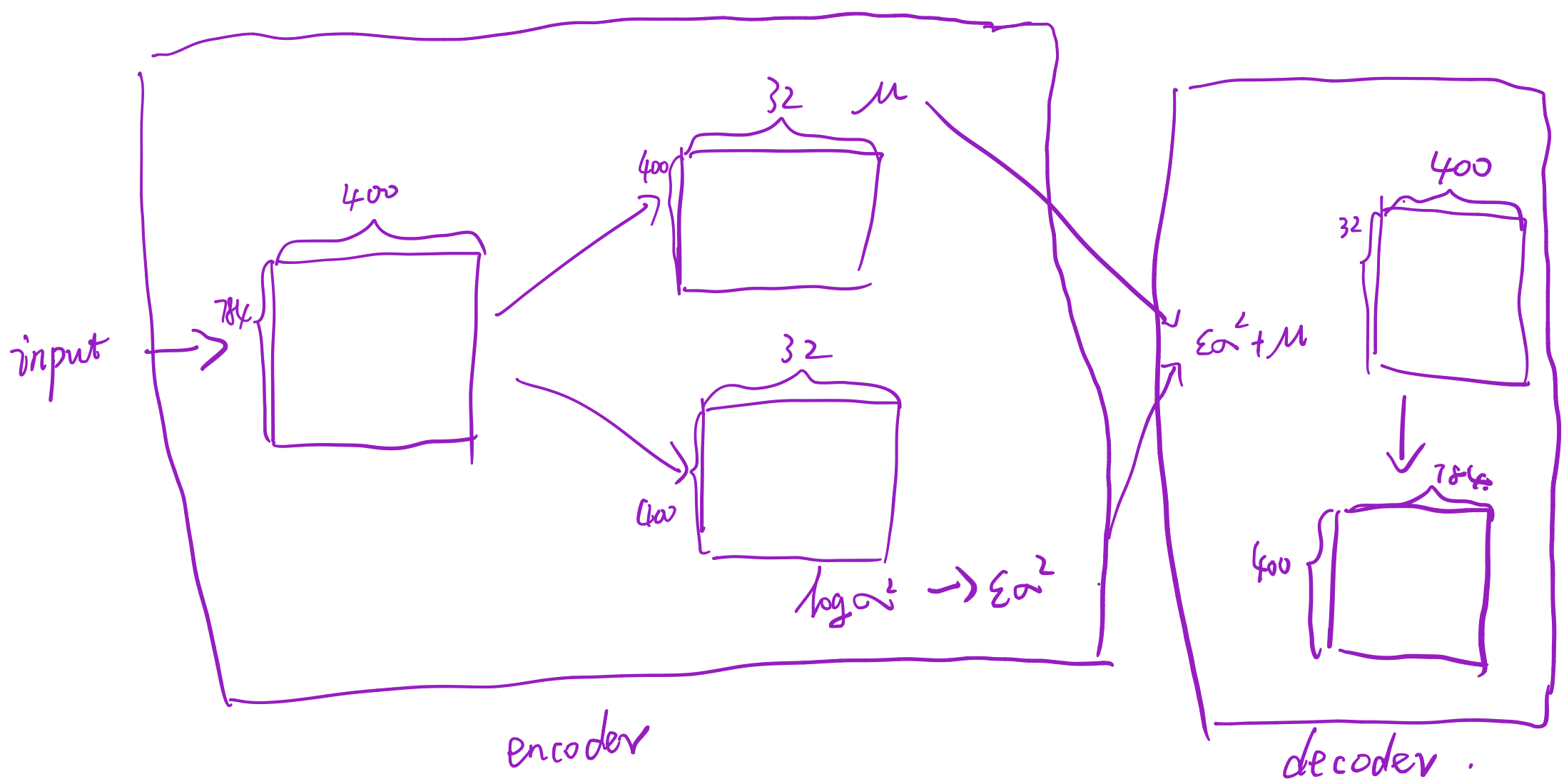
思考：这里的eps是个Variable，那么就应该会对它求导，那上文讲这个变量时随机抽样产生的，应该是不可导的矛盾。

损失函数及优化器

reconstruction_function = nn.BCELoss()
reconstruction_function.size_average = False

def loss_function(recon_x, x, mu, logvar):
    #BCE = reconstruction_function(recon_x, x.view(-1, 784))
    BCE = F.binary_cross_entropy(recon_x, x,  size_average=False)

    # see Appendix B from VAE paper:
    # Kingma and Welling. Auto-Encoding Variational Bayes. ICLR, 2014
    # https://arxiv.org/abs/1312.6114
    # 0.5 * sum(1 + log(sigma^2) - mu^2 - sigma^2)
    KLD_element = mu.pow(2).add_(logvar.exp()).mul_(-1).add_(1).add_(logvar)
    KLD = torch.sum(KLD_element).mul_(-0.5)

    return BCE + KLD


#optimizer = optim.Adam(model.parameters(), lr=0.1)
optimizer =  optim.Adam(vae.parameters(), lr=0.001, betas=(0.9, 0.999), eps=1e-08, weight_decay=0)

遇到的问题：nn.BCELoss()和F.binary_cross_entropy本应该是一样的，但是结果却不一样。

训练

def train():
    vae.train()
    total_loss = 0
    for i, (data, _) in enumerate(train_loader, 0):
        data = Variable(data).cuda(0)
        optimizer.zero_grad()
        recon_x, mu, logvar = vae.forward(data)
        loss = loss_function(recon_x, data, mu, logvar)
        loss.backward()
        total_loss += loss.item()
        optimizer.step()
        
        if i % args.log_interval == 0:
            sample = Variable(torch.randn(64, args.latent_dim)).cuda()
            #print(sample)
            sample = vae.decoder(sample).cpu()
            save_image(sample.data.view(64, 1, 28, 28),
                       'result_Linear/' + str(epoch) + '.png')
            print('Train Epoch:{} -- [{}/{} ({:.0f}%)] -- Loss:{:.6f}'.format(
                epoch, i*len(data), len(train_loader.dataset), 
                100.*i/len(train_loader), loss.item()/len(data)))

for epoch in range(1, args.epochs + 1):
    train()

实验结果

卷积层

除了VAE模型，其他地方都与线性层是一样的

VAE模型

class VAE(nn.Module):
    def __init__(self):
        super(VAE, self).__init__()
        
        self.encoder = nn.Sequential(
                nn.Conv2d(1, 64, kernel_size=4, stride=2, padding=1),
                nn.BatchNorm2d(64),
                nn.LeakyReLU(0.2, inplace=True),
            
                nn.Conv2d(64, 128, kernel_size=4, stride=2, padding=1),
                nn.BatchNorm2d(128),
                nn.LeakyReLU(0.2, inplace=True),
            
                nn.Conv2d(128, 128, kernel_size=3, stride=1, padding=1),
                nn.BatchNorm2d(128),
                nn.LeakyReLU(0.2, inplace=True),
                )
        
        self.fc11 = nn.Linear(128 * 7 * 7, args.latent_dim)
        self.fc12 = nn.Linear(128 * 7 * 7, args.latent_dim)
        self.fc2 = nn.Linear(args.latent_dim, 128 * 7 * 7)
        
        self.decoder = nn.Sequential(
                nn.ConvTranspose2d(128, 64, kernel_size=4, stride=2, padding=1),
                nn.ReLU(inplace=True),
            
                nn.ConvTranspose2d(64, 1, kernel_size=4, stride=2, padding=1),
                nn.Sigmoid()
                )
        
    def reparameterize(self, mu, logvar):
        eps = Variable(torch.randn(mu.size(0), mu.size(1))).cuda()
        z = mu + eps * torch.exp(logvar/2)
        
        return z
    
    def forward(self, x):
        out1, out2 = self.encoder(x), self.encoder(x)
        mu = self.fc11(out1.view(out1.size(0), -1))
        logvar = self.fc12(out2.view(out2.size(0), -1))
        z = self.reparameterize(mu, logvar)
        out3 = self.fc2(z).view(z.size(0), 128, 7, 7)
        
        return self.decoder(out3), mu, logvar

【深度学习笔录】VAE论文阅读及其实现