VAE 深度学习

【深度学习笔录】CVAE论文阅读及其实现

Posted by ShawnD on January 19, 2020

论文部分

VAE相关内容回顾

变分下限(variational lower bound)：

\[logp_\theta(x) = KL(q_\phi(z \arrowvert x)\| p_\theta(z \arrowvert x)) + E_{q_\phi(z \arrowvert x)}[-logq_\phi(z \arrowvert x) + logp_\theta(x, z)]\]

第二项可以写为L函数：

\[L = E_{q_\phi(z \arrowvert x^{(i)})}[-logq_\phi(z \arrowvert x) + logp_\theta(x, z)]\]

也可以写成：

\[L = -D_{KL}(q_\phi(z \arrowvert x^{(i)})\|p_\theta(z)) + E_{q_\phi(z \arrowvert x^{(i)})}[logq_\theta(x^{(i)} \arrowvert z)]\]

证明：

\[L = E_{q_\phi(z \mid x^{(i)})}[-logq_\phi(z \mid x) + logp_\theta(x, z)] \\ = E_{q_\phi(z \mid x)}[-log q_\phi(z \mid x^{(i)}) + log[p_\theta(x \mid z) p_\theta(z)]] \\ = -\int q_\phi(z \mid x)log \frac{q_\phi(z \mid x)}{p_\theta(z)}d\phi + \int q_\phi(z \mid x)log p_\theta(x \mid z)d\phi \\ = -KL(q_\phi(z \mid x) \| p_\theta(z)) + E_{q_\phi(z \mid x)}[log p_\theta(x \mid z)]\]

所以有：

\[logp_\theta(x) = KL(q_\phi(z \arrowvert x)\| p_\theta(z \arrowvert x)) + E_{q_\phi(z \arrowvert x)}[-logq_\phi(z \arrowvert x) + logp_\theta(x, z)] \\ \geq -KL(q_\phi(z \arrowvert x)\|p_\theta(z)) + E_{q_\phi(z \arrowvert x)}[log p_\theta(x \arrowvert z)]\]

$q_\phi(z \arrowvert x)$是Recognition Model，用于去估计后验概率$p_\theta(z \arrowvert x)$ 。假设为高斯隐变量，上面不等式右边的第一项显得微不足道(can be marginalized)， 进而第二项可以通过 Recognition distribution $q_\phi(z \arrowvert x)$估计出来， 经验上高斯隐变量VAE的目标函数为：

\[\tilde L_{VAE}(x; \theta, \phi) = -KL(q_\phi(z \arrowvert x)\|p_\theta(z)) + \frac{1}{L}\sum_{l=1}^{L}log(p_\theta(x \arrowvert z^{(l)}))\]

其中$z = g_\phi(x, \epsilon^{(l)}), \epsilon^{(l)}\thicksim N(0, 1)$， 也就是$z = \epsilon \sigma^2 + \mu$, 其中$\sigma^2$和$\mu$是通过x经过encoder得到的。

识别模型的分布（recognition distribution）$q_\phi(z \arrowvert x)$是输入x重参数化成z的分布，也就是encoder的分布。

$p_\theta(x \arrowvert z^{(l)})$是重参数化z化成x的分布，也就是decoder的分布。

CGM(Deep Conditional Generative Model)

CGM的基本结构

CGM有三种类型的变量：

  • input variables： x
  • output variables： y
  • latent variables: z

其中x和z采样自分布$p(z \arrowvert x)$

y由分布$p(y \arrowvert x, z)$生成

给定x的情况下，产生y时， z可以是很多种形式， 使得CGM模型可以完成一对多的映射关系。

z和x应该是相关的， 然而在实验中， 我们让z和x相互独立，也就是$p_\theta(z \arrowvert x) = p_\theta(z)$

Deep CGMs 通过训练计算条件下的极大似然估计。通常来讲，目标函数是很难处理的，我们使用SGVB框架来训练这个模型。模型的变分下界为：

\[logp_\theta(y \arrowvert x) \geq -KL(q_\phi(z \arrowvert x, y) \| p_\theta(z \arrowvert x)) + E_{q_\phi(z \arrowvert x, y)}[logp_\theta(y \arrowvert x, z)]\]

证明：

在条件VAE中，我们假设要建模的变量为$y$，条件为$x$, 隐变量$z$的近似分布$q_\phi(z \arrowvert x, y)$和真实后验概率$p_\theta(z \arrowvert x, y)$之间的KL-divergence记为：

\[KL[q_\phi(z \arrowvert x, y) \| p_\theta(z \arrowvert x, y)] \\ = \int q_\phi(z \arrowvert x, y) log\frac{q_\phi(z \arrowvert x, y)}{p_\theta(z \arrowvert x, y)}d\phi = \int q_\phi(z \arrowvert x, y)log\frac{q_\phi(z \arrowvert x, y)p_\theta(y \arrowvert x)p_\theta(x)}{p_\theta(z, x, y)}d\phi\]

展开：

\[= \int q_\phi(z \arrowvert x, y)log q_\phi(z \arrowvert x, y)d\phi + \int q_\phi(z \arrowvert x, y)log p_\theta(y \arrowvert x)d\phi + \int q_\phi(z \arrowvert x, y)log p_\theta(x)d\phi - \int q_\phi(z \arrowvert x, y)logp_\theta(z, x, y)d\phi\]

其中，第二项

\[\int q_\phi(z \arrowvert x, y)log p_\theta(y \arrowvert x)d\phi = log p_\theta(y \arrowvert x)\]

其余三项合并，原式：

\[KL[q_\phi(z \arrowvert x, y) \| p_\theta(z \arrowvert x, y)] = log p_\theta(y \arrowvert x) + \int q_\phi(z \arrowvert x, y)log\frac{q_\phi(z \arrowvert x, y)p_\theta(x)}{p_\theta(z, x, y)}d\phi \\ = log p_\theta(y \arrowvert x) + \int q_\phi(z \arrowvert x, y)log\frac{q_\phi(z \arrowvert x, y)}{p_\theta(z, y \arrowvert x)}d\phi \\ = log p_\theta(y \arrowvert x) + \int q_\phi(z \arrowvert x, y)log\frac{q_\phi(z \arrowvert x, y)}{p_\theta(y \arrowvert x, z)p_\theta(z \arrowvert x)}d\phi\]

由于左侧$KL \geq 0$， 因此：

\[logp_\theta(y \arrowvert x) \geq - \int q_\phi(z \arrowvert x, y)log\frac{q_\phi(z \arrowvert x, y)}{p_\theta(y \arrowvert x, z)p_\theta(z \arrowvert x)}d\phi \\ = E_{q_\phi(z \arrowvert x, y)}[log p_\theta(y \arrowvert x, z) + log p_\theta(z \arrowvert x) - q_\phi(z \arrowvert x, y)]d\phi \\ = E_{q_\phi(z \arrowvert x, y)}[log p_\theta(y \arrowvert x, z)] - E_{q_\phi(z \arrowvert x, y)}[log q_\phi(z \arrowvert x, y) - log p_\theta(z \arrowvert x)] \\ = E_{q_\phi(z \arrowvert x, y)}[log p_\theta(y \mid x, z)] - \int q_\phi（z \mid x, y）log \frac{q_\phi(z \mid x, y)}{p_\theta(y \mid x, z)p_\theta(z \mid x)}d\phi \\ = E_{q_\phi(z \mid x, y)}[log p_\theta(y \mid x, z)] - KL[q_\phi(z \mid x, y)\|p_\theta(z \mid x)]\]

左侧$log p_\theta(y \mid x)$是基于条件$x$的后验概率， 右侧是条件VAE的ELBO:

\[ELBO = E_{q_\phi(z \mid x, y)}[log p_\theta(y \mid x, z)] - KL[q_\phi(z \mid x, y)\|p_\theta(z \mid x)]\]

第一项是对隐变量$z \thicksim q_\phi(z \mid x, y)$的期望下的极大似然估计， 第二项是$q_\phi$与先验$p_\theta$的KL约束。

对第一项要通过采样来估计：

\[\tilde L_{CVAE}(x, y; \theta, \phi) = -KL(q_\phi(z \mid x, y)\|p_\theta(z \mid x)) + \frac{1}{L}\sum_{l=1}^{L}log p_\theta(y \mid x, z^{(l)})\]

经验上可以被写为：

\[\tilde L_{CVAE}(x, y; \theta, \phi) = -KL(q_\phi(z \arrowvert x, y) \| p_\theta(z \arrowvert x)) + \frac{1}{L}\sum_{l=1}^{L}logp_\theta(y \arrowvert x, z^{(l)})\]

其中$z^{(l)} = g_\phi(x, y, \epsilon^{(l)}), \epsilon^{(l)} \thicksim N(0, 1)$。

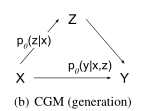
$q_\phi(z \arrowvert x, y)$是一个识别网络（Recognition Network）

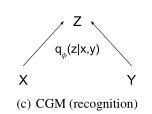
$p_\theta(z \arrowvert x)$是一个条件先验网络（Conditional prior network）

$p_\theta(y \arrowvert x, z)$是一个生成网络（Generation network）

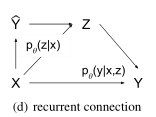
不仅x，还有由CNN预测的$\hat y$也被送进先验网络，在加深卷积结构的同时，这样的一个循环链接被用在结构化输出的预测问题上，通过修正之前的预测去顺序地更新预测。

输出推断和条件概率预测

模型训练好后，我们可以通过CGM的生成过程输入x，得到一个预测y。

为了评估模型结构化输出预测任务， 我们可以通过一个决定性的推断测量预测的准确率：

\[y^* = argmax_y \frac{1}{L} \sum_{l=1}^{L}p_\theta(y \arrowvert x, z^{(l)}), z^{(l)} \thicksim p_\theta(z \arrowvert x)\]

另一种评估CGMs的方式是比较测试集的条件概率。一个直接的方式是，使用先验网络采样z并且求概率的平均值。我们把这种方法叫做蒙特卡罗(Monte Carlo)采样:

\[p_\theta(y \arrowvert x) \approx \frac{1}{S}\sum_{s=1}^{S}p_\theta(y \arrowvert x, z^{(s)}), z^{(s)} \thicksim p_\theta(z \arrowvert x)\]

为了保证准确率， 蒙特卡罗 log-likelihood 估计通常需要大量的采样。

此外，我们通过$q_\phi(z \mid x, y)$采用Importance Sampling(IS)去估计条件概率。

IS的基本原理是：

\[E_{p(a)}[\tau] = E_{p(b)}[\frac{p(a)}{p(b)}\tau]\]

将IS应用到上述采样过程中，更改期望后，需要加入IS weight进行校正：

\[p_\theta(y \arrowvert x) \approx \frac{1}{S}\sum_{1}^{S}\frac{p_\theta(y \arrowvert x, z^{(s)})p_\theta(z^{(s)} \arrowvert x)}{q_\phi(z^{(s)}\arrowvert x, y) }, z^{(s)} \thicksim q_\phi(z \arrowvert x, y)\]

学习预测结构化输出

尽管SGVB学习框架对深度生成模型的训练表现出非常有效，但是在训练时的输出变量的条件自编码器可能不适用于深度条件生成模型(Deep CGMs)在测试时做出预测。换句话说，CVAE在训练时使用识别网络(Recognition Network)$q_\phi(z \mid x, y)$, 但是它使用了先验网络$p_\theta(z \mid x)$在测试集来采样$z$和做一个输出预测。

因为$y$对于识别网络来说是一个输入，对于训练的目标来说可以看作是对$y$的重构， 这相对于预测了来说是个容易的任务。

负的KL散度尽力让两个pipeline接近，一种解决方法是在训练和测试时，给目标函数的KL散度这一项分配更多的权重来减小隐变量的编码的差异， 比如说$-(1 + \beta)KL(q_\phi(z \mid x, y)|p_\theta(z \mid x)) , \beta \geq 0$。

然而，这种方式在实验中并没有效果。

进而我们提出了一种训练网络的方式，在训练和测试时预测的pipeline相一致。

这可以通过使识别网络(Recognition Network)和先验网络(Prior Network)相同， 比如：

\[q_\phi(z \mid x, y) = p_\theta(z \mid x)\]

然后我们得到了如下的目标函数：

\[\tilde L_{GSNN}(x, y; \theta, \phi) = \frac{1}{L} \sum_{l=1}^{L} log p_\theta(y \mid x, z^{(l)}) \text {, where $z^{l} = g_\theta(x, \epsilon^{(l)})$, $\epsilon^{(l)} \thicksim N(0, 1)$}\]

我们把这个模型叫做Gaussian Stochastic Neura Network(GSNN)。 注意GSNN可以通过让CVAE的识别网络和先验网络相等得到。 因此， 学习的技巧， 比如CVAE的重参数化可以用在GSNN的训练上。

同样的，推断和条件概率的估计和CVAE相同。

最终我们得到的目标函数如下：

\[\tilde L_{hybrid} = \alpha \tilde L_{CVAE} + (1 - \alpha) \tilde L_{GSNN}\]

其中$\alpha$用来平衡两个目标

当$\alpha = 1$时，我们重现了CVAE的目标

当$\alpha = 0$时， 训练的模型仅仅是没有识别网络的GSNN

实现部分

引入相关包

1
2
3
4
5
6
7
8
9
10
11
12

import os
import time
import torch
import torch.nn as nn
import argparse
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from torchvision import transforms
from torchvision.datasets import MNIST
from torch.utils.data import DataLoader
from collections import defaultdict

参数初始化

1
2
3
4
5
6
7
8
9
10
11
12
13

parser = argparse.ArgumentParser()
parser.add_argument("--seed", type=int, default=0)
parser.add_argument("--epochs", type=int, default=10)
parser.add_argument("--batch_size", type=int, default=64)
parser.add_argument("--learning_rate", type=float, default=0.001)
parser.add_argument("--encoder_layer_sizes", type=list, default=[784, 256])
parser.add_argument("--decoder_layer_sizes", type=list, default=[256, 784])
parser.add_argument("--latent_size", type=int, default=2)
parser.add_argument("--print_every", type=int, default=100)
parser.add_argument("--fig_root", type=str, default='figs')
parser.add_argument("--conditional", default=True, action='store_true')

args = parser.parse_known_args()[0]

索引转独热

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

def idx2onehot(idx, n):
    # idx = y， 是label
    # n = 10. 因为label范围是0~9
    assert torch.max(idx).item() < n
    if idx.dim() == 1:
        # shape从[64]的list变成[64,1]
        idx = idx.unsqueeze(1)

    # shape: [64, 10]
    onehot = torch.zeros(idx.size(0), n)
    # 按行填充
    # idx: shape为[64, 1]的0~9的阵
    # 按idx的index填1
    onehot.scatter_(1, idx, 1)

    return onehot

将label转换成独热型的矩阵

将64x1的label

变成64 x 10的独热

VAE模型

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

class VAE(nn.Module):

    def __init__(self, encoder_layer_sizes, latent_size, decoder_layer_sizes,
                 conditional=False, num_labels=0):

        super().__init__()

        if conditional:
            assert num_labels > 0

        assert type(encoder_layer_sizes) == list
        assert type(latent_size) == int
        assert type(decoder_layer_sizes) == list

        self.latent_size = latent_size

        self.encoder = Encoder(
            encoder_layer_sizes, latent_size, conditional, num_labels)
        self.decoder = Decoder(
            decoder_layer_sizes, latent_size, conditional, num_labels)

    def forward(self, x, c=None):

        if x.dim() > 2:
            # x shape: [64, 784]
            x = x.view(-1, 28*28)
        
        # batch_size: 64
        batch_size = x.size(0)
        # encoder 
        means, log_var = self.encoder(x, c)
        # reparameter: q_\phi(z|x, y)
        std = torch.exp(0.5 * log_var)
        # eps shape: [64, 2]
        eps = torch.randn([batch_size, self.latent_size]).cuda()
        # std shape: [64, 2]
        z = eps * std + means
        # decoder: p(x|z, y)
        recon_x = self.decoder(z, c)

        return recon_x, means, log_var, z

    def inference(self, n=1, c=None):
        # p_theta(z)
        batch_size = n
        # 假设z是x encode过来的, 即p_\theta(z|x，y)
        # 那么这里就是假设p_theta(z|x)为标准正态分布
        # 可以推得p_theta(x)为标准正态分布
        z = torch.randn([batch_size, self.latent_size]).cuda()

        # p_\theta(x|z, y)
        recon_x = self.decoder(z, c)

        return recon_x

编码器

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

class Encoder(nn.Module):

    def __init__(self, layer_sizes, latent_size, conditional, num_labels):

        super().__init__()

        self.conditional = conditional
        if self.conditional:
            # layer_size :　［794, 256］
            layer_sizes[0] += num_labels
            print("encoder layer_size: " + str(layer_sizes[0]))

        self.MLP = nn.Sequential()
        # layer_size[:-1]: [794] 
        # layer_size[1:]：[256]　
        # zip: [(794, 256)]
        for i, (in_size, out_size) in enumerate(zip(layer_sizes[:-1], layer_sizes[1:])):
            self.MLP.add_module(
                name="L{:d}".format(i), module=nn.Linear(in_size, out_size))
            self.MLP.add_module(name="A{:d}".format(i), module=nn.ReLU())

        # layer_sizes[-1] : 256
        self.linear_means = nn.Linear(layer_sizes[-1], latent_size)
        self.linear_log_var = nn.Linear(layer_sizes[-1], latent_size)

    def forward(self, x, c=None):

        if self.conditional:
            #c = y， 是label
            # 转换之后c的shape: [64, 10]
            c = idx2onehot(c.cpu(), n=10).to(device)
            # 拼接后x的shape：[64, 794]
            x = torch.cat((x, c), dim=-1).to(device)

        # x shape:[64, 256]
        x = self.MLP(x)

        # means shape: [64, 2]
        means = self.linear_means(x)
        # log_vars shape: [64, 2]
        log_vars = self.linear_log_var(x)

        return means, log_vars

解码器

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

class Decoder(nn.Module):

    def __init__(self, layer_sizes, latent_size, conditional, num_labels):

        super().__init__()

        self.MLP = nn.Sequential()

        self.conditional = conditional
        if self.conditional:
            input_size = latent_size + num_labels
        else:
            input_size = latent_size

        # layer_size: [256, 784]
        # layer_size[:-1]:256
        # zip : [(12, 256), (256, 784)]
        for i, (in_size, out_size) in enumerate(zip([input_size]+layer_sizes[:-1], layer_sizes)):
            self.MLP.add_module(
                name="L{:d}".format(i), module=nn.Linear(in_size, out_size))
            if i+1 < len(layer_sizes):
                self.MLP.add_module(name="A{:d}".format(i), module=nn.ReLU())
            else:
                self.MLP.add_module(name="sigmoid", module=nn.Sigmoid())

    def forward(self, z, c):

        if self.conditional:  
            c = idx2onehot(c.cpu(), n=10).to(device)
            z = torch.cat((z, c), dim=-1).to(device)

        x = self.MLP(z)

        return x

加载模型数据集及优化器初始化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

torch.manual_seed(args.seed)
if torch.cuda.is_available():
    torch.cuda.manual_seed(args.seed)

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')

ts = time.time()

dataset = MNIST(
    root='../data', train=True, transform=transforms.ToTensor(),
    download=True)
data_loader = DataLoader(
    dataset=dataset, batch_size=args.batch_size, shuffle=True)

def loss_fn(recon_x, x, mean, log_var):
    # recon_x: q_\phi(x|z, y)
    # x: p_\theta(x|z, y) = p_\theta(x) 为标准正态分布
    # 为什么论文里写的是p_\theta(y|x, z), z服从q_\phi(z|x, y)
    # 这里算的是p_\theta(x|z, y), z服从q_\phi(z|x, y)
    # 可以理解为算出recon_x 里包含了y？
    BCE = torch.nn.functional.binary_cross_entropy(
        recon_x.view(-1, 28*28), x.view(-1, 28*28), reduction='sum')
    # DKL(q_\phi(z|x, y)||p(z|y))
    KLD = -0.5 * torch.sum(1 + log_var - mean.pow(2) - log_var.exp())

    return (BCE + KLD) / x.size(0)

vae = VAE(
    encoder_layer_sizes=args.encoder_layer_sizes,
    latent_size=args.latent_size,
    decoder_layer_sizes=args.decoder_layer_sizes,
    conditional=args.conditional,
    num_labels=10 if args.conditional else 0).to(device)

optimizer = torch.optim.Adam(vae.parameters(), lr=args.learning_rate)

logs = defaultdict(list)

训练

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68

for epoch in range(args.epochs):

    tracker_epoch = defaultdict(lambda: defaultdict(dict))

    for iteration, (x, y) in enumerate(data_loader):

        x, y = x.to(device), y.to(device)

        if args.conditional:
            recon_x, mean, log_var, z = vae(x, y)
        else:
            recon_x, mean, log_var, z = vae(x)

        for i, yi in enumerate(y):
            id = len(tracker_epoch)
            tracker_epoch[id]['x'] = z[i, 0].item()
            tracker_epoch[id]['y'] = z[i, 1].item()
            tracker_epoch[id]['label'] = yi.item()

        loss = loss_fn(recon_x, x, mean, log_var)

        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

        logs['loss'].append(loss.item())

        if iteration % args.print_every == 0 or iteration == len(data_loader)-1:
            print("Epoch {:02d}/{:02d} Batch {:04d}/{:d}, Loss {:9.4f}".format(
                epoch, args.epochs, iteration, len(data_loader)-1, loss.item()))

            if args.conditional:
                c = torch.arange(0, 10).long().unsqueeze(1)
                x = vae.inference(n=c.size(0), c=c)
            else:
                x = vae.inference(n=10)

            plt.figure()
            plt.figure(figsize=(5, 10))
            for p in range(10):
                plt.subplot(5, 2, p+1)
                if args.conditional:
                    plt.text(
                        0, 0, "c={:d}".format(c[p].item()), color='black',
                        backgroundcolor='white', fontsize=8)
                x = x.cpu()
                plt.imshow(x[p].view(28, 28).data.numpy())
                plt.axis('off')

            if not os.path.exists(os.path.join(args.fig_root, str(ts))):
                if not(os.path.exists(os.path.join(args.fig_root))):
                    os.mkdir(os.path.join(args.fig_root))
                os.mkdir(os.path.join(args.fig_root, str(ts)))

            plt.savefig(
                os.path.join(args.fig_root, str(ts),
                             "E{:d}I{:d}.png".format(epoch, iteration)),
                dpi=300)
            plt.clf()
            plt.close('all')

    df = pd.DataFrame.from_dict(tracker_epoch, orient='index')
    g = sns.lmplot(
        x='x', y='y', hue='label', data=df.groupby('label').head(100),
        fit_reg=False, legend=True)
    g.savefig(os.path.join(
        args.fig_root, str(ts), "E{:d}-Dist.png".format(epoch)),
        dpi=300)

实验结果

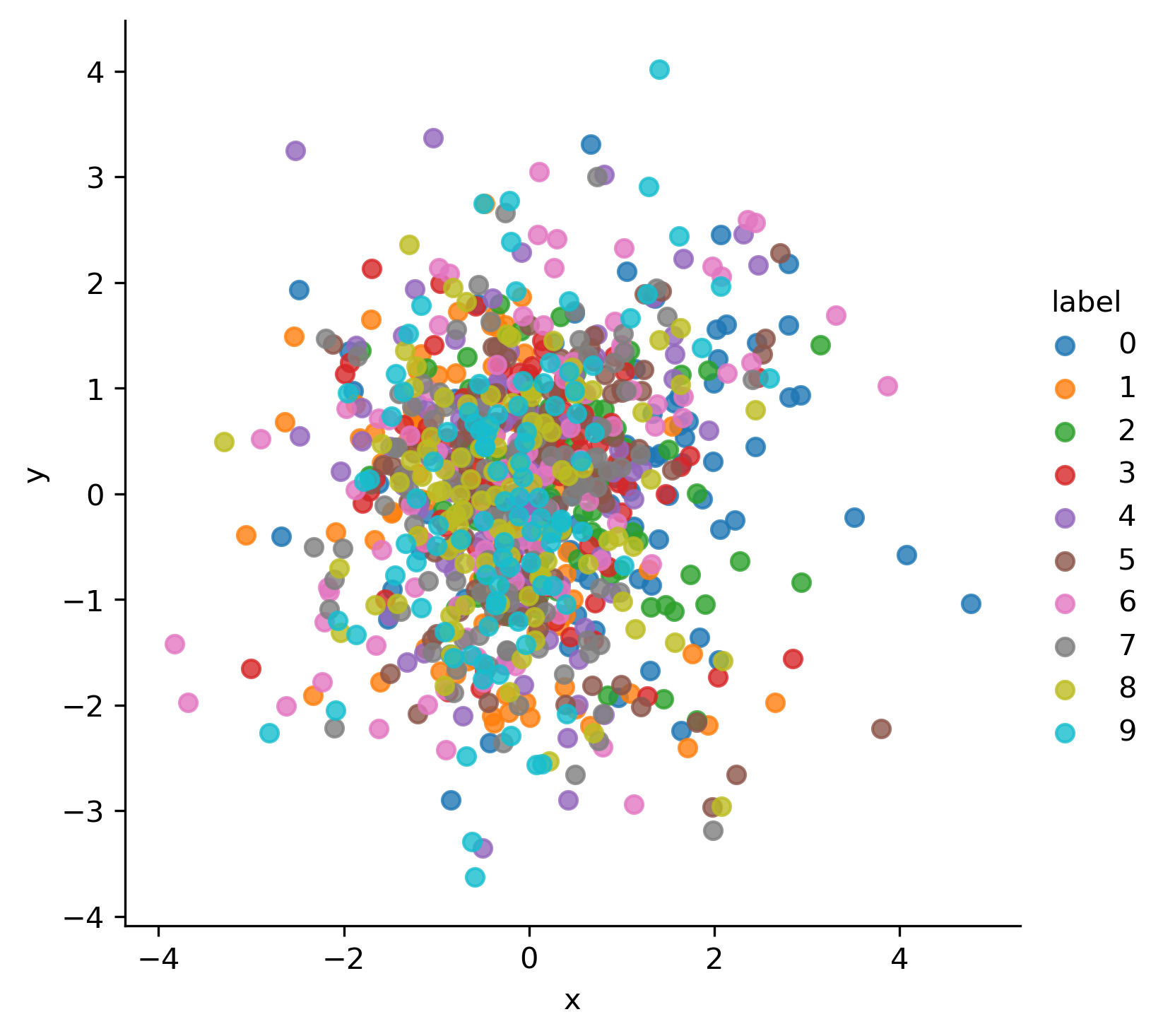
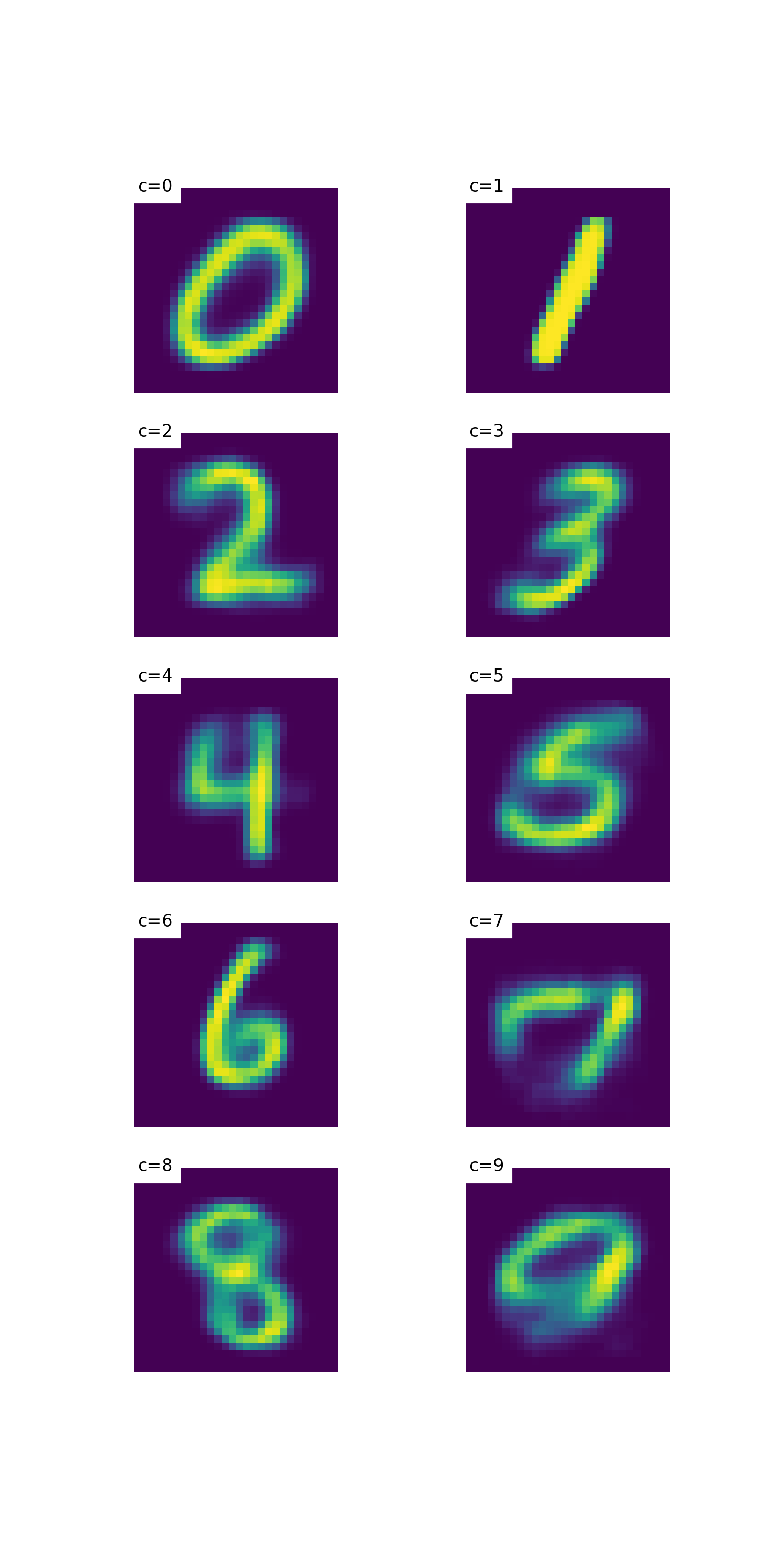
Reference

  1. Sohn K, Lee H, Yan X. Learning structured output representation using deep conditional generative models[C]//Advances in neural information processing systems. 2015: 3483-3491.
  2. Conditional VAE
  3. timbmg/VAE-CVAE-MNIST
CATALOG
    FEATURED TAGS
    mark 深度学习 机器学习 HSI Detection d2l Geek GAN 课业笔记 Diffusion CVPR 2023 Research & Writing low-level CV CVPR 2022 ICCV 2023 Scene Graph CV ECCV 2022 NLP MMML Backbone Arxiv 2022 NIPS 2022 CVPR 2020 NIPS 2021 Segmentation GNN & GCN 计算方法 CVPR 2018 CVPR 2021 ECCV 2020 ICCV 2019 强化学习 FastAI arXiv 2023 凸优化 操作系统 数据结构 矩阵论 离散数学 计算机网络 Arxiv 2021 CVPR 2019 ICCV 2021 OpenCV VAE Arxiv 2020 Arxiv 2023 CVPR 2017 ICCV 2017 ICLR 2021 Life TPAMI 2023 学会理财 嵌入式 生活 算法 计算智能 CVPR 2016 CVPRW 2022 CVPRW 2023 Docker ICLR 2022 MMLab Python Research & Competition TGRS 2023 TIP 2013 TIP 2021 TMM 2023 TPAMI 2017 TPAMI 2019 TPAMI 2022 WACV 2024
    FRIENDS