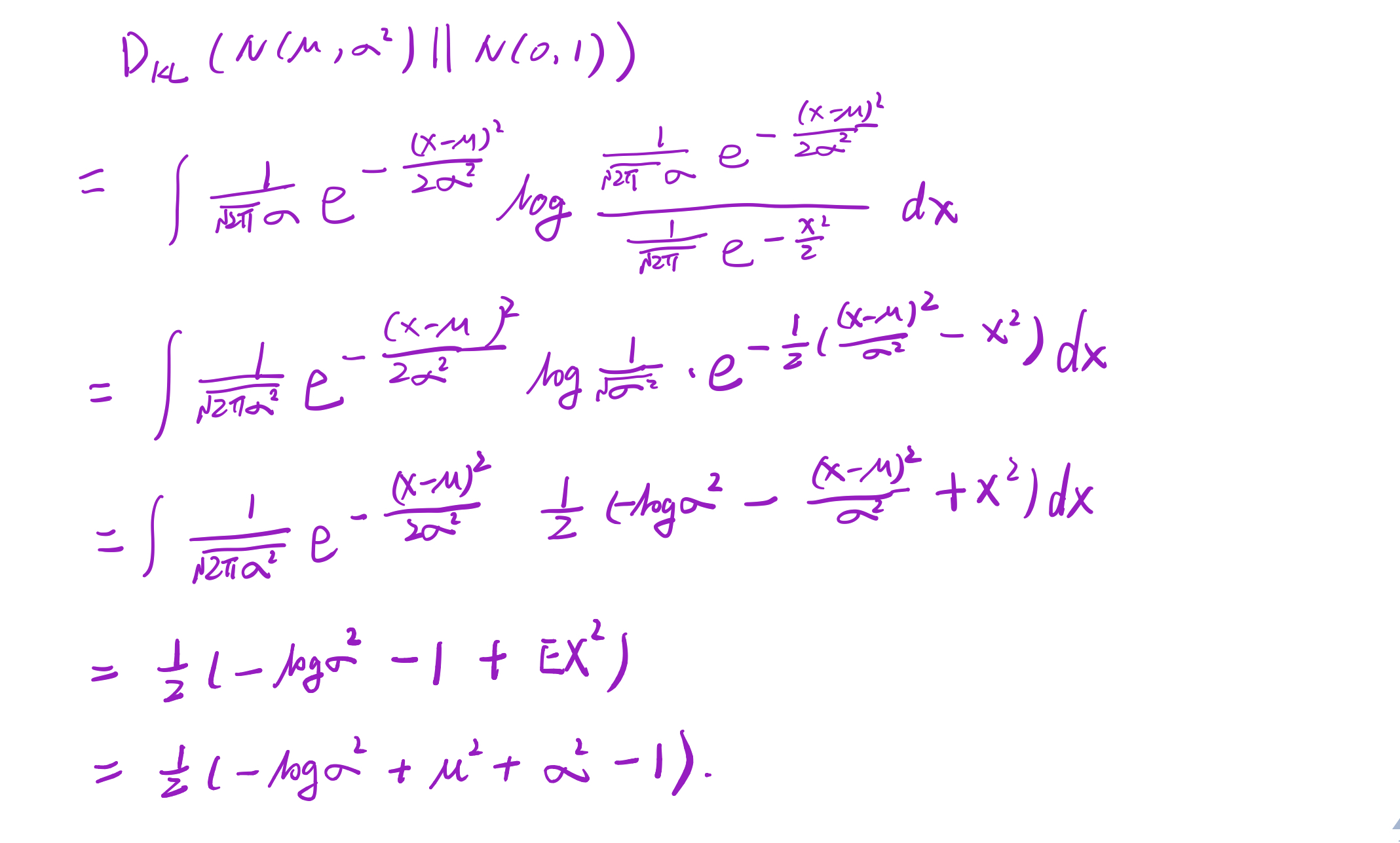VAEs相关理论
变分下限
变分推断(variational inference)常用方法时求观察量x的似然函数:
\[log p_\theta(x_1, ..., x_n) = \sum_{i=1}^{n} log p(x_{i})\]可以化成(推导1):
\[log p_\theta(x_i) = D_{KL}(q_\phi(z \mid x_i)\|p_\theta(z \mid x_i)) + L\]第一项KL散度大于0, 第二项L函数就是变分下限:
\[L = E_{q_\phi(z \mid x_i)}[log p_\theta(x_i, z) - log (q_phi(z \mid x_i))]\]也可以写成如下(推导2):
\[L = -D_{KL}(q_\phi(z \mid x_i)\|p_\theta(z)) + E_{q_\phi(z \mid x_i)}[log p_\theta(x_i \mid z)]\]其中第一项可以通过分解得到(推导3):
\[-D_{KL}(q_\phi(z \mid x_i)\|p_\theta(z)) = \frac{1}{2}(1+log \sigma^2 - \mu^2 - \sigma^2)\]其中$p_\theta(z)$其实是由encoder得到的,即$p_\theta(z) = p_\theta(z \mid x)$
而在整个VAE模型中,我们并没有使用$p_\theta(z)$是正态分布的假设,我们用的是假设$p_\theta(z \mid x)$是正态分布:
\[p(z) = \sum_x p(z \mid x)p(x) = \sum_x N(0, 1)p(x) = N(0, 1)\sum_x p(x) = N(0, 1)\]对于第二项,使用蒙特卡洛(MC)算法, 即:
\[E_{q_\phi(z \mid x_i)}[log p_\theta(x_i \mid z)] = \sum_{i=1}^{n}q_\phi(z \mid x_i)log p_\theta(x_i \mid z) \approx \frac{1}{L} \sum_L log p(x_i \mid z_l)\]其中:
\[z_l \thicksim q_\phi(z \mid x)\]思考:为什么代码实现时,第二部分计算的是交叉熵,且label是真实数据?
第一项实际上是一个重建error,为什么?好,我们说从 $z$ 到 $\hat x$ 的转换是神经网络干的事情,它是一个函数,虽然说我们不知道它具体的表达式是什么,无论我输入一个怎样的input,总是会给我一个相同的output,所以 $(I)$ 式的第一项中的 $log p(x \mid z)$ 可以看作是 $log p(x \mid \hat x)$ ,假设p是一个正态分布,你自己想想会是什么!$L_2$ loss!当然,如果你假设p是伯努利分布,那就是交叉熵了。
VAEs公式推导
变分下限
推导1:
\[log p(x) = \sum_z q(z \mid x)log p(x) \\ = \sum_z q(z \mid x)log (\frac{p(z, x)}{p(z \mid x)}) \\ = \sum_z q(z \mid x)log (\frac{p(z, x)}{q(z \mid x)} \frac{q(z \mid x)}{p(z \mid x)}) \\ = \sum_z q(z \mid x) log (\frac{p(z, x)}{q(z \mid x)}) + \sum_z q(z \mid x)log (\frac{q(z \mid x)}{p(z \mid x)}) \\ = L + D_{KL}(q(z \mid x) \| p(z \mid x))\]推导2:
\[L = E_{q_\phi(z \mid x)}[log p_\theta(x, z) - log (q_\phi(z \mid x))] \\ = \sum_z q_\phi(z \mid x)log p_\theta(x, z) - \sum_z q_\phi(z \mid x)log q_\phi(z \mid x) \\ = \sum_z q_\phi(z \mid x)log p_\theta(x, z) - \sum_z q_\phi(z \mid x)log \frac{q_\phi(z \mid x)}{p_\theta(z)} - \sum_z q_\phi(z \mid x)log p_\theta(z) \\ = \sum_z q_\phi(z \mid x)log \frac{p_\theta(x, z)}{p_\theta(z)}- \sum_z q_\phi(z \mid x)log \frac{q_\phi(z \mid x)}{p_\theta(z)} \\ = \sum_z q_\phi(z|x)log p(x \mid z) - D_{KL}(q_\phi(z \mid x)\|p_\theta(z)) \\ = E_{q_\phi(z \mid x)}[log p(x \mid z)] - D_{KL}(q_\phi(z \mid x)\|p_\theta(z))\]推导3:
\[D_{KL}(q_\phi(z \mid x) \| p_\theta(z)) = \sum q_\phi(z \mid x) log \frac{q_\phi(z \mid x)}{p_\theta(z)} \\\]其中$q_\phi(z \mid x) \thicksim N(\mu, \sigma^2)$, $p_\theta(z) \thicksim N(0, 1)$