谓词
个体:命题中所涉及的对象。
谓词: 刻画个体的性质或若干个体间关系的模式。 一般用大写字母P, Q, R, … 表示。
例子:
张明生于背景。
Q(x, y): x生于y; c:张明, d:北京, 则有Q(c, d)
个体变元:讨论对象未确定, 泛指的个体, 如x, y。
个体常元:讨论对象已确定,特定的个体,如c,d。
个体域:n元谓词P(x1, x2, … , xn)中个体变元的取值范围叫做论述域或个体域。可有限也可无限。
Note:
- 一元谓词刻画性质,多元谓词刻画关系。
- 多元谓词中注意个体变元的次序。
- 命题可以认为是0元谓词,所以谓词是命题的扩充,命题是谓词的一种特殊情况。
简单命题函数(简单谓词命名式):由一个谓词,一些个体变元组成的表达式
复合命题函数(复合谓词命名式):由一个或n个简单命题函数以及逻辑联结词组成的表达式
逻辑连接词就是命题联结词
量词
- 全称量词:$\forall$
- 存在量词:$\exists$
在谓词前面加上全称量词或存在量词,说成是变元x被全称量化或存在量化。量化用来约束变元。
使$P(x_1, x_2, …, x_n)$成为命题的两种方法:
- 所有个体变元指定确定的个体
- 将所有个体变元量化
例子: P(x)表示“x是质数”, x是自然数。
$\forall x, P(x)$和$\exists x, P(x)$是命题
P(x): x是质数; a:3, 则有P(a)为命题。
全总个体域:将谓词中各个体变元的所有个体域统一起来,称为全总个体域。
特性谓词:(全总个体域中)限定个体变化范围的谓词。
特性谓词加入断言的规则:
- 全称量词,特性谓词作为蕴含式的前件加入
- 存在量词,特性谓词作为合取项加入
谓词演算公式与翻译
谓词演算公式
谓词演算的原子公式:不出现命题联结词和量词的谓词命名式$P(x_1,x_2,… ,x_n)$
谓词演算的合式公式:
- 谓词演算的原子公式是谓词演算公式;
- 若A,B是谓词演算公式,则$(\lnot A),(A \land B),(A \lor B), (A→B),(A \leftrightarrow B),\forall x \quad A,\exists x \quad A$是谓词演算公式
- 只有有限次应用上述步骤构成的公式才是谓词演算公式
翻译
\[\lnot \forall x (R(x) \rightarrow Q(x))\]并非每个实数都是有理数。 (R, Q)
\[\forall x (M(x) \rightarrow \exists y (G(y) \land F(x, y)))\]每个人都有些缺点。(M, G, F)
思考:怎么理解?
论述域是人和缺点, M(x)表示“x是人”, G(y)表示“y是缺点”, F(x, y)表示“x有y”。
\[\exists x (M(x) \land F(x)) \land \lnot \forall x(M(x) \rightarrow F(x))\]尽管有人聪明, 但未必所有人都聪明。(M, F)
论述域是人, M(x)表示“x是人”, F(x)表示“x聪明”。
自由变元与约束变元
辖域:紧接于量词之后最小的子公式叫量词的辖域
例子:
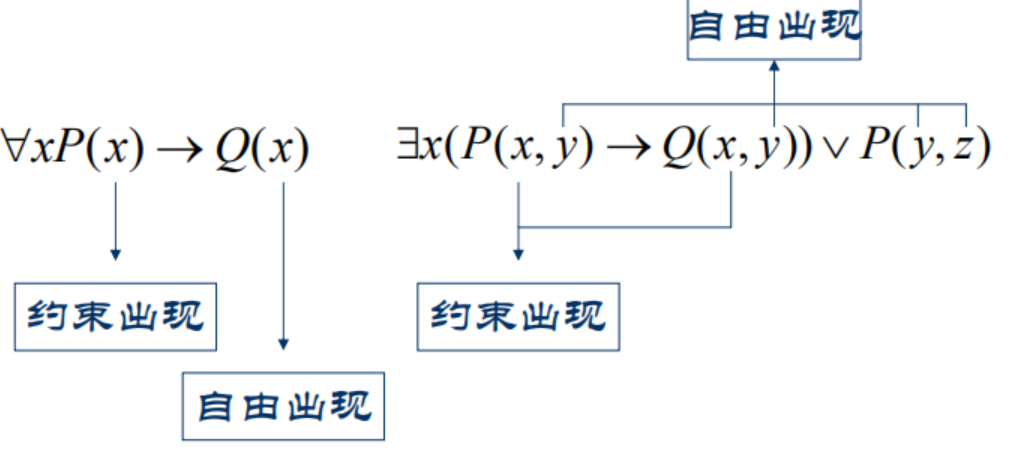
\[\forall x \underline {P(x)} \rightarrow Q(x)\] \[\exists x \underline {(P(x, y) \land Q(x, y))} \rightarrow F(x)\]注意:辖域若不是原子公式,两边要有括号; 否则, 不应有括号。
约束变元:在量词$\forall x ,\exists x$的辖域内变元x的一切出现称为约束出现
自由变元:在一公式中,变元的非约束出现称为变元的自由出现
谓词演算
谓词演算的基本概念
定义1:两个任意谓词公式A和B,E是它们公有的论述域,若:
- 对公式A和B中的谓词变元(包括命题变元),指派以任一在E上有意义的确定的谓词。
- 对谓词命名式中的个体变元,指派以E中的任一确定的个体。
所得的命题具有同样的真值,则称公式A和B遍及E等价,记为在E上$A \Leftrightarrow B$
思考:谓词变元和命题变元有什么区别?
回答:
首先什么是命题, 具有确定真值的陈述句。什么是命题变元, 一个命题标识符表示任意的命题。
其次什么是谓词,刻画个体的性质或若干个体间关系的模式。什么是谓词变元,谓词变元指的是数理逻辑中表示某一范围内的任意谓词。
定义2:如果两谓词公式A和B,在任意论述域上都等价,则称A和B等价,记为$A \Leftrightarrow B$
定义3:给定任一谓词公式A,如果在论述域E上,对公式A中的谓词和个体变元进行定义1中的两种指派,所得命题:
- 都真,则称A在E上有效或在E上永真。
- 至少有一个是真,则称A在E上可满足。
- 都假,则称A在E上永假或在E上不可满足。
定义4:给定任一谓词公式A,如果在任意论述域上,对公式A中的谓词和个体变元进行定义1中的两种指派,所得命题:
- 都真,则称A有效或永真。
- 至少有一个是真,则称A可满足。
- 都假,则称A永假或不可满足。
定义5:设A、B是谓词公式,E是它们共同的个体域,如果A→B在E上永真,则称在E上A蕴含B,记作在E上$A \Rightarrow B$。
定义6:如果两谓词A和B,在任意论述域上A都蕴含B,则称A蕴含B,记为$A \Rightarrow B$。
思考:谓词和谓词公式有什么区别?
回答:
谓词:刻画个体的性质或若干个体间关系的模式。
谓词公式:
- 单个谓词是谓词公式,称为原子谓词公式
- 若A是谓词公式,则¬A $\lnot$ A¬A也是谓词公式
- 若A,B都是谓词公式,则A∧B,A∨B,A→BA $\land$ B, A $\lor$ B, A $\to$ BA∧B,A∨B,A→B也都是谓词公式
- 若A是谓词公式,则(∀X)A,(∃X)A($\forall$ X)A,($\exists$ X)A(∀X)A,(∃X)A也都是谓词公式
- 有限步应用1~4步所得到的公式也是谓词公式
判断谓词公式永真-真值表方法
例子:
P(x)仅可解释为: a. A(x): x是质数。 b. B(x):x是合数。 论述域是{3, 4}, 判定谓词公式$P(x) \land \exists x P(x)$是否永真。
| P(x) | x | $P(x) \land \exists x P(x)$ |
|---|---|---|
| A(X) | 3 | $1 \land 1 \Leftrightarrow 1$ |
| A(X) | 4 | $0 \land 1 \Leftrightarrow 0$ |
| B(X) | 3 | $0 \land 1 \Leftrightarrow 0$ |
| B(X) | 4 | $1 \land 1 \Leftrightarrow 1$ |
谓词演算的基本永真公式
命题演算的永真公式也是谓词演算的永真公式。
谓词演算是命题演算的扩充
思考:这里的例子不明白。
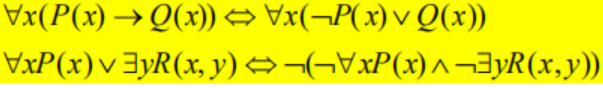
回答:
利用公式
\[P \rightarrow Q \Leftrightarrow \lnot P \lor Q\]推导
量词的添加与消去
如果A是不含约束变元x的公式,则
\[\forall x A \Leftrightarrow A \quad \exists x A \Leftrightarrow A\]思考:这里的例子也不明白。

量词的否定
否定联结词可以通过量词深入到辖域,反之亦可。
\[\lnot \forall x P(x) \Leftrightarrow \exists \lnot P(x)\] \[\lnot \exists x P(x) \Leftrightarrow \forall \lnot P(x)\]否定的深入:
\[\lnot \forall x \forall y \exists z (x + z = y) \\ \Leftrightarrow \exists x \lnot \forall y \exists z (x + z = y) \\ \Leftrightarrow \exists x \exists y \lnot \exists z (x + z = y) \\ \Leftrightarrow \exists x \exists y \forall z \lnot (x + z = y) \\ \Leftrightarrow \exists x \exists y \forall z (x + z \neq y)\]量词辖域的扩张和收缩
\[\forall x (A(x) \lor B) \Leftrightarrow \forall x A(x) \lor B \\ \forall x (A(x) \land B) \Leftrightarrow \forall x A(x) \land B \\ \exists x (A(x) \lor B) \Leftrightarrow \exists x A(x) \lor B \\ \exists x (A(x) \land B) \Leftrightarrow \exists x A(x) \land B\]这里B是不含约束变元x的谓词(包括命题),所以它属于或不属于量词的辖域均有同等意义。
量词的分配形式
\[\forall x (A(x) \land B(x)) \Leftrightarrow \forall x A(x) \land \forall x B(x) \\ \exists x (A(x) \lor B(x)) \Leftrightarrow \exists x A(x) \lor \exists x B(x) \\ \exists x (A(x) \land B(x)) \Rightarrow \exists x A(x) \land \exists x B(x) \\ \forall x A(x) \lor \forall x B(x) \Rightarrow \forall x (A(x) \lor B(x))\]量词对条件和双条件的处理
利用公式
\[P \rightarrow Q \Leftrightarrow \lnot P \lor Q\]以及CP规则进行推导
思考: 怎么理解这个公式?
回答: 列出真值表:
| $P$ | $Q$ | $P \rightarrow Q$ | $\lnot P \lor Q$ |
|---|---|---|---|
| 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
思考:什么是CP规则?
回答:
前提是H1,H2,…,Hn,欲证结论R→P(结论是条件式),则将条件式作为附加前提证得P即可,这就是CP规则。
设H=H1∧H2∧…∧Hn,由前提H证明R→P,即证明H→(R→P)永真,而H→(R→P)等价于H∧R→P,因此证明H∧R→P永真即可。
\[\forall x (A(x) \rightarrow B(x)) \Rightarrow \forall A(x) \rightarrow \forall B(x) \\ \exists x (A(x) \rightarrow B(x)) \Leftrightarrow \exists x A(x) \rightarrow x B(x) \\ \exists x A(x) \rightarrow \forall x B(x) \Rightarrow \forall x (A(x) \rightarrow B(x)) \\ \forall x(A(x) \leftrightarrow B(x)) \Rightarrow \forall x A(x) \leftrightarrow \forall x B(x)\]谓词演算的推理规则
命题演算中所有推理规则在谓词演算中都适用
谓词演算中所有永真蕴含式和等价式也可使用
思考:什么是永真蕴含式?
回答:
首先什么是蕴含式。
设p、q为两个命题。复合命题”如果p,则q”称为p与q的蕴含式,记作p→q。并称p为蕴含式的前件,q为后件。并规定p→q为假当且仅当p为真q为假。
所以永真蕴含式就是永真的蕴含式
全称指定规则(Universal Specification,US )
\[\frac{\forall x P(x)}{\therefore P(c)}\]P是谓词, c是论述域中任意个体。 意义是, 全程量词可以删除。
存在指定规则(Existential Specification,ES )
\[\frac{\exists x P(x)}{\therefore P(c)}\]P是谓词, c是论述域中某些个体, 不是任意的。
全称推广规则(Universal Generalization,UG)
\[\frac{P(x)}{\therefore \forall x P(x)}\]如果能够证明对于论述域中每一个个体x使P(x)都成立, 则可以得到上面结论。
存在推广规则(Existential Generalization,EG)
\[\frac{P(c)}{\therefore \exists x P(x)}\]p是谓词, c是论述域中一个个体。意义是, 对论述域中某些个体使P(x)为真, 则可得上面结论。