【Geek之路】《剑指offer》思路及代码合集

Posted by ShawnD on February 24, 2020

1. 二维数组中的查找

看到这个题目的第一想法，就是二分查找。

然而在本地调试通过后在牛客上不通过

百度了一下段错误的定义 所谓的段错误 就是指访问的内存超出了系统所给这个程序的内存空间 大概是超出了程序的内存空间大小。这道题要求内存空间为32768K

二分查找的方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

class Solution {
public:
    bool Find(int target, vector<vector<int> > array) {
        for(vector<vector<int> >::iterator it=array.begin();it<array.end();++it)
        {
            if(Binary_Search(target, *it)) return true;
        }
        return false;
    }
    bool Binary_Search(int target, vector<int> a){
        int l = a.front(), r = a.back();
        int mid;
        while(l<=r){
            mid = l + (r - l) / 2;
            if(a[mid] == target) return true;
            if(a[mid] < target){
                l = mid + 1;
            }else{
                r = mid - 1;
            }
        }
        return false;
    }
};

然后使用暴力遍历查找的方法， AC：

1
2
3
4
5
6
7
8
9
10
11
12
13

class Solution_1 {
public:
    bool Find(int target, vector<vector<int> > array) {
        for(vector<vector<int> >::iterator it=array.begin();it<array.end();++it)
        {
            for(int i=0; i<(*it).size(); ++i)
            {
                if(target == (*it)[i]) return true;
            }
        }
        return false;
    }
};

2. 替换空格

算法分为两部分：

  • 检测空格，将空格后的字符后移两位
  • 将空格及其后两个的位置替换

一开始做考虑数组的大小问题

遇到了realloc和静态数组的问题。

新分配在堆内的内存,数组定义之后不能改变大小，realloc(p,sizeof(p)+sizeof(int))函数不会改变p的值，新的内存地址是函数的返回值。

realloc只能给动态数组重新分配大小。

后来发现题目并不需要考虑数组大小的问题， 很容易就解决了

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

class Solution {
public:
	void replaceSpace(char *str,int length) {
	    for(int i=0; i<length; ++i){
            if(str[i] == ' '){
                houyi(str, length, i);
                length += 2;
                str[i] = '%';
                str[i+1] = '2';
                str[i+2] = '0';
            }
	    }

	}
	void houyi(char *str, int length, int pos){
	    char *p1, *p2;
	    length += 2;
	    p1 = str + length - 1;
	    p2 = str + length - 3;
	    for(int i=pos+3; i<length; ++i){
            *p1 = *p2;
            --p2;
            --p1;
	    }

	}
};

3. 从尾到头打印链表

这道题很简单，将单链表头插法逆序，然后顺序将val存入vector即可。

一开始不知道单链表是否带有头结点， 经测试，单链表为不带头结点的单链表。

这道题解决长久以来多级指针， 以及指针的引用上的困惑。

长久以来，我对指针的理解都是 多一个 * 就是深一级的地址。

我都是将 “ *变量名称” 理解为一个整体， 事实上这样理解很容易把自己整懵。

如果将 “数据类型*” 理解为一个整体，这就是一个地址， 每多一个 *， 那么地址就深一级， 而变量就是指代这个深一级的地址， 这样就会好理解很多。

将这个多级指针视作一个变量后， 就很容易理解指针的引用了。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

class Solution {
public:
    // 经测试，链表为不带头节点的单链表
    // 将链表使用头插法逆置，再将val顺序存入vector
    vector<int> printListFromTailToHead(ListNode* head) {

        vector<int> buffer;
        if(!head) return buffer;

        ListNode* H = (ListNode*)malloc(sizeof(ListNode));
        H->next = head;
        ListNode* p = H->next;
        ListNode* r;

        H->next = NULL;
        while(p){
            r = p->next;
            p->next = H->next;
            H->next = p;
            p = r;

        }
        p = H->next;
        while(p){
            buffer.push_back(p->val);
            p = p->next;
        }
        delete H;
        return buffer;

    }

    void CreateLinkList(ListNode* &L, int n){
        ListNode* H = (ListNode*)malloc(sizeof(ListNode));
        H->next = NULL;
        ListNode *p;
        for(int i=0; i<n; ++i){
            p = (ListNode*)malloc(sizeof(ListNode));
            p->next = H->next;
            p->val = i;
            H->next = p;
        }
        L = H->next;
    }

    void printList(ListNode* &L){
        ListNode *p = L;
        while(p!=NULL){
            cout << p->val << ' ';
            p = p->next;
        }
        cout << endl;
    }
};

4. 重建二叉树

这个题想起来很容易，尤其是手动模拟，简直是送分题。

但是如果要用代码实现，就需要编程的思维，每一步都要非常清楚，写起来还是有点麻烦的。

通过这道题，理解了以下vector赋值的方式，原理上是如何赋值的

// 这种方式得到的是两个地址之间截到的的变量 vector<int> test = vector<int>(vin.begin(), vin.begin()+1);

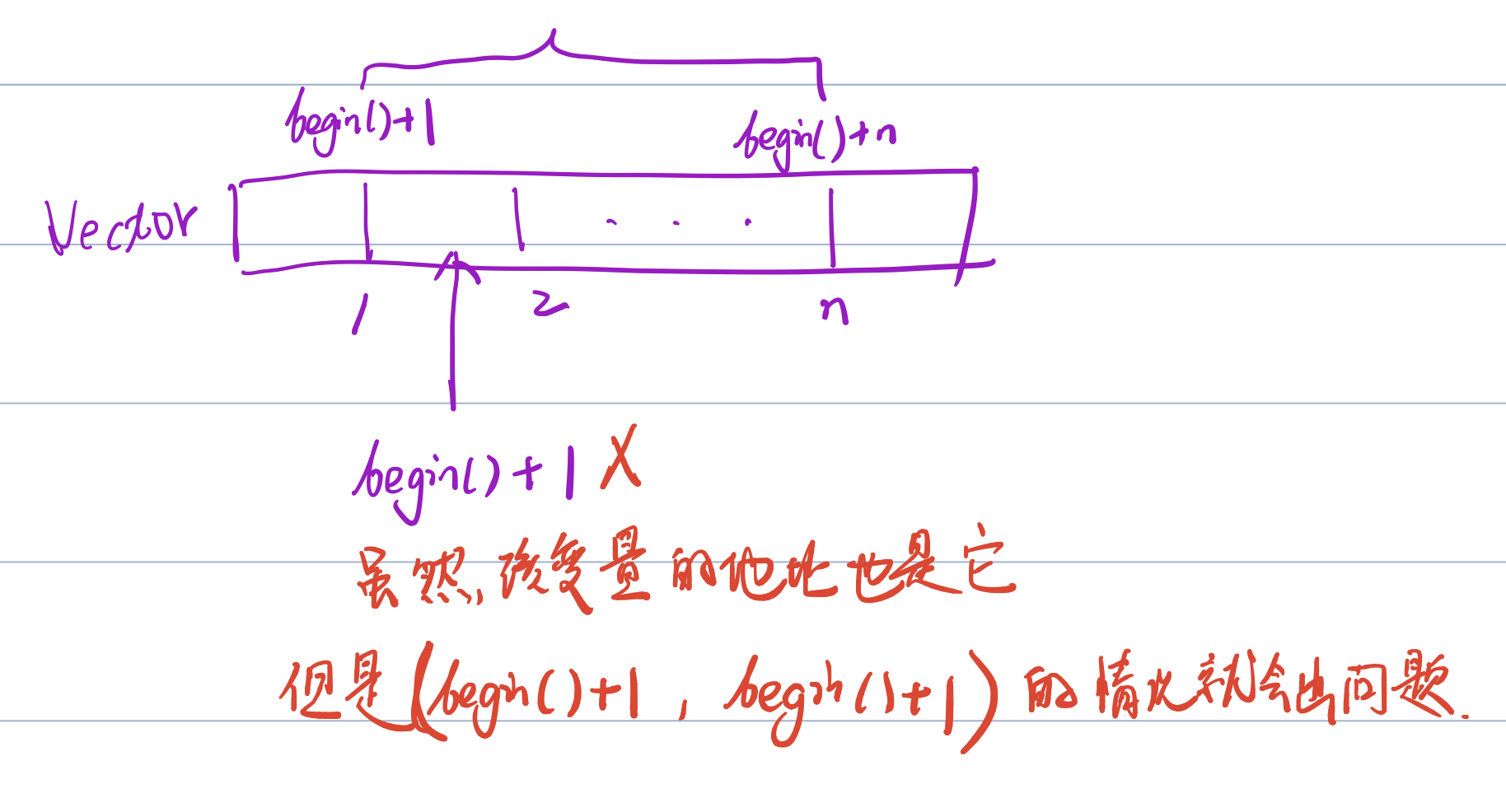
这是一个手动模拟的过程，每一步理解清楚，非常必要。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

class Solution {
public:
    int find(vector<int> vec, int target){
        for(int i=0; i<vec.size(); ++i){
            if(vec[i] == target) return i;
        }
        return -1;
    }

    TreeNode* reConstructBinaryTree(vector<int> pre,vector<int> vin) {
        if(pre.size()==0||vin.size()==0){
            return NULL;
        }
        TreeNode* p = (TreeNode*)malloc(sizeof(TreeNode));
        p->val = pre[0];
        int pos = find(vin, pre[0]);
        if(pre.begin() > pre.begin() + pos){
            p->left = NULL;
        }else{

            p->left = reConstructBinaryTree(vector<int>(pre.begin()+1, pre.begin()+pos+1),
                                            vector<int>(vin.begin(), vin.begin()+pos));
        }
        if(pre.begin() + pos + 1 > pre.end()){
            p->right = NULL;
        }else{
            p->right = reConstructBinaryTree(vector<int>(pre.begin()+pos+1, pre.end()),
                                             vector<int>(vin.begin()+pos+1, vin.end()));
        }
        return p;
    }


    void printTree(TreeNode* root){
        if(root==NULL) return;
        cout << root->val << ' ';
        printTree(root->left);
        printTree(root->right);
    }
};

5. 用两个栈实现队列

用两个栈来实现一个队列，完成队列的Push和Pop操作。 队列中的元素为int类型。

思路很简单，一个栈stack1用来push，另一个栈stack2用来pop。

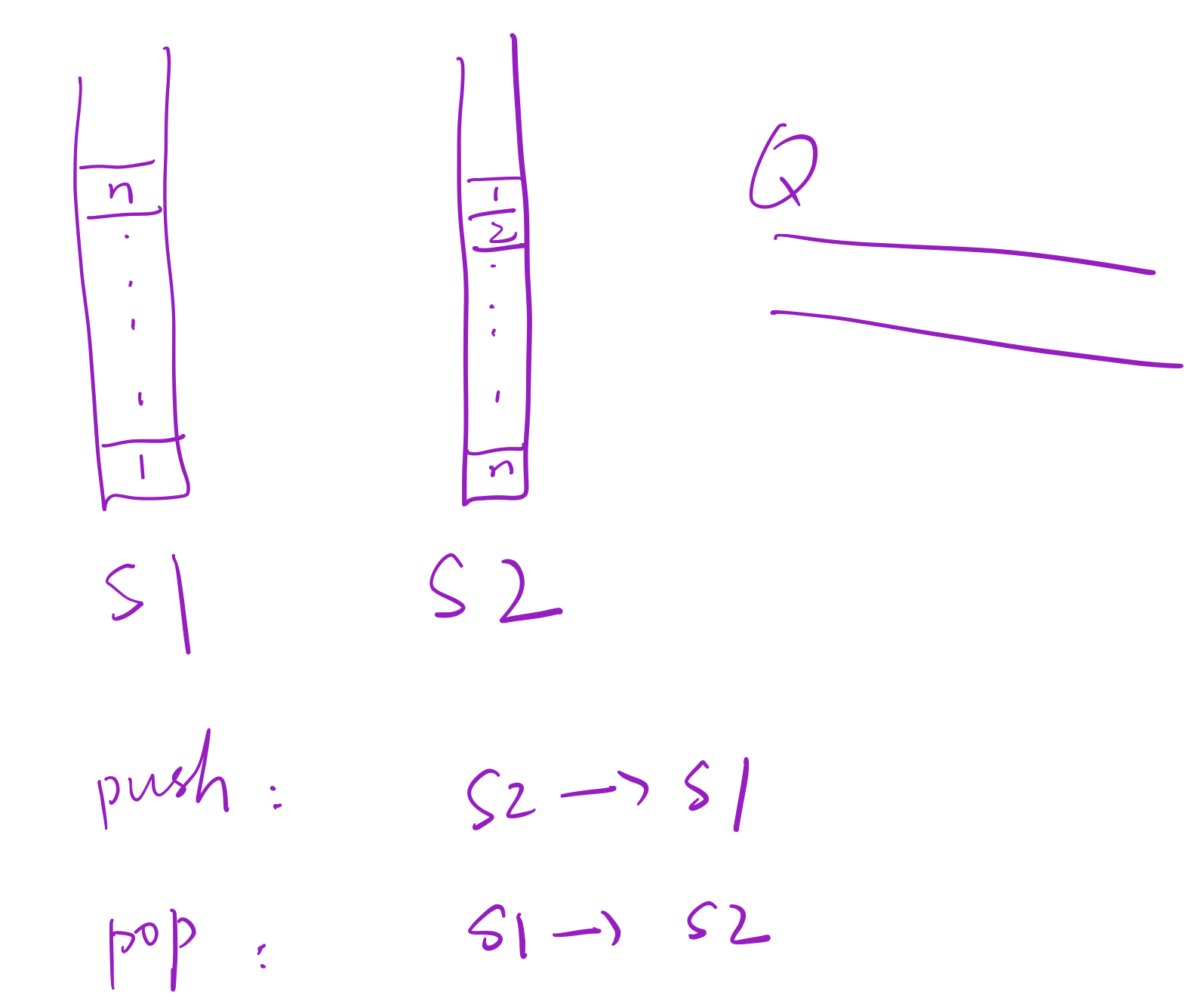
代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

class Solution
{
public:
    void push(int node) {
        while(!stack2.empty()){
            stack1.push(stack2.top());
            stack2.pop();
        }
        stack1.push(node);
    }

    int pop() {
        while(!stack1.empty()){
            stack2.push(stack1.top());
            stack1.pop();
        }
        int node = stack2.top();
        stack2.pop();
        return node;
    }

private:
    stack<int> stack1;
    stack<int> stack2;
};

6. 旋转数组的最小数字

把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。 输入一个非递减排序的数组的一个旋转，输出旋转数组的最小元素。 例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转，该数组的最小值为1。 NOTE：给出的所有元素都大于0，若数组大小为0，请返回0。

很简单的题目，找到最小的元素的位置，然后对相应元素进行搬移，输出搬移后的数组的第一个元素即可。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

class Solution {
public:
    int minNumberInRotateArray(vector<int> rotateArray) {
        if(rotateArray.size() == 0) return 0;
        int m = find_min(rotateArray);
        for(int i=0; i<m; ++i){
            rotateArray.push_back(rotateArray[i]);
        }
        rotateArray.erase(rotateArray.begin(), rotateArray.begin()+m);
        return rotateArray[0];

    }
    int find_min(vector<int> rotateArray){
        int m = 0;
        for(int i=0; i<rotateArray.size();++i){
            if(rotateArray[i]<rotateArray[m]){
                m = i;
            }
        }
        return m;
    }
    void print(vector<int> A){
        for(vector<int>::iterator it=A.begin();it!=A.end();++it){
            cout << *it << ' ';
        }
        cout << endl;
    }
};

7. 斐波那契数列

大家都知道斐波那契数列，现在要求输入一个整数n，请你输出斐波那契数列的第n项（从0开始，第0项为0）。 n<=39

斐波那契数列： F(1)=1，F(2)=1, F(n)=F(n - 1)+F(n - 2)（n ≥ 3，n ∈ N*）

斐波那契数列第一想法当然是递归，于是写递归算法， 内存超限。

于是使用迭代方法， AC。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

class Solution {
public:
    int Fibonacci(int n){
        if(n==0) return 0;
        int F, F_pre, F_pre_pre;
        F_pre = 1;
        F_pre_pre = 0;
        F = F_pre + F_pre_pre;
        for(int i=2; i<=n; ++i){
            F = F_pre + F_pre_pre;
            F_pre_pre = F_pre;
            F_pre = F;
        }
        return F;
    }

    // 递归， 超出内存限制
    int Fibonacci_1(int n) {
        if(n==1 || n == 2){
            return 1;
        }
        return Fibonacci(n-1) + Fibonacci(n-2);

    }
};

[8 9]. 跳台阶以及变态跳台阶

跳台阶

一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法（先后次序不同算不同的结果）。

一开始还是想着递归，然后时间超限， 放弃。

后来没什么思路， 百度得到结果， 原来思路和斐波那契数列是一样的。

另外，上楼梯比下楼梯想起来要容易一些。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

class Solution {
public:
    int jumpFloor(int number){
        if(number==2) return 2;
        if(number==1) return 1;
        int F, F_pre, F_pre_pre;
        F_pre = 2;
        F_pre_pre = 1;
        for(int i=3; i<=number; ++i){
            F = F_pre + F_pre_pre;
            F_pre_pre =F_pre;
            F_pre = F;
        }
        return F;
    }
    // 时间超限
    int jumpFloor_1(int number) {
        if(number==0) return 1;
        if(number<0) return 0;
        return jumpFloor(number-1) + jumpFloor(number-2);
    }
};

变态跳台阶

我们用f(n)来表示跳n级台阶的跳法数量

f(1)=1表示跳1级台阶的跳法数量;

f(2)=2表示跳2级台阶的跳法数量;

f(3)=f(2)+f(1)+1 我们可以递推出 f(n)=f(n-1)+f(n-2)+ *** +f(1)+1 ,

而f(n-1)=f(n-2)+ *** +f(1)+1。

将两式相减可以求出递推公式，也即是 f(n)-f(n-1)=f(n-1)，即f(n)=2*f(n-1);

代码：

1
2
3
4
5
6
7

class Solution {
public:
    int jumpFloorII(int number) {
        if(number == 1) return 1;
        return 2*jumpFloorII(number-1);
    }
};

10. 矩形覆盖

我们可以用2*1的小矩形横着或者竖着去覆盖更大的矩形。请问用n个2*1的小矩形无重叠地覆盖一个2*n的大矩形，总共有多少种方法？

比如n=3时，2*3的矩形块有3种覆盖方法：

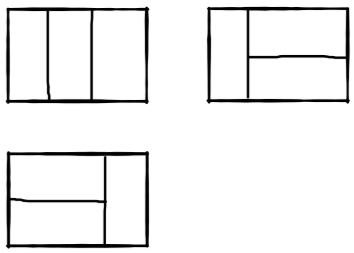
实际上，可以将这个问题转化为一个斐波那契数列的问题， 如图：

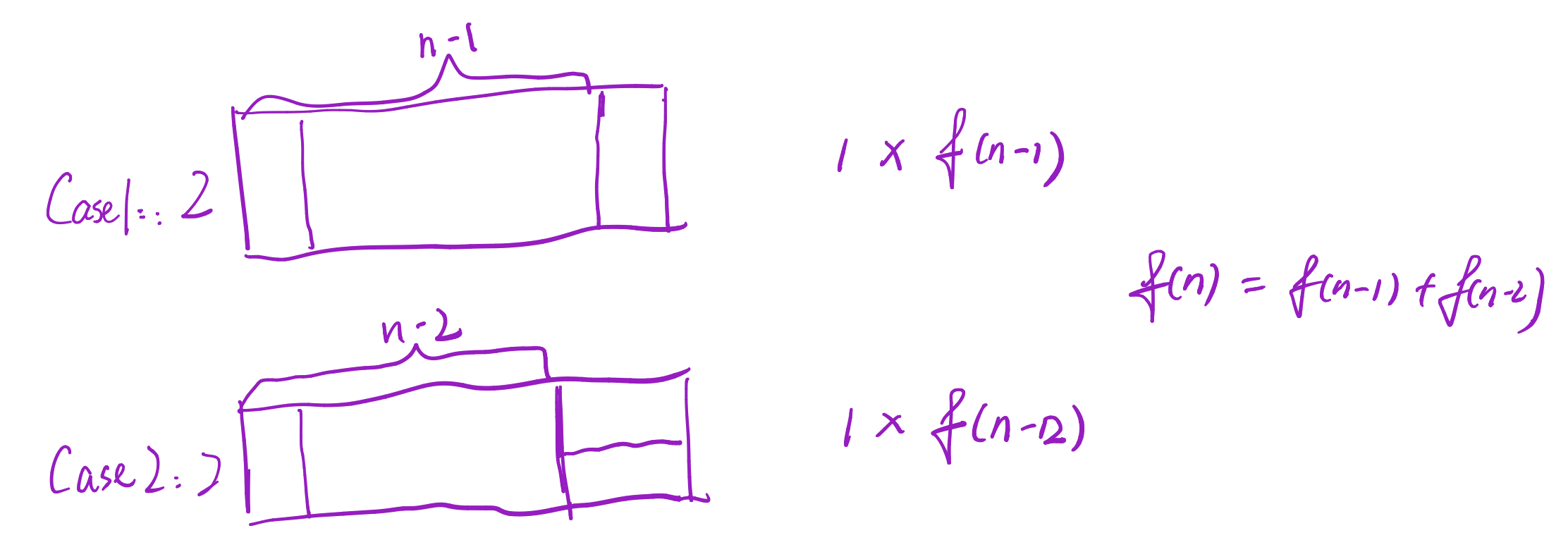
代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

class Solution {
public:
    // 斐波那契数列
    int rectCover(int number) {
        if(number==1) return 1;
        if(number==2) return 2;
        int F, F_pre, F_pre_pre;
        F_pre_pre = 1;
        F_pre = 2;
        F = 0;
        for(int i=3; i<=number; ++i){
            F = F_pre + F_pre_pre;
            F_pre_pre = F_pre;
            F_pre = F;
        }
        return F;
    }
};

11. 二进制中1的个数

解法一

第一种方法：令flag为无符号数1， 假设为32位， 那么flag即为0000 0000 0000 0001， 然后flag不断左移，如0000 0000 0000 0010, 0000 0000 0000 0100,…，直到溢出，此时flag = 0000 0000 0000 0000, 即0，也就是循环停止条件。每次左移与n进行按位与，若结果大于0，计数器count加一。

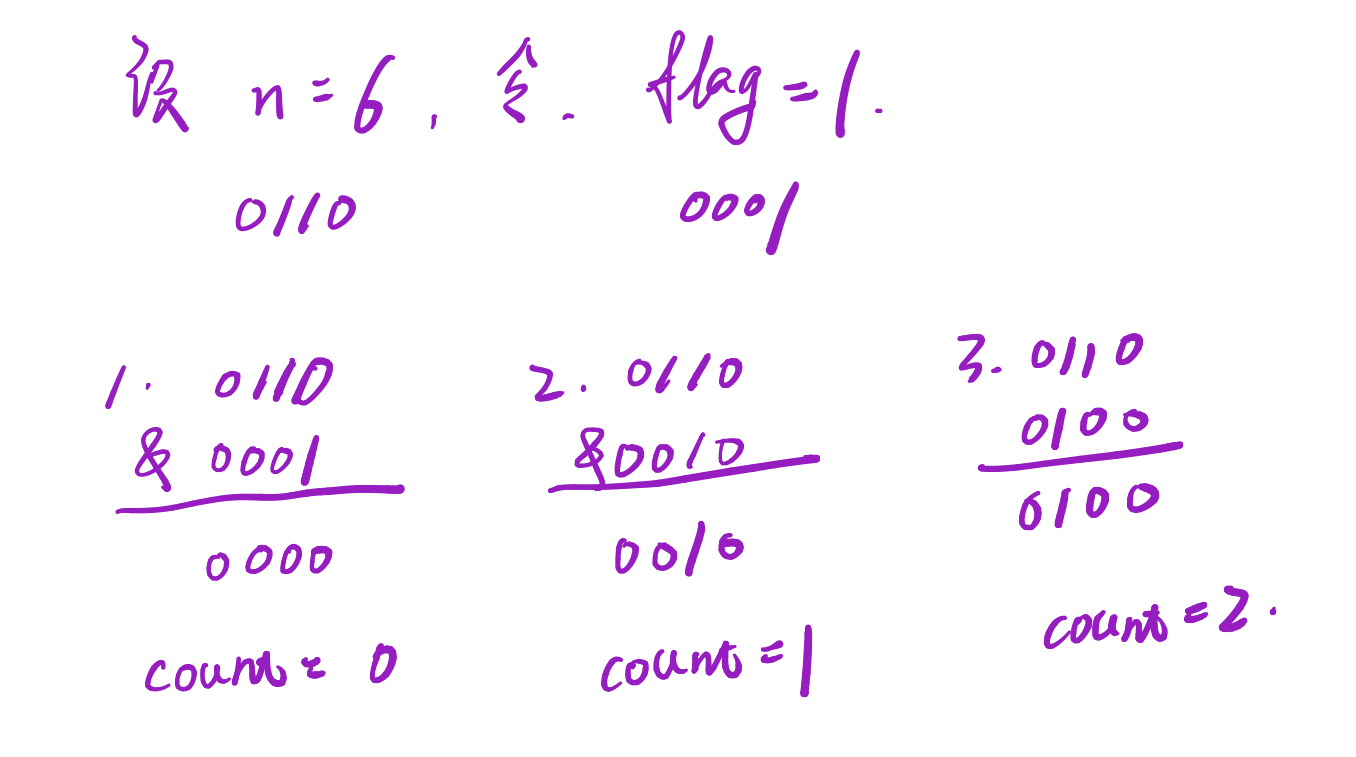
代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

class Solution {
public:
     int  NumberOf1(int n) {
         unsigned int flag = 1;
         int count = 0;
         while(flag >= 1){
            if((n&flag) > 0){
                ++count;
            }
            flag  = flag << 1;
         }
         return count;
     }
};

解法二

第二种方法：令无符号数a等于n， 然后a = a & (a - 1)循环， 这个等式的数学意义不好理解，但是记住它的功能就好， 它的功能是令a的二进制表示右边的1消失一个。循环结束条件是a=0， 每次循环计数器count加一。

代码：

1
2
3
4
5
6
7
8
9
10
11
12

class Solution {
public:
     int  NumberOf1(int n) {
         unsigned int a = n;
         int count = 0;
         while(a != 0){
            a = a & (a - 1);
            ++count;
         }
         return count;
     }
};

12. 数值的整数次方

很简单的一道题目。

主要考虑指数为正，为负， 为1的情况。

虽然人脑的计算的时候是$2 \times 2 \times 2$。但是计算机不能循环$base *= base$， 因为base是个变量，假设$base = 2$， 指数等于3，第一次运算结果base就等于4了，再运算就是4乘以4了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

class Solution {
public:
    double Power(double base, int exponent) {
        double out = base;
        if(exponent==0) return 1;
        if(exponent>0){
            for(int i=1; i<exponent; ++i){
                out *= base;
            }
        }
        if(exponent<0){
            base = 1.0 / base;
            out = base;
            for(int i=1; i<-exponent; ++i){
                out *= base;
            }
        }
        return out;

    }
};

13. 调整数组顺序使奇数位于偶数前面

思路一：刚看到这道题想到的就是这种方法， 创建一个和原数组相等大小的数组， 遍历两次原数组，第一次将奇数按序存入新数组，第二次将偶数按序存入新数组，最后新数组和原数组交换元素。

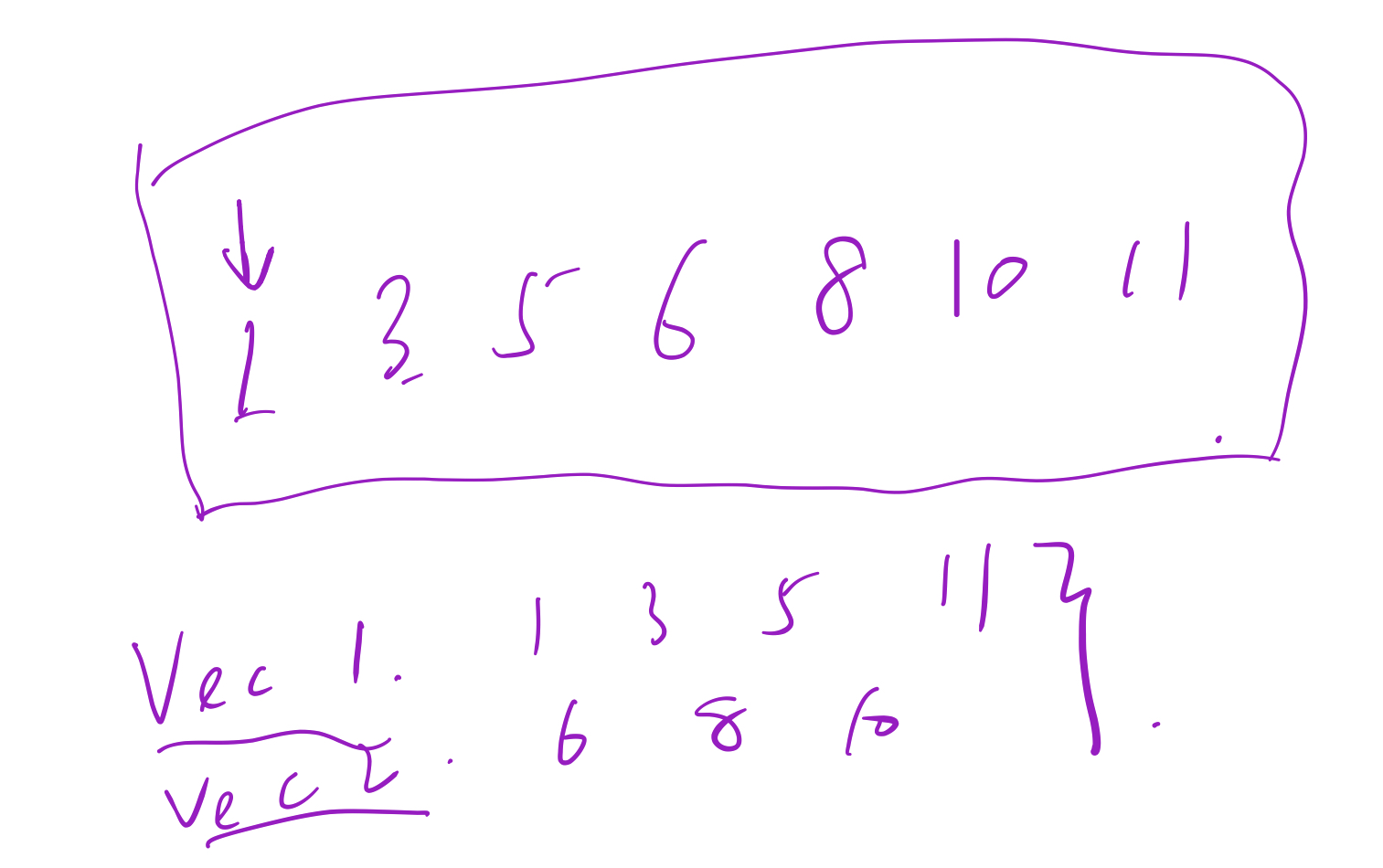
代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14

    void reOrderArray_1(vector<int> &array) {
        vector<int> tmp;
        for(vector<int>::iterator it=array.begin(); it!=array.end(); ++it){
            if(*it%2==1){
                tmp.push_back(*it);
            }
        }
        for(vector<int>::iterator it=array.begin(); it!=array.end(); ++it){
            if(*it%2==0){
                tmp.push_back(*it);
            }
        }
        array.swap(tmp);

思路2：

  • 先找到第一个偶数
  • 从第一个偶数后找到第一个奇数
  • 将第一个偶数和第一个奇数之间的元素（包含第一个偶数）往后移一位，这些元素是偶元素序列
  • 将第一个奇数填入到第一个偶数的位置
  • 循环2， 3， 4

也就是不断地在第一个偶元素的后面找奇元素，将偶序列后移，并将奇元素填到偶元素的位置

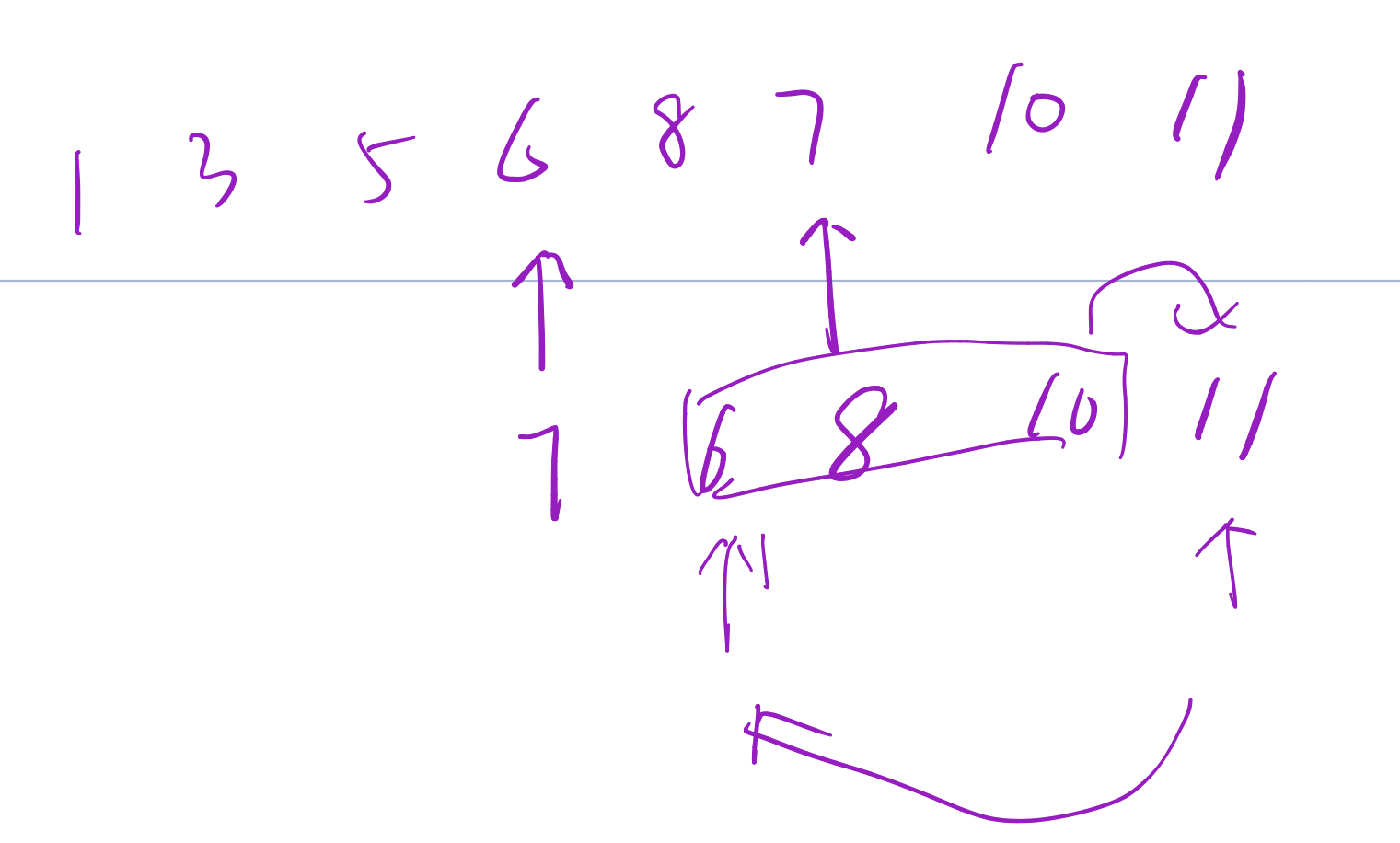
代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

    void reOrderArray(vector<int> &array) {
        if(array.size()==0) return;
        int i = 0, j, tmp;
        //找到第一个偶元素
        while(array[i]%2!=0) ++i;
        j = i+1;
        while(j<array.size()){
            //找到i之后的第一个奇元素
            while(array[j]%2==0) ++j;
            if(j>=array.size()) break;
            tmp = array[j];
            // i到j之间的偶元素后移一位
            for(int k=j; k>i; --k){
                array[k] = array[k-1];
            }
            array[i] = tmp;
            ++i;
            j = i+1;
        }

    }

14. 链表中倒数第k个结点

这个题想起来很容易，但是情况比较多，需要分别讨论。

  • 当k小于等于0时，返回NULL
  • 当k大于链表长度时，返回NULL
  • 当k在链表中时，遍历链表得到长度，再一个循环即可得到目标元素

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

class Solution {
public:
    ListNode* FindKthToTail(ListNode* pListHead, unsigned int k) {
        if(pListHead==NULL) return NULL;
        if(k<=0) return NULL;
        ListNode* p = pListHead;
        int length = 0;
        while(p!=NULL){
            length++;
            p = p->next;
        }
        if(k>length) return NULL;
        p = pListHead;
        for(int i=0; i<length-k; ++i){
            p = p->next;
        }
        return p;
    }
    void CreateLinkList(ListNode* &L, int n){
        ListNode* p = (ListNode*)malloc(sizeof(ListNode));
        p->val = 1;
        p->next = NULL;
        L = p;
        for(int i=n; i>1; --i){
            p = (ListNode*)malloc(sizeof(ListNode));
            p->next = L->next;
            p->val = i;
            L->next = p;
        }
    }
    void printLinkList(ListNode* L){
        ListNode* p = L;
        while(p!=NULL){
            cout << p->val << ' ';
            p = p->next;
        }
        cout << endl;
    }
};

15. 反转链表

题目很简单，用头插法即可，用指针p定位要插入的元素，用指针r定位原链表的下一元素位置，要注意p和r的位置关系，以及循环停止条件。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

class Solution {
public:
    // 头插法
    ListNode* ReverseList(ListNode* pHead){
        if(pHead==NULL) return NULL;
        if(pHead->next==NULL) return pHead;
        ListNode *p = pHead, *r = pHead->next;
        ListNode* H = (ListNode*)malloc(sizeof(ListNode));
        H->next = NULL;
        while(r!=NULL){
            r = p->next;
            p->next = H->next;
            H->next = p;
            p = r;

        }
        p = H->next;
        delete H;
        return p;
    }
    void CreateLinkList(ListNode* &L, int n){
        ListNode* p = (ListNode*)malloc(sizeof(ListNode));
        p->val = 1;
        p->next = NULL;
        L = p;
        for(int i=n; i>1; --i){
            p = (ListNode*)malloc(sizeof(ListNode));
            p->next = L->next;
            p->val = i;
            L->next = p;
        }
    }
    void printLinkList(ListNode* L){
        ListNode* p = L;
        while(p!=NULL){
            cout << p->val << ' ';
            p = p->next;
        }
        cout << endl;
    }
};

16. 合并两个排序的链表

这个题目在考研初试时练的很多，很简单的题目。

指针p1用于遍历链表1， 指针p2用于遍历链表2， 比较两个指针指向元素的大小，用另一个指针p将它们串起来。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

class Solution {
public:
    ListNode* Merge(ListNode* pHead1, ListNode* pHead2)
    {
        ListNode *p1 = pHead1, *p2 = pHead2;
        ListNode *H = (ListNode*)malloc(sizeof(ListNode));
        H->next = NULL;
        ListNode *p = H;
        while(p1!=NULL && p2!=NULL){
            if(p1->val>p2->val){
                p->next = p2;
                p = p2;
                p2 = p2->next;
            }else{
                p->next = p1;
                p = p1;
                p1 = p1->next;
            }
        }
        if(p1!=NULL) p->next = p1;
        if(p2!=NULL) p->next = p2;
        p = H->next;
        delete H;
        return p;
    }
    void CreateLinkList(ListNode* &L, int n){
        ListNode* p = (ListNode*)malloc(sizeof(ListNode));
        p->val = 1;
        p->next = NULL;
        L = p;
        for(int i=n; i>1; --i){
            p = (ListNode*)malloc(sizeof(ListNode));
            p->next = L->next;
            p->val = i;
            L->next = p;
        }
        if(n==0) L = NULL;
    }
    void printLinkList(ListNode* L){
        ListNode* p = L;
        while(p!=NULL){
            cout << p->val << ' ';
            p = p->next;
        }
        cout << endl;
    }
};

17. 树的子结构

enter description here

递归查找子结构

  • 当树2为空或树2不为空且树1为空时，若是， 返回0
  • 判断树1从根节点开始有没有树2的子结构，若是， 返回1
  • 递归判断树1的左子树从根节点开始有没有树2的子结构，若是， 返回1
  • 递归判断树1的右子树从根节点开始有没有树2的子结构， 若是，返回1
  • 否则，返回0

关键是写一个从根节点开始判断一棵树是否是另一棵树的一部分的函数， 注意这个并不是判断两个树是否相似，也就是说当树2到了树底的时候，树1未必到了树底。因此，我们以树2的结构依次判断树1中是否有对应的元素即可。

判断的条件为：

  • 当树2为空时，返回1
  • 当树2不为空，树1为空时，返回0
  • 当树2不为空，树1也不为空，树1与树2的值相等时，返回1
  • 当树2不为空，树1也不为空，树1与树2的值不相等时，返回0
  • 然后递归分别判断左子树和右子树

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

class Solution {
public:
    bool HasSubtree(TreeNode* pRoot1, TreeNode* pRoot2)
    {
        if(pRoot2==NULL || (pRoot1==NULL&&pRoot2!=NULL)) return 0;
        if(Tree_if_same(pRoot1, pRoot2)==1) return 1;
        if(HasSubtree(pRoot1->left, pRoot2)) return 1;
        if(HasSubtree(pRoot1->right, pRoot2)) return 1;
        return 0;
    }
    bool Tree_if_same(TreeNode* pRoot1, TreeNode* pRoot2){
        if(pRoot2==NULL) return 1;
        if((pRoot1==NULL&&pRoot2!=NULL)) return 0;
        if(pRoot1->val!=pRoot2->val) return 0;
        else{
            return Tree_if_same(pRoot1->left, pRoot2->left) & Tree_if_same(pRoot1->right, pRoot2->right);
        }

    }
    void Tree_Structor(TreeNode* &T, int n){
        if(n<=0){T = NULL; return;}
        T = (TreeNode*)malloc(sizeof(TreeNode));
        T->val = n;
        Tree_Structor(T->left, n-1);
        Tree_Structor(T->right, n-2);
    }
    void print_Tree(TreeNode* T){
        if(T==NULL) return;
        cout << T->val << ' ';
        print_Tree(T->left);
        print_Tree(T->right);
    }
};

18. 二叉树的镜像

![](https://raw.githubusercontent.com/ShawnDong98/ShawnDong98.github.io/master/小书匠/1583493123539.png

将根节点的左右子树交换。

递归分别将子树的左右子树交换即可。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

class Solution {
public:
    void Mirror(TreeNode *pRoot) {
        if(pRoot==NULL) return;
        TreeNode* p = (TreeNode*)malloc(sizeof(TreeNode));
        p->left = pRoot->left;
        p->right = pRoot->right;
        pRoot->left = p->right;
        pRoot->right = p->left;
        delete p;
        Mirror(pRoot->left);
        Mirror(pRoot->right);
    }
    void Tree_Structor(TreeNode* &T, int n){
        if(n<=0){T = NULL; return;}
        T = (TreeNode*)malloc(sizeof(TreeNode));
        T->val = n;
        Tree_Structor(T->left, n-1);
        Tree_Structor(T->right, n-2);
    }
    void print_Tree(TreeNode* T){
        if(T==NULL) return;
        cout << T->val << ' ';
        print_Tree(T->left);
        print_Tree(T->right);
    }
};

Reference

  1. 剑指offer(1)二维数组中的查找
  2. 静态数组不能扩容（realloc），动态的才可以（如何创建动态数组）
  3. [剑指Offer 跳台阶](https://blog.csdn.net/mengmengdastyle/article/details/80304755?depth_1-utm_source=distribute.pc_relevant.none-task&utm_source=distribute.pc_relevant.none-task)
  4. 变态跳台阶（剑指offer第九题）
  5. 剑指offer——矩形覆盖问题
  6. 牛客网_剑指offer_二进制中1的个数
  7. 【剑指offer】面试题21：调整数组顺序使奇数位于偶数前面
  8. 《剑指offer》 链表中倒数第k个节点
CATALOG
    FEATURED TAGS
    mark 深度学习 机器学习 HSI Detection d2l Geek GAN 课业笔记 Diffusion CVPR 2023 Research & Writing low-level CV CVPR 2022 ICCV 2023 Scene Graph CV ECCV 2022 NLP MMML Backbone Arxiv 2022 NIPS 2022 CVPR 2020 NIPS 2021 Segmentation GNN & GCN 计算方法 CVPR 2018 CVPR 2021 ECCV 2020 ICCV 2019 强化学习 FastAI arXiv 2023 凸优化 操作系统 数据结构 矩阵论 离散数学 计算机网络 Arxiv 2021 CVPR 2019 ICCV 2021 OpenCV VAE Arxiv 2020 Arxiv 2023 CVPR 2017 ICCV 2017 ICLR 2021 Life TPAMI 2023 学会理财 嵌入式 生活 算法 计算智能 CVPR 2016 CVPRW 2022 CVPRW 2023 Docker ICLR 2022 MMLab Python Research & Competition TGRS 2023 TIP 2013 TIP 2021 TMM 2023 TPAMI 2017 TPAMI 2019 TPAMI 2022 WACV 2024
    FRIENDS