集合

集合的势

集合的势表示集合中有多少元素，记作$\mid S \mid$。

集合的表示：

列元素法： $A = \{a, b, c, d\}$
谓词表示法：$B = \{x \mid P(x)\}$

例子：

$A = \{a, \{b, c\}, d, \{\{d\}\}$ $\{b, c\} \in A$
注意这是属于，不是包含，如果写成包含就错了 $b \notin A$
$\{\{d\}\} \in A$
$\{d\} \notin A$
$d \in A$

外延公理

两个集合A和B相等，即A＝B，当且仅当它们有相同的成员。用逻辑符号表达：

\[A = b \Leftrightarrow \forall x (x \in A \leftrightarrow x \in B) \\ \Leftrightarrow \forall x(x \in A \rightarrow x \in B) \land \forall x(x \in B \rightarrow x \in A)\]

例子：

证明以下公式：

\[A - B = A \cap \thicksim B\]

思考：怎么证？

幂集

设A是一个集合，A的所有子集的集合称为A的幂集，记为ρ(A)。即

\[\rho(A) = \{B \mid B \subseteq A \}\]

如果A是有限集，则ρ(A)的元素个数也是有限的。即如果$\mid A \mid=n$，则 $\mid ρ(A) \mid =2^n$。

例子：

（1）$P(\phi)$

\[A = \phi, \quad P(A) = {\phi}\]

（2）$P(\{\phi\})$

\[A = \{\phi\}, \quad P(A) = \{\phi, \{\phi\}\}\]

（3）$P(\{1, \{2, 3\}\})$

\[A = \{a, b\}, \quad a = \{1\}, \quad b = \{2, 3\} \\ P(A) = \{\phi, \{a\}, \{b\}, \{a, b\}\}, \quad P(A) = \{\phi, \{1\}, \{2, 3\}, \{1, \{2, 3\}\}\}\]

集合上的运算

交($\cap$)、并($\cup$)、差($-$)、补($\bar A$)

交换律，结合律，分配率

容易忘的公式：

\[A - B \subseteq A\] \[A \subseteq B \Rightarrow \bar B \subseteq \bar A\]

环和（对称差）

\[A \oplus = (A-B) \cup (B - A) \\ = \{x \mid x \in A \land x \notin B \lor x \in B \land x \notin A\}\]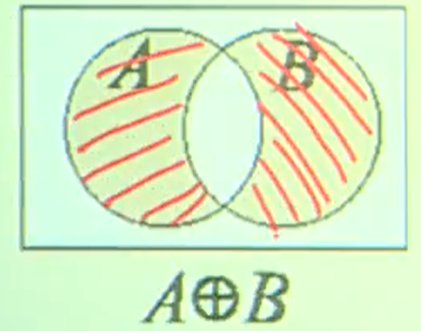

性质：

$A \oplus B = (A \cup B) \cap (\bar A \cup \bar B) = (A \cup B) - (A \cap B)$
$A \oplus B = \bar A \oplus \bar B \quad A \oplus B = B \oplus A \quad A \oplus A = \Phi$
$(A \oplus B)\oplus C = A \oplus (B \oplus C)$
$C \cap (A \oplus B) = (C \cap A)\oplus (C \cap B)$ 只有交对对称差有分配律
$A \cup (B \oplus C) \neq (A \cup B) \oplus (A \cup C)$
$A \oplus (B \cap C) \neq (A \oplus B) \cap (A \oplus C)$

	$\cup$	$\cap$	$\oplus$
交换	$A \cup B = B \cup A$	$A \cap B = B \cap A$	$A \oplus B = B \oplus A$
结合	$(A \cup B) \cup C = A \cup (B \cup C)$	$(A \cap B) \cap C = A \cap (B \cap C)$	$(A \oplus B) \oplus C = A \oplus (B \oplus C)$
幂等	$A \cup A = A$

	$\cup 与 \cap$	$\cap 与 \oplus$
分配	$A \cup (B \cap C) = (A \cup B) \cap (A \cup C) \ A \cap (B \cup C) = (A \cap B) \cup (A \cap C)$	$A \cap (B \oplus C) = (A \cap B) \oplus (A \cap C)$
吸收	$A \cup (A \cap B) = A \ A \cap (A \cup B) = A$

	$-$	$\thicksim$
DM律	$A - (B \cup C) = (A - B) \cap (A - C) \ A - (B \cap C) = (A - B) \cup (A - C)$	$\thicksim (B \cup C) = \thicksim B \cap \thicksim C$
双重否定		$\thicksim \thicksim A = A$

	$\phi$	$E$
补元律	$A \cap \thicksim A = \phi$	$A \cup \thicksim A = E$
零律	$A \cap \phi = \phi$	$A \cup E = E$
同一律	$A \cup \phi = A$	$A \cap E = A$
否定	$\thicksim \phi = E$	$\thicksim E = \phi$

一些重要结果：

$\phi \subseteq A - B \subseteq A$
$A \subseteq B \Leftrightarrow A - B = \phi \Leftrightarrow A \cup B = B \Leftrightarrow A \cap B = A \quad（包含的等价条件）$
$A \cap B = \phi \Leftrightarrow A - B = A$
$A - B = A \cap \thicksim B$
$A - B = A - (A \cap B)$

例子：

证明$X = Y$

互为子集法
集合运算法
反证法(通常在证明某集合等于空集时使用)

环积

\[A \otimes B = \overline{A \oplus B} = \overline {(A \cap \bar B) \cup (B \cap \bar A)} \\ = (A \cup \bar B) \cap (B \cup \bar A) = (A \cap B) \cup (\bar A \cap \bar B) \\ = \{x \mid x \in A \land x \in B \lor x \notin A \land x \notin B\}\]

性质：

$A \otimes B = \bar A \otimes \bar B \quad A \otimes B = B \otimes A \quad A \otimes A = U$
$(A \otimes B) \otimes C = A \otimes (B \otimes C)$
$A \cup (B \otimes C) = (A \cup B) \otimes (A \cup C)$

思考：这里一脸懵逼

容斥原理

设 A, B是有限集合，其元素个数为$\mid A \mid$, $\mid B \mid$, 则:

\[\mid A \cup B| = \mid A \mid + \mid B \mid - \mid A \cap B \mid\]

推广：设A，B，C是有限集合，则：

\[\mid A \cup B \cup C \mid = \mid A \mid + \mid B \mid + \mid C \mid - \mid A \cap B \mid - \mid A \cap C \mid - \mid B \cap C \mid + \mid A \cap B \cap C \mid\]

例子：

一个班级有50个学生，有26人在第一次考试中得到A，21人在第二次考试中得到A，假如有17人两次考试都没有得到A，问有多少学生在两次考试中都得到A。

解：

设第一次考试得到A的学生集合为A，第二次考试得到A的学生集合为B，则：

\[\mid A \cup B \mid = 50 - 17 = 33\]

而：

\[\mid A \cup B \mid = \mid A \mid + \mid B \mid - \mid A \cap B \mid\]

所以：

\[\mid A \cap B \mid = \mid A \mid + \mid B \mid - \mid A \cup B \mid = 26 + 21 -33 = 14\]

即两次考试都得A的学生有14人。

笛卡尔乘积

两个元素a1,a2组成的序列记作<a1,a2>, 称为二重组或序偶。a1,a2分别称为序偶<a1,a2>的第一分量和第二分量。

两个序偶<a,b>和<c,d>相等当且仅当a=c且b=d。

口语描述：序偶就是一个有序对，比如在平面直角坐标系中， (x, y)是一个有序对，它不等于(y, x)

设a1,a2,…,an是n个元素，定义<a1,a2,…,an>=<<a1,a2,…,an-1>,an>为n重组。（n>2）

Note：

序偶中元素的次序是重要的，与集合不同
n重组是一个序偶，第一个分量是一个n-1重组
两个n重组<a1,a2,…,an>和<b1,b2,…,bn>相等当且仅当ai=bi，1≤i≤n。

集合A和B的叉积（直积、笛卡儿乘积）记为A×B，是序偶集合

\[\{<a, b> \mid a \in A \land b \in B\}\]

性质：

$\mid A_1 \times A_2 \times … \times A_n \mid = \mid A_1 \mid \mid A_2 \mid … \mid A_n \mid$
不可交换，不可结合
$A \times (B \cup C) = (A \times B) \cup (A \times C)$
$A \times (B \cap C) = (A \times B) \cap (A \times C)$
$(A \cup B) \times C = (A \times C) \cup (B \times C)$
$(A \cap B) \times C = (A \times C) \cap (B \times C)$

\[A \times (B \cup C) = (A \times B) \cup (A \times C)\]

证明：

\[<x, y> \in A \times (B \cup C) \Leftrightarrow x \in A \land y \in (B \cup C) \\ \Leftrightarrow x \in A \land (y \in B \lor y \in C) \\ \Leftrightarrow x \in A \land y \in B \lor x \in A \land y \in C \\ \Leftrightarrow <x, y> \in A \times B \lor <x, y> \in A \times C \\ \Leftrightarrow <x, y> \in (A \times B) \cup (A \times C)\]

例子：

\[A = \{\phi\}, P(A) \times A = \{<\phi, \phi>. <\{\phi\}, \phi>\}\]

解：

\[a = \phi \\ A = \{a\} \quad P(A) = \{\phi, \{a\}\} \\ P(A) \times A = \{<\phi, a>, <\{a\}, a>\} = \{<\phi, \phi>, <\{\phi\}, \phi>\}\]

关系

关系的基本概念

A×B的子集称为A到B的一个二元关系。

A1×A2×…×An的子集称为A1×A2×…×An上的一个n元关系。

An＝A×A×…×A(n个A)的子集称为A上的n元关系。特别的， A2＝A×A的子集称为A上的二元关系。

关系通常用R表示，二元关系R中任一序偶<x,y>可记作 <x,y>∈R或xRy。

二元关系

令R为集合X到集合Y的二元关系，由<x,y>∈R的所有x组成的集合D(R)称为R的定义域，即：

\[D(R) = \{x \mid \exists y (<x, y> \in R)\}\]

由<x,y>∈R的所有y组成的集合R(R)称为R的值域，即:

\[R(R) = \{y \mid \exists x (<x, y> \in R)\}\]

X叫做关系R的前域，Y叫做关系R的陪域。

设Ix是X上的二元关系，且满足$Ix=\{<x,x> \mid x∈X\}$，则称Ix(或 Ex)是X上的相等关系。

设R是A1×A2×…×An的子集，如果R＝Φ，则称R为空关系。如果R＝ A1×A2×…×An，则称R为全域关系。

二元关系的表示

关系的矩阵表示：

设给定两个有限集合X={x1,x2,…xm}，Y={y1,y2,…,yn}，R为从X到Y的一个二元关系。则对应于关系R有一个关系矩阵$M_R=[r_{ij}]_{m×n}$。其中，

\[r_{ij} = \begin{cases} 1 & <x_i, y_j> \in R \\ 0 & <x_i, y_j> \notin R \end{cases} \quad \text{i = 1, 2, ..., m, j=1, 2, ..., n}\]

关系的图形表示：

设给定两个有限集合X={x1,x2,…xm}，Y={y1,y2,…,yn}，R为从X到Y的一个二元关系。首先在平面上作出m个结点分别记为x1,x2,…,xm，然后另外作出n个结点分别记为y1,y2,…,yn，如果xiRyj，则可自结点xi至结点yj处作一有向弧，其箭头指向yj。这种方法联结起来的图就称为R的关系图。

如果X和Y是同一个集合，可以只画出一个集合的结点

二元关系的性质

自反

设R是集合X上的二元关系，如果对于X中的每个x，有xRx，则称二元关系R是自反的。

\[R在X上自反 \Leftrightarrow (\forall x)(x \in X \rightarrow xRx)\]

设R是集合X上的二元关系，如果对于X中的每个x，有$x \not Rx$，则称二元关系R是反自反的。

\[R在X上反自反 \Leftrightarrow (\forall x)(x \in X \rightarrow x \not R x)\]

关系R是反自反的，当且仅当其关系图中每个结点都没有自回路，其关系矩阵的主对角线上元素都为0。

有些关系既不是自反的，又不是反自反的。如：集合A={1,2,3}，R={<1,1>,<1,2>, <2,3>,<3,2>,<3,3>}。

例子：

自反关系：A上的全域关系$E_A$，恒等关系$I_A$，小于等于关系$L_A$，整除关系$D_A$

反自反关系：实数集上的小于关系，幂集上的真包含关系

对称

设R是集合X上的二元关系，如果对于X中的每个x，y，每当xRy，就有yRx，则称二元关系R是对称的。

\[R在X上对称 \Leftrightarrow (\forall x)(\forall y)(x \in X \land y \in Y \in X \land xRy \rightarrow yRx)\]

关系R是对称的，当且仅当其关系图中任意两个结点间若有定向弧，必是成对出现的，其关系矩阵关于主对角线对称。

设R是集合X上的二元关系，如果对于X中的每个x，y，每当xRy和yRx，必有x=y，则称二元关系R是反对称的。

\[R在X上反对称 \Leftrightarrow (\forall x)(\forall y)(x \in X \land y \in X \land xRy \land yRx \rightarrow x = y)\] \[R在X上反对称 \Leftrightarrow (\forall x)(\forall y)(x \in X \land y \in X \land x \neq y \land xRy \rightarrow y \not R x)\]

关系R是反对称的，当且仅当其关系图中任意两个结点间的定向弧不能成对出现，其关系矩阵中关于主对角线对称的元素不能同时为1。

有些关系既不是对称的，又不是反对称的。如：集合A={1,2,3}，R={<2,1>,<1,2>, <2,3>}。

有些关系既是对称的，也是反对称的。如：集合A={1,2,3}，R={<1,1>,<2,2>, <3,3>}。

例子：

对称关系：A上的全域关系$E_A$，恒等关系$I_A$和空关系$\emptyset$

反对称关系：恒等关系$I_A$，空关系是A上的反对称关系

【判断题】设A = {1， 2， 3}， $R_1, R_2, R_3和R_4$都是A上的关系，其中

\[R_1 = \{<1, 1> , <2, 2>\}\]

对称的：$对于xRy, 有yRx$

反对称的：$对于xRy和yRx，有x=y$

\[R_2 = \{<1, 1>, <1, 2>, <2, 1>\}\]

对称的：$对于xRy, 有yRx$

不是反对称的：$对于xRy和yRx，x \neq y$

\[R_3 = \{<1, 2>, <1, 3>\}\]

不是对称的：$对于xRy, 没有yRx$

反对称的：$因为没有xRy和yRx的情况，所以是反对称的$

\[R_4 = \{<1, 2>, <2, 1>, <1, 3>\}\]

不是对称的：$不是所有的x对于xRy,有yRx$

不是反对称的：$对于xRy和yRx，有x \neq y$

传递

设R是集合X上的二元关系，如果对于X中的每个x，y，z，每当xRy，yRz，就有xRz，则称二元关系R是传递的。

\[R在X上传递 \Leftrightarrow (\forall x)(\forall y)(\forall z)(x \in X \land y \in X \land z \in X \land xRy \land yRz \rightarrow xRz)\]

例子：

整数集合I上，关系≤ 是：自反的，反对称的，传递的，但不是反自反的和对称的；
整数集合I上，关系<是：反自反的，反对称的，传递的，但不是自反的和对称的。
任何集合上的相等关系是：自反的，对称的，反对称的，传递的，但不是反自反的。
非空集合上的空关系是：反自反的，对称的，反对称的，传递的，但不是自反的。
基数大于1的集合上的全域关系是：自反的，对称的，传递的，但不是反自反的和反对称的。

A上的全域关系$E_A$，恒等关系$I_A$和空关系$\emptyset$ 小于等于关系，小于关系，整除关系，包含关系，真包含关系

关系矩阵的布尔运算

并

交

布尔积

逆关系

设R为X到Y的二元关系，如果将R中每一序偶的元素顺序互换，所得到的集合称为R的逆关系。记作$\tilde R$，即：

\[\tilde R = \{<y, x> \mid <x, y> \in R\}\]

性质

$(\tilde {\tilde R}) = R$
$(R_1 \tilde \cup R_2) = \tilde R_1 \cup \tilde R_2)$
$(R_1 \tilde \cap R_2) = \tilde R_1 \cap \tilde R_2$
$(A \tilde \times B) = B \times A$
$(\tilde {\bar R)} = \bar {\tilde R} \quad 其中 \bar R = A \times B - R$
$(R_1 \simeq R_2) = \tilde R_1 - \tilde R_2$
$R_1 \subseteq R_2 \Rightarrow \tilde R_1 \subseteq \tilde R_2$

设R是X上的二元关系，则：

R是对称的，当且仅当$R = \tilde R$
R是反对称的，当且仅当$R \cap \tilde R$是Ix的子集

关系$\tilde R$的图形，是关系R图形中将其弧的箭头方向反置。

关系$\tilde R$的关系矩阵$M_{\tilde R}$是R的关系矩阵$M_R$的转置矩阵$M_R^T$

定理

设R和S时集合A到B的二元关系。则：

若$R \subseteq S$，则$R^{-1} \subseteq S^{-1}$
若$R \subseteq S$，则$S^c \subseteq R^c$
$(R \cap S)^{-1} = R^{-1} \cap S^{-1}$
$(R \cup S)^{-1} = R^{-1} \cup S^{-1}$
$(R \cap S)^c = R^c \cup S^c$
$(R \cup S)^c = R^c \cap S^c$

合成关系(复合关系)

类似于传递

设R为X到Y的关系，S为从Y到Z的关系，则RS称为R到S的合成关系，表示为

\[RS = \{<x, z> \mid x \in X \land z \in Z \land \exists y(y \in Y \land <x, y> \in R \land <y, z> \in S)\}\]

从R和S，求RS称为关系的合成运算。

设R为A上的关系，n为自然数，则R的n次幂定义为：

\[R^0 = \{ <x, x> \mid x \in A \} = I_A\]
$R^{n+1} = R^n R$

$R^2$实际上所描述的含义是R的关系图中距离为2的节点。

性质

不可交换
（可以结合）：设R1，R2和R3分别是从A和B， B到C和C到D的关系，那么（R1R2）R3 = R1（R2R3）。
设R是从X到Y的二元关系， Ix和Iy分别是X和Y上的相等关系，则IxR = RIy = R。
设R1是从A到B的关系，R2和R3是从B到C的关系，R4是从C到D的关系，那么：（a） $R1(R2 \cup R3) = R1R2 \cup R1R3$
（b） $R1(R2 \cap R3) \subseteq R1R2 \cap R1R3$
（c） $(R2 \cup R3)R4) = R2R4 \cup R3R4$
（c） $(R2 \cup R3)R4) \subseteq R2R4 \cup R3R4$

关系的幂： $RR = R^2, RRR = R^3, …, R^{n+1} = R^nR$

定义 $R^0 = Ix$
$R^mR^n = R^{m+n}, (R^m)^n = R^{mn}$

设$\mid A \mid = n$， R是集合A上的一个关系，那么存在i和j使$R^i = R^j$，且$0 \leq i < j \leq 2^{n^2}$。

设R是集合A上的一个二元关系，若存在i和j使$R^i = R^j$，且i<j，记d = j - i, 则：

对所有$k \geq 0, R^{i+k} = R^{j+k}$
对所有$k, m \geq 0, R^{i+md+k} = R^{i+k}$
记$S = \{R^0, R^1, R^2, ..., R^{j-1}\}$

那么R的每一次幂是S的元素，即对$n \in N, R^n \in S$

定理

【定理】设F、G、H是任意的关系，则：

$(FG)H = F(GH)$
$(FG)^{-1} = G^{-1}F^{-1}$

【定理】设集合A、B、C均为有限集， $A=\{a_1, a_2, ..., a_m\}$, $B = \{b_1, b_2, ..., b_n\}$, $C = \{c_1, c_2, ..., c_p\}$， R是A到B的二元关系， S是B到C的二元关系，则：

\[M_{RS} = M_R \odot M_S\]

【定理】设A为n元集，R是A上的关系，则存在自然数s和t，使得$R^s = R^t$

合成关系的矩阵表示

\[M_{RS} = M_RM_S = [w_{ik}] \quad \text{其中$w_{ik} = \mathop{\lor}\limits_{j=1}^n(u_{ij} \land v_{jk})$}\]

其实就是矩阵乘法

闭包运算

设R是X上的二元关系，如果有另一个关系$R’$满足：

$R’$是自反的(对称的，可传递的)；
$R \subseteq R’$
对任何自反的（对称的，可传递的）关系$R’’$，如果有$R \subseteq R’’$，就有$R’ \subseteq R’’$，则称关系$R’$为R的自反（对称，传递）闭包。记为$r(R), (s(R), t(R))$。

口语描述：自反闭包是包含关系R的最小的自反关系R’

设R是X上的二元关系，如果：

R是自反的，当且仅当r(R) = R
R是对称的，当且仅当s(R) = R
R是传递的，当且仅当t(R) = R

设R是X上的二元关系，则$r(R) = R \cup Ix$

Note: 设Ix是X上的二元关系，且满足$Ix=\{<x,x>∣x∈X\}$，则称Ix(或 Ex)是X上的相等关系。

设R是X上的二元关系，则$s(R) = R \cup \tilde R$

设R是X上的二元关系，则$t(R) = \mathop{\cup} \limits_{i=1}^\infty R^i = R \cup R^2 \cup R^3 \cup …$

证明：

（1）$r(R) = R \cup I_A$

法一：互为子集法

法二：定义法，令$R’ = R \cup I_A$

$R \cup I_A \subseteq R’$
R’自反
设$\exists R’‘(R \subseteq R’’, R’‘自反)$
$R \subseteq R’, R \subseteq R’’$
$R’‘自反 \Rightarrow I_A \subseteq R’’$ $R’ \subseteq R’’$

感觉这里不对，这只能证明有比它大的，证明不了它最小

（2）$s(R) = R \cup R^{-1}$

法一：互为子集法

法二：

$R \cup R’$
$R’对称$
$\forall x R’ y, \quad <x, y> \in R \cup R^{-1} \quad 要证<y, x> \in R \cup R^{-1}$
$若<x, y> \in R, 则<y, x> \in R^{-1}, <y, x> \in R’$
$若<x, y> \in R^{-1}，则<y, x> \in R, <y, x> \in R’$
对称性得证
证明最小，同上（还是对这里有困惑）

（3） $t(R) = R \cup R^2 \cup R^3 \cup …$

定义法：令$R’ = R \cup R^2 \cup …$

$R \subseteq R’$
$R’$是传递关系（目标：$<x, z> \in R’$）
$\forall <x, y> \in R’, <y, z> \in R’$
即$<x, y> \in R \cup R^2 \cup …$
$<y, z> \in R \cup R^2 \cup…$
$\exists m, n，使得 <x, y> \in R^m, <y, z> \in R^n$
$\Rightarrow <x, z> \in R^{m + n}$
设$R’‘(R \subseteq R’’, 传递)$
要证：$R’ \subseteq R’’$
$R’ = R \cup R^2 \cup …$
只需证$\forall i \in N, R^i \subseteq R’’$
设$<x, y> \in R^i$ (要证$<x, y> \in R’’$)
$\exists z_1, z_2, …, z_{i-1} \in A$
使得$<x, z_1> \in R, <z_1, z_2> \in R, …, <z_{i-1}, y> \in R$
$\Rightarrow <x, z_1> \in R’’, <z_1, z_2> \in R’’, …, <z_{i-1}, y> \in R’’$
$R’‘$传递， $<x, y> \in R’’$

例子：

【计算题】$X = \{1, 2, 3, 4\}$， R是集合X上的二元关系
$R = \{<1, 2>, <2, 1>, <2, 3>, <3, 4>\}$。
求$r(R), s(R), t(R)$

解：

\[r(R) = R \cup I_A = \{<1, 2>, <2, 1>, <2, 3>, <3, 4>, <1, 1>, <2, 2>, <3, 3>, <4, 4>\}\] \[s(R) = R \cup R^{-1} = \{<1, 2>, <2, 1>, <2, 3>, <3, 4>, <3, 2>, <4, 3>\}\]

$t(R) = R \cup R^2 \cup R^3 \cup R^4$
$M_{t(R)} = M_R \lor M_{R^2} \lor M_{R^3} \lor M_{R^4}$

判断关系性质的充要条件

【定理】设R为A上的关系，则

R在A上自反当且仅当 $I_A \subseteq R$
R在A上反自反当且仅当 $R \cap I_A = \phi$
若对于X中的每个x，有$x \not R x$，则称二元关系R是反自反的
R在A上对称当且仅当 $R = R^{-1}$
R在A上反对称当且仅当 $R \cap R^{-1} \subseteq I_A$
R在A上传递当且仅当 $RR \subseteq R$

传递的条件可改为 $R^n \subseteq R, \forall n = 1, 2, 3…$

	自反闭包	对称闭包	传递闭包
I上的小于关系<	$\leq$	$\neq$	$<$
I上的小于等于关系$\leq$	$\leq$	$U$	$leq$
全域关系U	U	U	U
I上的不等于关系$\neq$	U	$\neq$	U

设X是含有n个元素的集合，R是X上的二元关系，则存在一个正整数k≤n，使得t(R)=R∪R2∪R3∪…∪Rk。

于是，在n个元素的有限集上关系R的传递闭包可以写为t(R)=R∪R2∪R3∪…∪Rn。

如果R是自反的，那么s(R)和t(R)都是自反的
如果R是对称的，那么r(R)和t(R)都是对称的
如果R是传递的，那么r(R)是传递的

关系R的自反，对称，传递闭包还可以进一步复合，有如下定理：

设X是集合，R是X上的二元关系，则

rs(R) = sr(R)
rt(R) = tr(R)
st(R) = ts(R)

Warshall算法

设R为有限集X上的二元关系， $\mid X \mid=n$， M为R的关系矩阵，可如下求取$R^+$的关系矩阵 A：

置新矩阵A：＝M
置 i：＝1；
对所有的j如果A[j，i]＝1，则对k＝1，2，… ，n A[j，k]：＝A[j，k]+A[i，k]；（就是两行进行逻辑加运算）
i加1；
如果i≤n，则转到步骤(3)，否则停止。

等价关系

划分：一个集合划分为若干个子集，这些子集两两不相交。

【定义】设R为非空集合上的关系。若R是自反的、对称的和传递的，则称R为A上的等价关系。设R是一个等价关系，则$<x, y> \in R$，称x等价于y，记作x-y。

三角形相似
集合相等
等值

等价类：

【定义】设R为非空集合A上的等价关系， $\forall x \in A$，令

\[[x]_R = \{y \mid y \in A \land x R y\}\]

称$[x]_R$为x关于R的等价类，简称为x的等价类，简记为[x]

口语描述：在集合A中，所有和x等价的y 构成的集合。其中包含x。

那么反过来，在集合A中，所有和y等价的x构成的集合，它们其实是一样的。

Note：等价类从划分的角度来讲，就是一个一个的划分块

【定理】设R为非空集合A上的等价关系，则

$\forall x \in A$，[x]是A的非空子集
$\forall x, y \in A$，如果xRy，则[x] =[y]
$\forall x, y \in A$，如果$x \not R y$，则[x]与[y]不交。
$\cup\{[x] \mid x \in A\}= A$，即所有等价类的并集就是A

商集

【定义】设R为非空集合A上的等价关系，以R的所有等价类为元素的集合称为A关于R的商集，记作A/R， $A/R = \{[x]_R \mid x \in A\}$

商集其实就是所有划分块的集合。

【定理】

商集$A/R$就是A的一个划分；
任给A的一个划分$\pi$，如下定义A上的关系R： $R = \{<x, y> \mid x, y \in A \land x与y在\pi的同一划分块中\}$ 则R为A上的等价关系，且该等价关系确定的商集就是$\pi$

例子：

【计算题】设$X = \{1, 2, 3, 4\}$， X的划分$S = \{\{1\}, \{2, 3\}, \{4\}\}$，试写出S导出的等价关系R。

解：

\[R = \{<1, 1>, <2, 2>, <2, 3>, <3, 2>, <3, 3>, <4, 4>\}\]

【计算题】$X = \{1， 2， 3， 4， 5\}，\\ R = \{<1, 2>, <2, 3>, <2, 1>, <1, 3>, <3, 2>, <4, 4>, <5, 5>\}$

求划分块（商集）

解：

\[\pi = A/R = \{\{1, 2, 3\}, \{4\}, \{5\}\}\]

次序关系

设A是一个集合，如果A上的一个关系R，满足自反性、反对称性和传递性，则称R是A上的一个偏序关系，记为“≤”。序偶<A,≤>称为偏序集。

x与y可比: 设R为非空集合A上的偏序关系 $x, y \in A， x与y可比\Leftrightarrow$ $x \leq y \lor y \leq x$

结论：任取两个元素x和y，可能有下述情况：

x<y或（y<x）, x = y， x与y不是可比的

这个可比什么意思？必须是偏序关系中的x，y，不能任取？

全序关系：

R为非空集合A上的偏序， $\forall x, y \in A$， x与y都是可比的，则称为R的全序（或线序）

例：

整数上的小于或等于关系是全序关系

整除关系不是正整数集合上的全序关系

覆盖：

【定义】在偏序集<A,≤>中，如果x,y∈A，x≤y，x≠y且没有其它元素z满足x≤z，z≤y，则称元素y盖住元素x。

\[COV A=\{<x,y> \mid x,y∈A且y盖住x\}\]

即唯一比x大的只有y

盖住元素不唯一
盖住元素可能不存在

偏序关系图－哈斯图

用小圆圈代表元素
如果x≤y，且x≠y，则将代表y的小圆圈画在代表x的小圆圈之上
如果<x,y>∈COV A，则在x与y之间用直线相连。

极大元素和极小元素

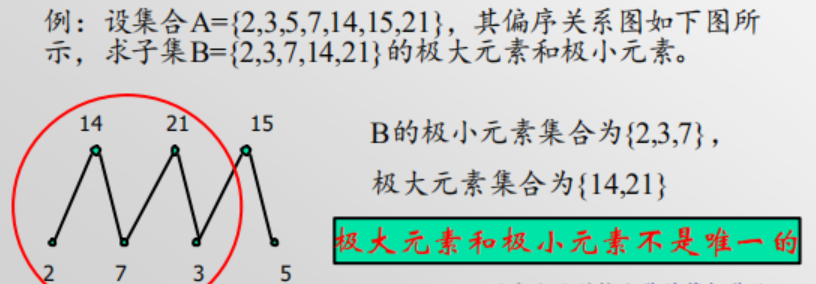
极大极小是小于

极小：在子集B中，不存在x，使得x小于y

极大：在子集B中，不存在x，使得x大于y

最大元素和最小元素

最大最小是小于等于

最大：在子集B中，对任意x，y大于等于x

最小：在子集B中，对任意x，y小于等于x

例子：

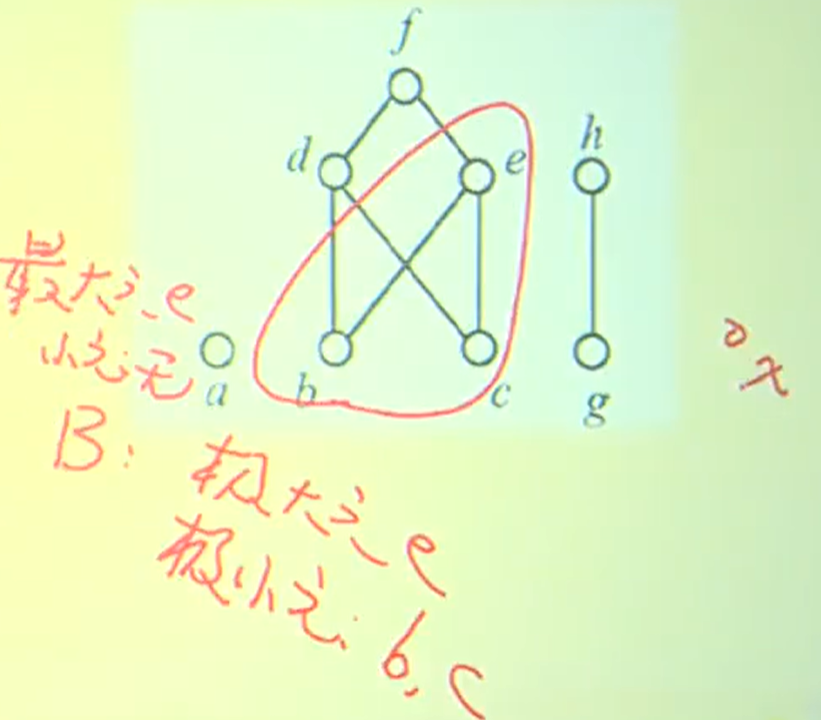
在这个例子中，子集B中，b之所以不是最小元，因为b和c既不是小于关系，也不是等于关系

b之所以是极小元，因为不存在其它元素比b小

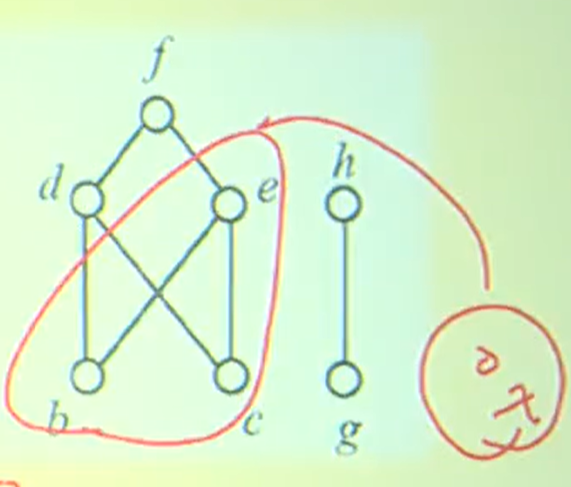
在这个例子中，子集B加入了孤立节点x

对于子集B，对于x，它既不比e大，也不等于e，所以不存在最大值。

上下界

格

偏序集中所有子集都有最大下界和最小上界，称为格。

其中有补分配格称为布尔代数（有补，分配，有界）。

函数

函数的复合是右复合

例子：

题

离散数学–通路数的矩阵计算法

所谓矩阵计算法，实际上就是把一个图用邻接矩阵表示，

我们记为A，那么 A^M上对应(i,j)的值就是i通过M条边到达j的方案数，

理解：当n = 1是显然成立

当 n >= 2时，假设当 n= k时结论成立

那么当 n = k+1是，

A^k+1 = A ^ k * A

有矩阵乘法可知，A（i,j）k+1 = sigma[ A（i,t)1 * A(t，j)k ]

实际上就是i经过t到达j方案数，

由乘法原理知，A^k+1表示的就是进过K+1条边的方案数。。

集合