模拟信号和数字信号
Q:打电话时电话线里传递的信号是模拟还是数字信号?
A:电话线里传输的是模拟信号
Q:用ADSL上网时电话线里传递的信号呢?
A:数字信号
Q:以太网双绞线里传递的信号呢?
A:是模拟信号,是已经经过调制的模拟信号。
Q:WIFI空中传播的信号?
A:无线发射和接收的都是高频正弦波信号,属于模拟信号。
Q:手机在空中传递的信号?
A:模拟信号。
Q:收音机空中的信号?
A:模拟信号。
模拟信号
正弦波
周期模拟信号可以分为简单类型或复合类型两种。
简单类型模拟信号,即正弦波(sine wave),不能再分解为更简单的信号,而复合型模拟信号则是由多个正弦波信号组成的。
决定正弦波的三个参数:峰值振幅、频率和相位
\[s(t) = Asin(2 \pi ft + \phi)\]均方根(rms)值
均方根值也称作为效值,它的计算方法是先平方、再平均、然后开方。
比如幅度为100V而占空比为0.5的方波信号,如果按平均值计算,它的电压只有50V,而按均方根值计算则有70.71V。
这是为什么呢?
举一个例子,有一组100伏的电池组,每次供电10分钟之后停10分钟,也就是说占空比为一半。如果这组电池带动的是10Ω电阻,供电的10分钟产生10A的电流和1000W的功率,停电时电流和功率为零。那么在20分钟的一个周期内其平均功率为500W,这相当于70.71V的直流电向10Ω电阻供电所产生的功率。而50V直流电压向10Ω电阻供电只能产生的250W的功率。
Q:中国民用电压有效值?峰值振幅?
A:
中国民用电压的峰值是311V 有效值是220V
311 V=220V*1.414 220V
对于直流,有效值等于平均值等于峰值
对于正弦交流,有效值等于1.1倍平均值,等于0.707倍峰值.
对于任意波形(包括直流),有效值满足均方根关系.即:瞬间电压的平方在一个周>期内的积分的平方根再除以时间.
波长和周期
\[波长 = 传播速度 \times 周期\]带宽
复合信号的带宽是信号最高频率与最低频率 的差值(即所包含的频率范围)。
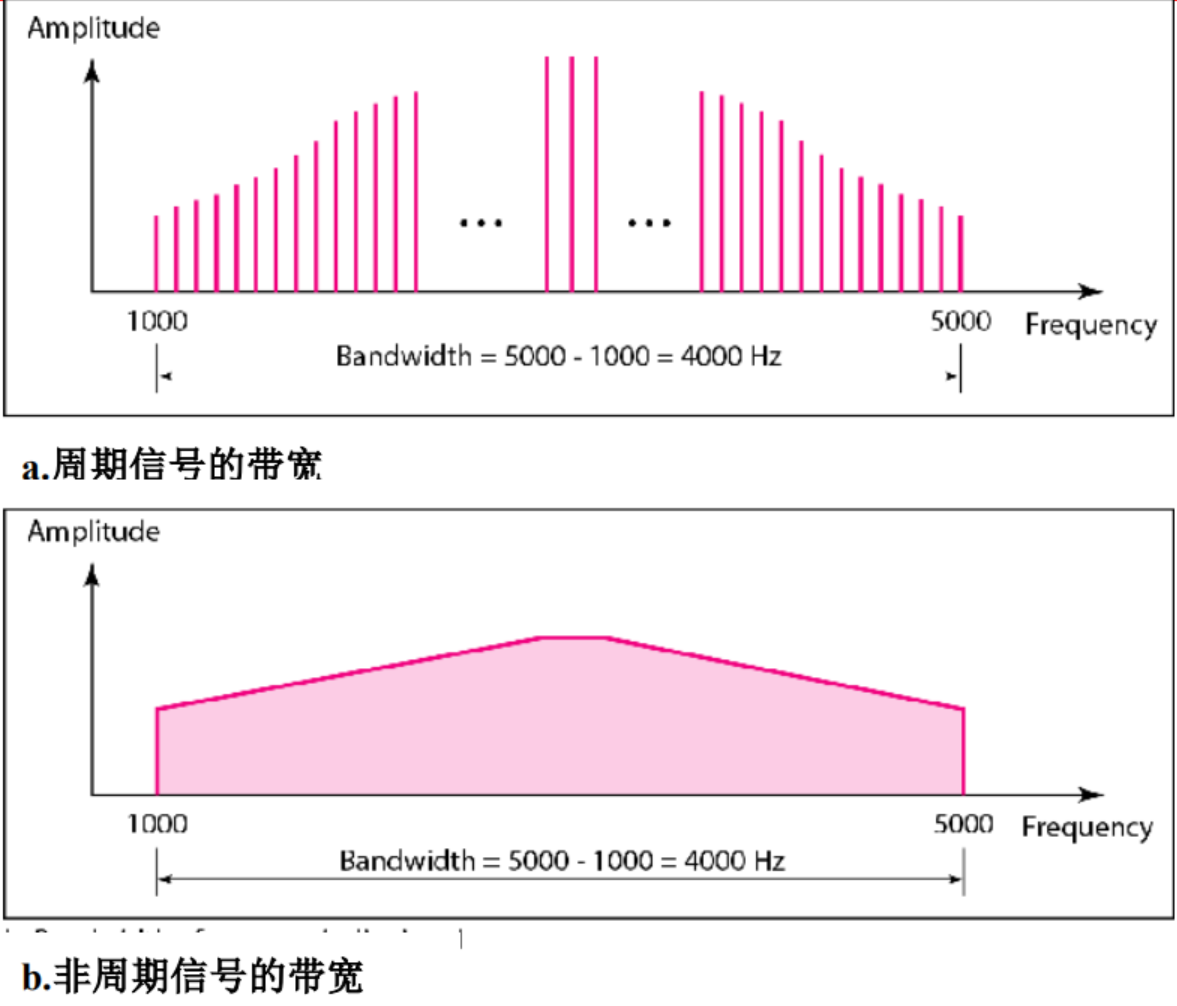
例子:
非周期复合信号的另一个例子是老式模拟黑白电视接收的信号。电视屏幕由像素组成。如果我们假定分辨 率为525×700,那么每个屏幕就会有367,500个像素。 如果屏幕每秒扫描30次,每秒就是367,500×30=11,025,000个像素。最坏的情况是黑色像素和白色像素交替。每个周期我们能发送两个像素。因此,每秒我们需要11,025,000 / 2 = 5,512,500个周期(或Hz)。所需的带宽是5.5125 MHz。
数字信号
一个数字信号有8个电平,那么每个电平需要多少个位表示?我们根据下面公式进行计算:
\[\text{Number of bits per level} = log_2 8 = 3\]每个信号电平用3位表示
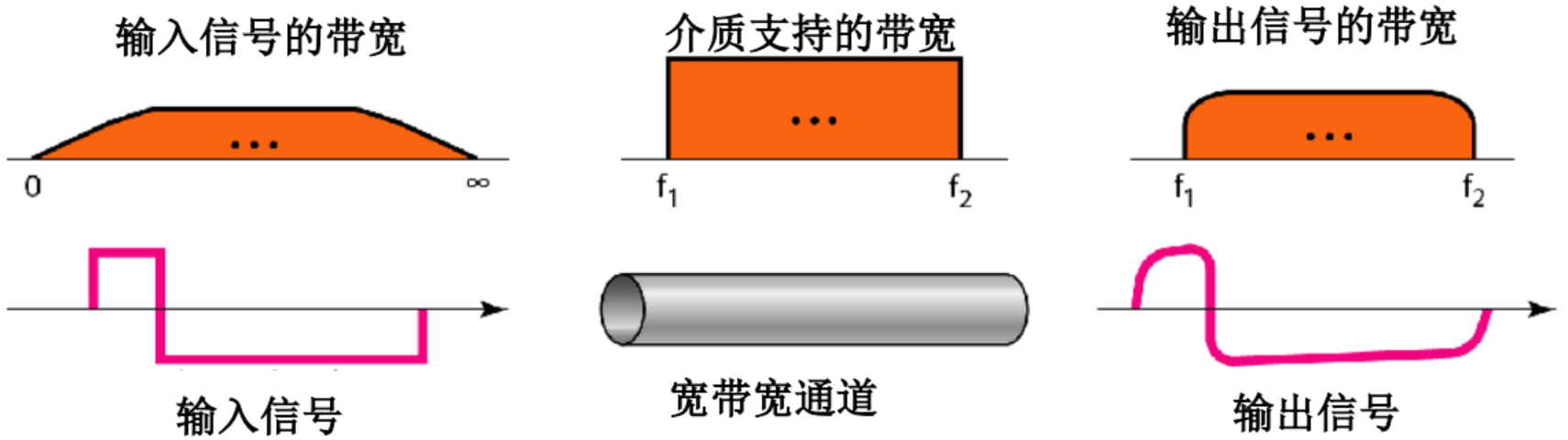
- 基于傅立叶分析,数字信号是复合模拟信号,带宽无穷大
- 如果数字信号是周期性的,分解后的信号可以表示为无穷大带宽和离散频率的频域
- 如果数字信号是非周期性的,分解后的信号仍然是无穷大带宽,但频率是连续的
数字信号的传输
- 数字信号是无穷大带宽的复合模拟信号;
- 两种传输方式:基带传输和宽带传输(使用调制);
- 基带传输(以信号本身的频谱进行传输):通过通道发送数字信号,该信号不转换成模拟信号,它需要一个带宽下限频率为0的低通通道(带宽从频率0开始);
- 宽带传输:把数字信号转换成模拟信号进行传输,允许使用带通通道,即带宽不从频率0开始的通道。
基带传输
带宽只组成一条通道的专用介质,例如连接两台计算机的电缆;
例子:
专用通道(介质的整个带宽用于一条单通道)的一个例子是LAN。几乎现在的每一个有线LAN使用专用通 道用于两个站之间的互相通信。在多点连接的总线拓扑结构LAN中,每个时刻只有两个站可以互相通信(时间共享),而其他站限制发送数据。在星型拓扑结构LAN中,每个站和集线器(或交换机)之间的整个通道用于这两个实体间的通信。
基带传输中,所需的带宽与比特率成正比; 如果我们需要更快地发送位,我们就需要更大的带宽。
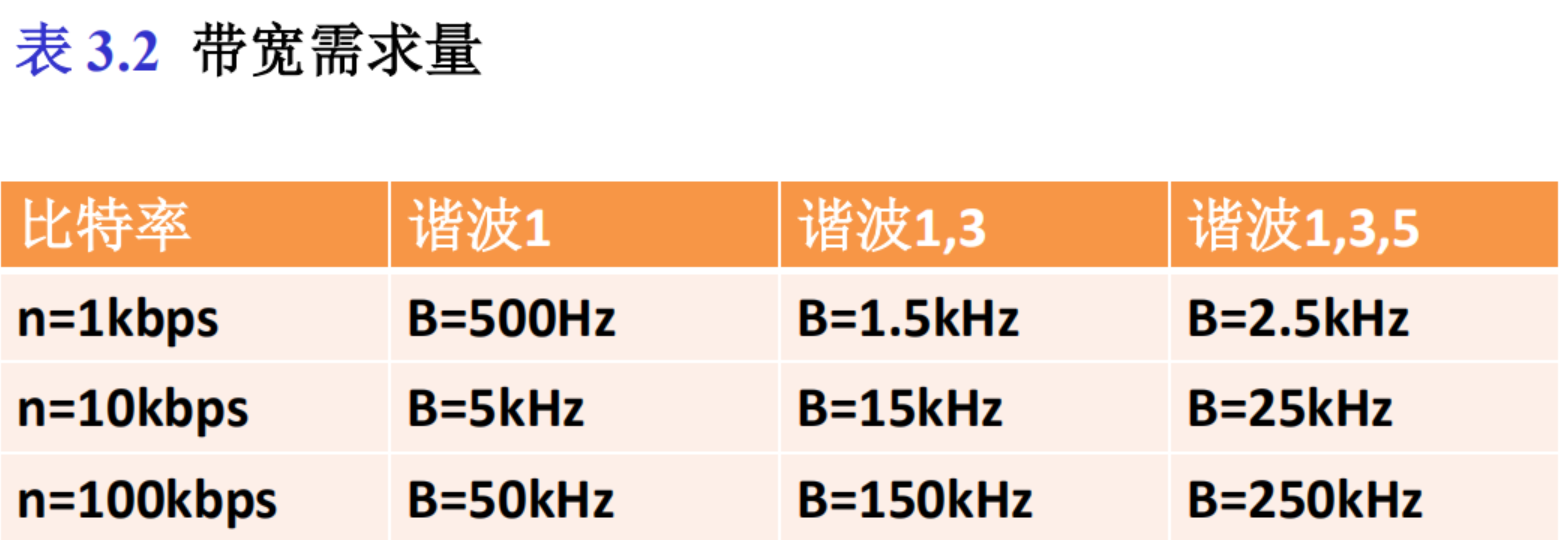
如果我们需要使用基带传输发送 1Mbps,那么低通通道所需的带宽是多少?
解:
答案取决于所需的准确性。 a. 最小带宽、大致近似时,B = 比特率/2,即500 kHz。
b. 使用第一和第三谐波可以得到更好的结果,所需带宽是B = 3 × 500 kHz = 1.5 MHz。
c. 使用第一、第三和第五谐波仍然可以得到更好的结果 ,所需带宽是 B = 5 × 500 kHz = 2.5 MHz。
我们有一条带宽为100kHz的低通通道,那么这条通 道的最大比特率是多少?
解: 如果我们使用第一谐波可以得到最大比特率,比特率是2倍有效带宽,即200kbps。
思考:为什么?
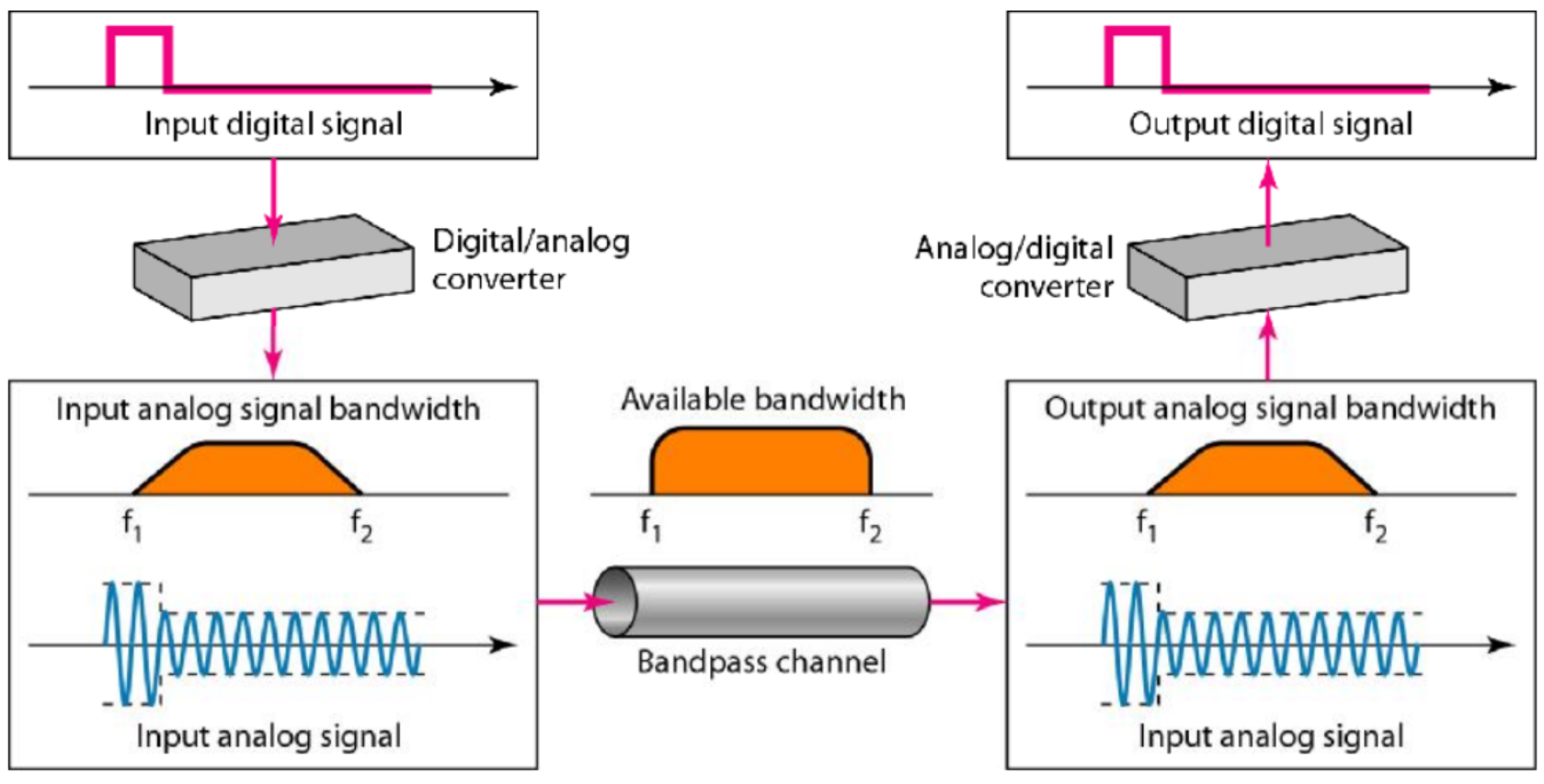
带通通道
如果可用通道是带通通道,我们不能直接发送数字信号到通道;我们需要在传输前把数字信号转换成模拟信号。
例子:
使用调制的宽带传输的一个例子是通过电话用户线传输计算机数据,电话用户线连接住所到中心电话局。这些线路设计用有限带宽承载语音。这个通道通常被看做带通通道。我们从计算机把数字信号转换成模拟信号,然后发送模拟信号。我们要安装两个转换器用来在发送端把数字信号转换成模拟信号以及在接收端 把模拟信号转换回数字信号。在这种情况下,转换器 称为调制解调器。
第二个例子是数字蜂窝电话。为了更好地接收,数字蜂窝电话把模拟信号转换成数字信号(见第16章)。虽然分配给公司提供数字蜂窝电话服务的带宽很广, 但是我们不能不经转换发送数字信号。原因是,我们在主叫方和被叫方之间只有一条可用的带通通道。我们需要在发送前把数字信号转换成复合模拟信号。
传输减损
通常会发生三种类型的减损:衰减、失真和噪声。
衰减
分贝
分贝(decibel,dB)用于计算两种信号之间或者同一信号在两个不同位置之间的相对强度:
\[dB = 10 log_{10} \frac{P2}{P1}\]P1和P2分别是信号在位置1和位置2的功率
例子:
假设信号通过一种传输介质传输后,它的功率降低了 一半。这可以表示为P2=(1/2)P1,这种情况下衰减(损失的能量)可以计算为:
\[10 log_{10} \frac{P_2}{P_1} = 10 log_{10} \frac{0.5P_1}{P_1} = 10(-0.3) = -3dB\]–3dB(分贝)或者3dB衰减等价于功率损失了一半。
工程人员使用分贝来计算信号强度变化的原因之一是,当涉及计量多处(级联)而不仅仅是两处的信号强度时,分贝数可以相加(或相减)。在图3.27中,一个信号从位置1传输到位置4,在这种情况下,分贝可 以计算为:
\[dB = -3 + 7 - 3 = +1\]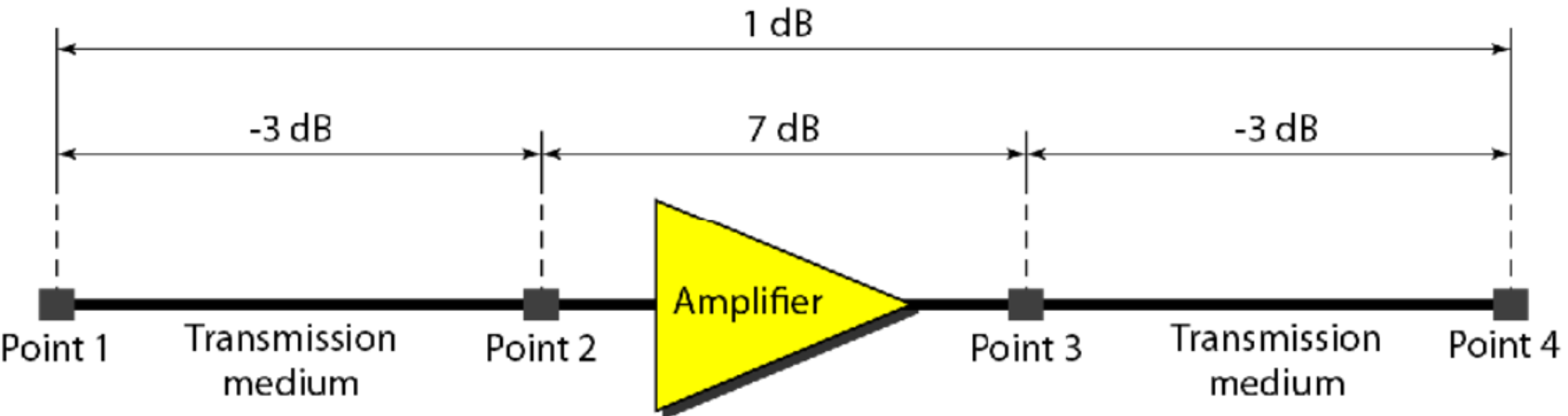
dB~m~
有时候分贝用来以毫瓦计量信号功率。这种情况下,它成为dBm,计算为dBm = 10log10Pm , 这里Pm是以毫 瓦为单位的功率。
如果信号的dBm=−30,计算它的功率:
\[dB_m = 10 log_{10} P_m = -30 \\ log_{10} P_m = -3 \quad P_m = 10^{-3}mW\]每公里每分贝数dB/km
电缆中的损耗一般定义为每公里分贝数(dB/km)。
例子:
如果电缆每公里分贝数为−0.3dB/km,信号在电缆开始端的功率为2mW,则在5km处信号的功率是多少?
解:
电缆中的损耗为:
\[5 \times (-0.3) = -1.5 dB\]计算功率如下:
\[dB = 10 log_{10} \frac{P_2}{P_1} = -1.5 \\ \frac{P_2}{P_1} = 10^{-0.15} = 0.71 \\ P_2 = 0.71 P_1 = 0.7 \times 2 = 1.4mW\]失真
- 失真意味着信号改变了形态或形状;
- 导向媒体上信号传播速度随频率的不同而改变
- 各信号成分延迟的差异会产生相位的差异,即接收 方的信号成分与发送方的信号成分存在相位差异
噪声
噪声包括:热噪声、感应噪声、串扰、脉冲噪声。
信噪比
信噪比:信号功率与噪声功率的比率,较高意味着信号较少的被噪声破坏,较低意味着被噪声较多的破坏
\[SNR = \frac{平均信号功率}{平均噪声功率}\]以分贝描述:
\[SNR_{dB} = 10 log_{10}SNR\]例子:
信号的功率是10mW,噪声的功率是1μW,那么SNR和SNR~dB~是多少?
\[SNR = \frac{10000 \mu W}{1 \mu W} = 10000 \\ SNR_{dB} = 10 log_{10}10000 = 10 log_{10} 10^4 = 40\]对于无噪声通道的SNR和SNRdB是
\[SNR = \frac{signal power}{0} = \infty \\ SNR_{dB} = 10 log_{10} \infty = \infty\]在现实中不会得到这样的比率,它是理论上的。
数据速率的限制
两个理论上的定理或公式用于计算数据速率:
- 无噪声通道:奈奎斯特定理
- 噪声通道:香农容量公式
奈奎斯特定理
对于无噪声通道,奈奎斯特定理定义了理论上的最 大比特率:
\[比特率 = 2 \times 带宽 \times log_2 L\]其中,带宽指通道的带宽, L表示信号电平的个数
Note: 增加信号电平数会增加接收方的负担,减弱系统的可靠性。
奈奎斯特公式是否适用于基带传输中描述的直觉上的比特率?
当只有两个电平时它们匹配。我们说,在基带传输中,如果我们在最坏情况只使用第一谐波,那么比特率是2倍带宽。但是,奈奎斯特公式比我们直觉上得到的更通用,它可以应用到基带传输和调制,也可以应 用到有两个或多个信号电平的情况。
香农容量公式
对于噪声通道,香农容量公式定义了理论上的最高数据速率。
Note: 公式没有指出信号电平数,定义了通道特性;
\[通道容量 = 带宽 \times log_2 (1+SNR)\]其中,带宽指通道的带宽, SNR是信噪比
为了实际操作方便,当SNR很大时,假定SNR + 1几 乎与SNR相等,理论通道容量可以简化为:
\[C = B \times \frac{SNR_{dB}}{3}\]例子:
有一个1MHz带宽的通道,通道的信噪比是63,合适的比特率以及信号电平是多少?
解:
首先, 使用香农公式确定上限: \(SNR = 63, B = 10^6 Hz \\ C = B \times log_2 (1+SNR) = 10^6 \times log_2 64 = 6Mbps\)
尽管香农公式计算结果是6Mbps, 但这是上限。 为了获得更好地性能, 可选择一些低一些的值, 如4Mbps。
然后使用奈奎斯特公式计算信号电平的数量:
\[4Mbps = 2 \times 1MHz \times log_2 L \Rightarrow L = 4\]Note: 香农容量公式给出数据速率的上限,奈奎斯 特定理给出所需的信号电平数。
性能
带宽
带宽:以赫兹或比特率表示;
Note:在网络中,带宽具有两种不同的含义
- 以赫兹衡量的带宽指复合信号包含的 频率范围或者通道能通过的频率范围;
- 以每秒比特数衡量的带宽指通道或链 路中位传输的速率。
吞吐量
吞吐量:发送速度快慢的实际衡量值,小于带宽;
例子:
带宽为10Mbps的网络每分钟只能平均传输12,000个帧 ,每个帧平均携带10,000个位。那么这个网络的吞吐量是多少?
解:
吞吐量为:
\[\frac{12000 \times 10000}{60} = 2Mbps\]延迟
延迟:第一个比特从源开始发出到整个报文完全到达目标所经历的时间,包括传播时间(与介质相关)、传输时间(与报文长度和带宽有关)、排队时间和处理延迟;
例子:
如果网络的带宽是1Gbps,那么2500个字节的报文( 一封电子邮件)的传播时间和传输时间是多少?假定发送方和接收方之间的距离是12,000km,光以速度 $2.4×10^8m/s$传输。
解:
传输时间:
\[\text{Transmission time} = \frac{2500 \times 8}{1 \times 10^9} = 2 \times 10^{-5}s\]传输时间:
\[\text{Propagation time}= \frac{12000 \times 1000}{2.4 \times 10^8} = 0.05s\]带宽与延迟的乘积
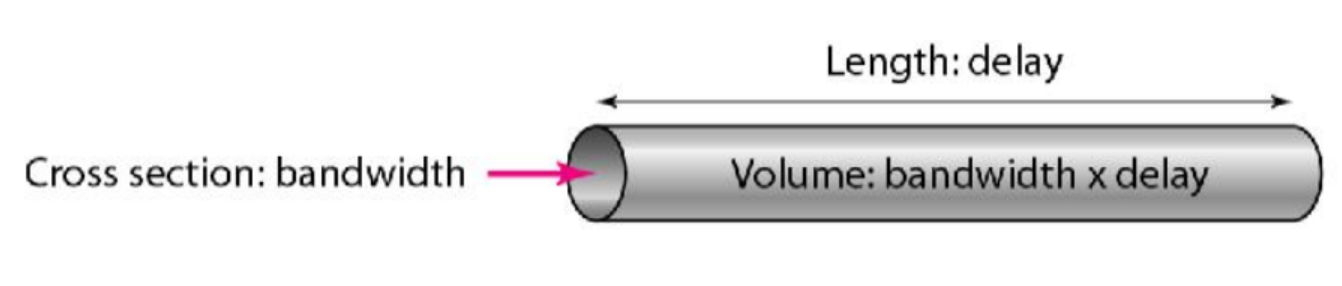
带宽与延迟的乘积:定义了充满链路的位数;
我们把两点间的链路看做管道。管道的横截面表示带 宽,管道的长度表示延迟。我们可以说管道的容量定 义了带宽延迟乘积,如下图所示。
抖动
抖动:不同分组有不同的延迟,某些应用敏感
数字传输
数据元素和信号元素
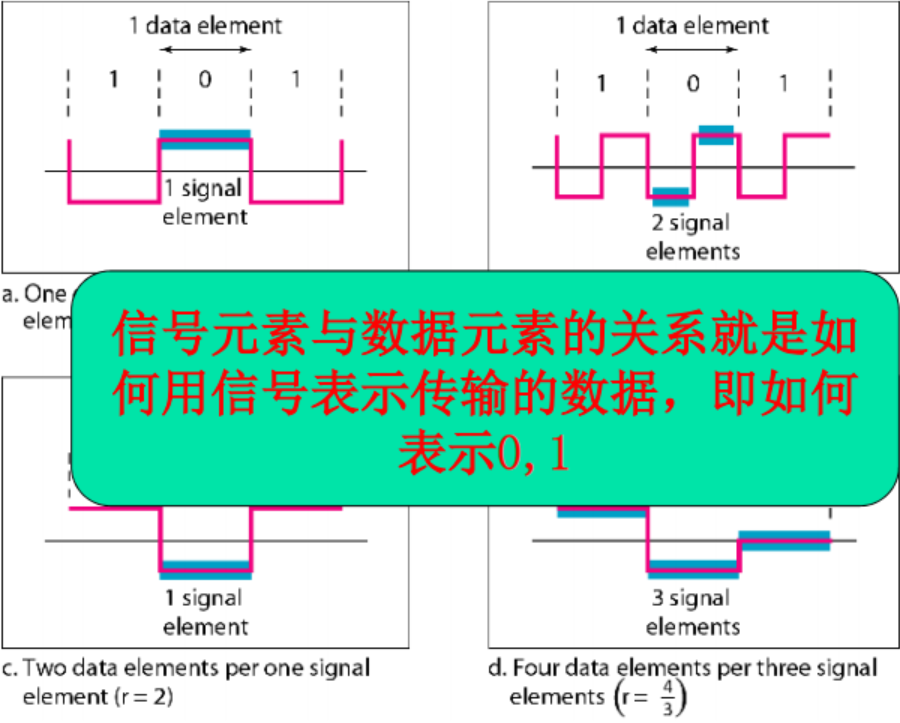
数据元素(data element):表示一块信息的最小实体 ,即位(bit),是我们需要发送的,被承载的;
信号元素(signal element):是数字信号的最小单元 ,承载数据单元,是我们能发送的,是传输载体;
定义r为每个信号元素承载的数据元素的数量:
- 如果一个数据元素被一个信号元素承载,则r = 1
- 如果一个信号元素承载两个数据元素,则r = 2
- 如果两个信号元素承载一个数据元素,则r = 1/2
- 如果三个信号元素承载四个数据元素,则r = 4/3
数据速率和信号速率
数据速率:每秒钟发送的数据元素(位)的数量, 单位是bps(bits per second),也叫比特率;
信号速率:每秒钟发送的信号元素的数量(准确说法:信号电平发生改变或被调制的速率),单位是波特率(baud),或者叫做 或者叫做脉冲速率(pulse rate)、调制速率(modulation rate)。
数据通信的一个目标:增加数据速率(增加了传输速度)而降低信号速率(降低了带宽要求,应该说是波特率而不是比特率决定了数字信号的带宽)
数据速率与信号速率的关系
\[S = c \times N \times \frac{1}{r} baud\]- N: 数据速率, 单位bps
- c:情形因子(case factor), 会根据情形发生改变
- S:是信号速率
- r:比率
例子:
一个信号携带数据,一个数据元素编码成一个信号元素(r=1)。如果比特率是100kbps,c在0和1之间,那么波特率的平均值是多少?
假设$c = \frac{1}{2}$:
\[S = \frac{1}{2} \times 100000 \times 1 = 50000 = 50 kbaud\]虽然数字信号的真实带宽是无限的,但有效带宽(忽略小振幅成分)是有限的。
- 波特率而不是比特率决定了数字信号的带宽;
- 波特率和带宽是有关系的,成正比;
- 波特率和带宽是有关系的,成正比;
- 最小带宽$B_{min}$与波特率相等;
- 若给定通道带宽B,可以得到最大数据速率$N_{max}$
例子:
通道的最大数据速率是$N_{max} = 2 × B × log_2 L$(由奈奎斯特公式定义),这与前面定义的$N_{max}$公式一致吗?
解:
有L个电平信号, 每个电平可以携带$log_2 L$个比特。 如果每个电平则与一个信号元素对应, 假定一般情形($c = \frac{1}{2}$),则:
\[N_{max} = \frac{1}{c} \times B \times r = 2 \times B \times log_2 L\]基线、基线偏移和直流分量
基线(Baseline):解码数字信号时,接收方计算收到信号功率的运行平均值。输入信号的功率会与基线比较 来确定数据元素的值;
基线偏移(Baseline Wandering):指基线随时间定向的缓慢变化。0或1的长字串会引起基线偏移, 使得接收方不能正确地进行解码,好的线路编码方案需要防止基线偏移。
直流成分:接近于零频率的成分称为直流成分(即常量), 这会给不允许通过
自同步
为了正确解释发送方的信号,接收方的位间隔与发送方的位间隔必须严格对应与匹配
自同步数字信号在传输的数据中包含有定时信息
通常使用信号中包含有提示接收方起始、中间和结束位置的脉冲的跳变(transition)完成自同步
编码方式
单极性不归零NZR
单极:所有电平都在时间轴的一边;
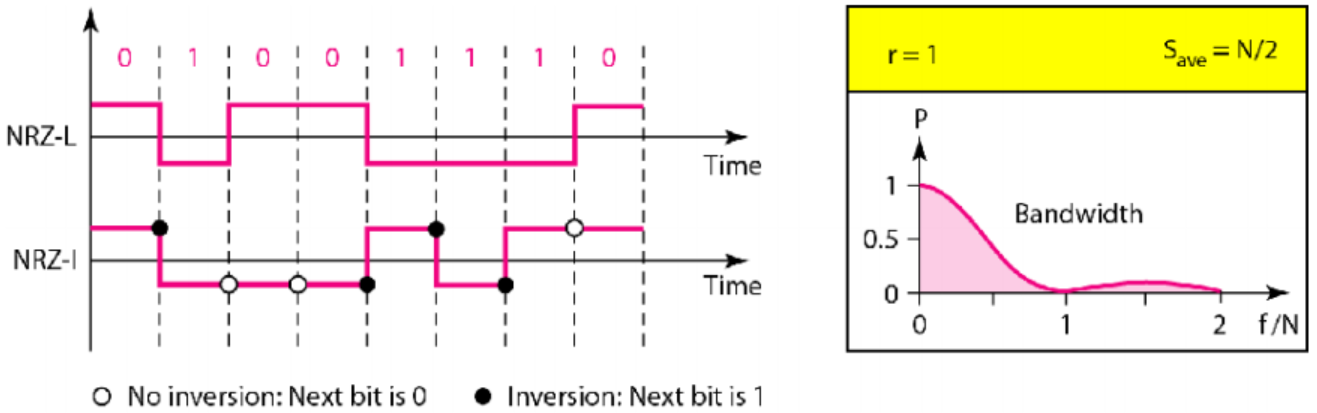
极性NRZ-L方案和极性NRZ-I方案
极性:电平在时间轴的两边;
极性NRZ:信号振幅使用两个电平,有NRZ-L(NRZ电平编码,电平决定位值)和NRZ-I(NRZ反相编码,电平是否跳转决定位值)两种形式。

例子:
系统使用NRZ-I传输10Mbps的数据,试问平均信号速 率和最小带宽是多少?
解:
$c = \frac{1}{2} \quad r = 1$
平均信号速率:
\[S = c \times N \times \frac{1}{r} = \frac{N}{2} = 5M baud\]平均波特率的最小带宽$B_{min} = S = 5MHz$
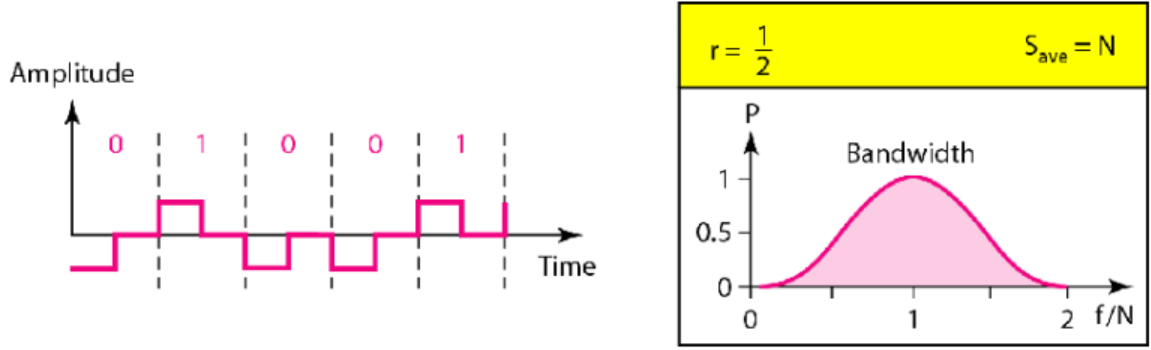
极性RZ(归零)编码方案
NRZ在发送方和接收方时钟不同步时有问题,不知位何时结束,下一位何时开始;
RZ编码在每个位中间信号变为0,解决同步问题;
信号有三个值:正值,负值和零;
极性-双相(biphase)编码
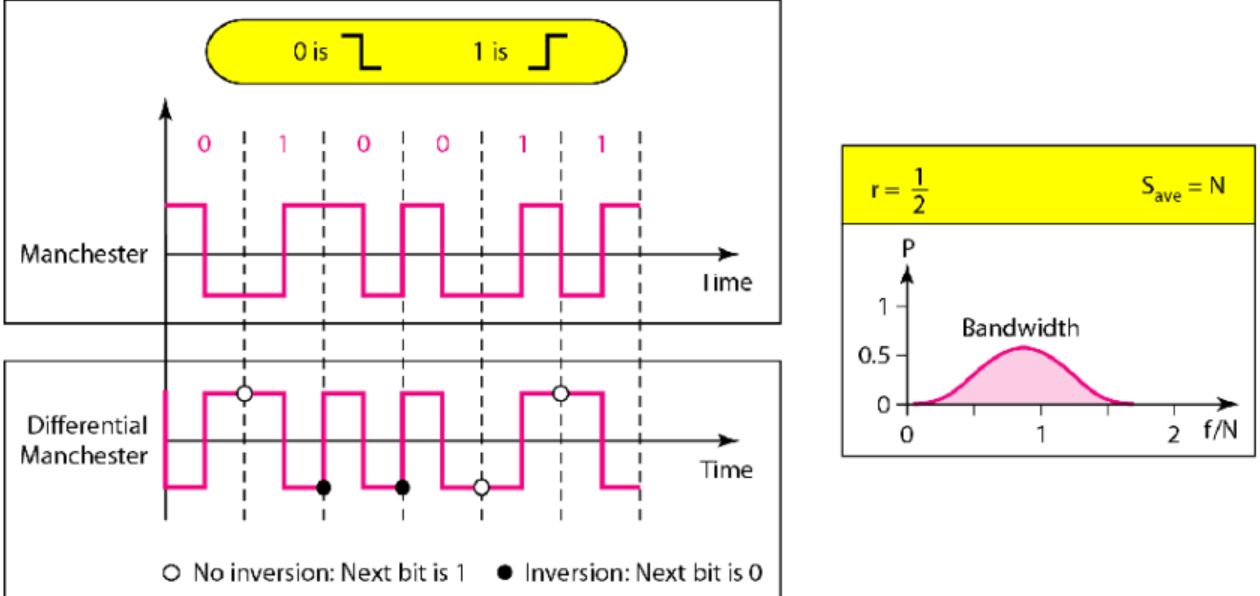
位中间跳变思想:曼彻斯特编码和差分曼彻斯特编码;
曼彻斯特编码:RZ的位中间跳变 + NRZ-L
- 位的持续时间被二等分,前半部分电平保持一个水平,后半部分变成另外一个水平
- 位中间的跳变提供了同步
- 0:由高$\rightarrow$低,1:由低$\rightarrow$高
差分曼彻斯特编码:RZ + NRZ-I
- 中间总有跳变,值在位起始位置确定
- 1:起始没有跳变; 0:起始有跳变

传输介质
有向介质(有线)
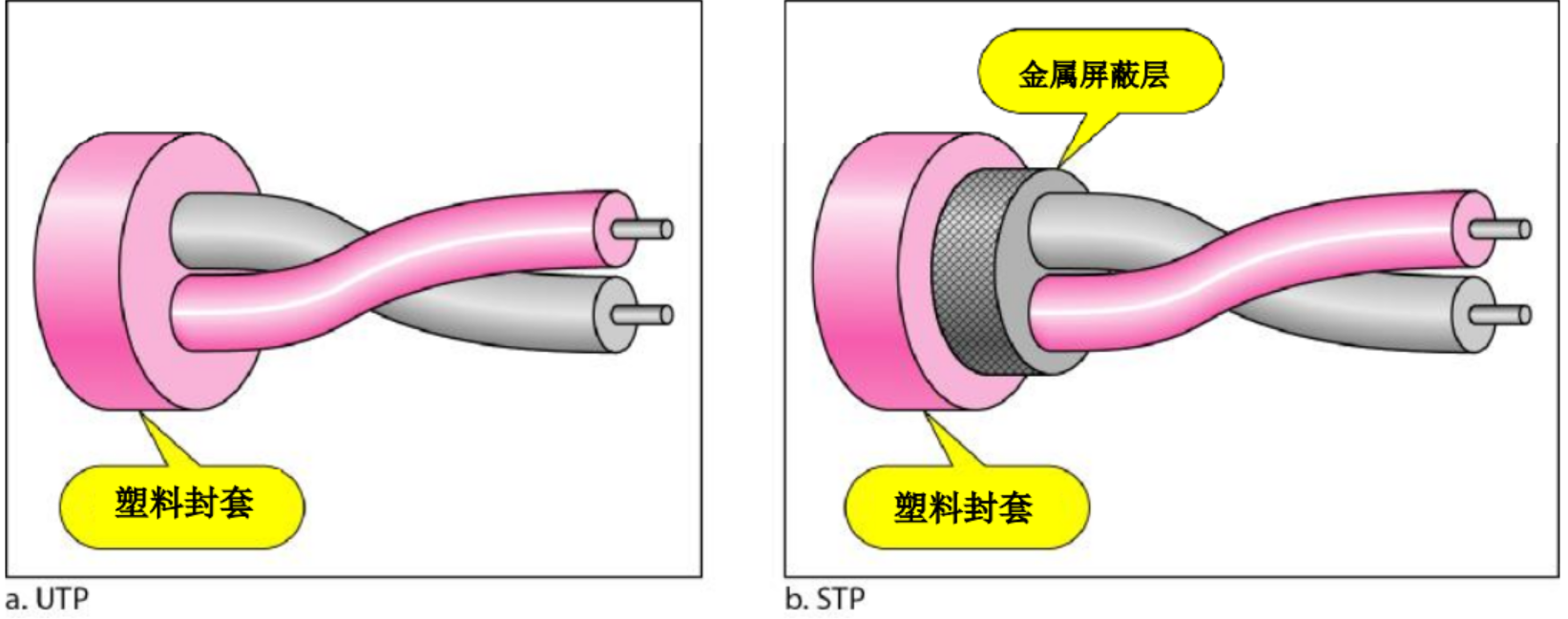
双绞线
非屏蔽双绞线(UTP):unshielded twisted-pair,最常见,价格便宜; 和屏蔽双绞线(STP):shielded twisted-pair,IBM生产,增加了金属屏蔽层,防止噪声或者串扰
3类和5类UTP:
- 3类和5类线缆在局域网应用中受到极大关注;
- 3类对应于话音级线缆,就是那些在大多数办公楼里都大量存在的电缆;只要设计合理且传输距离不远,3类UTP的数据率可达16Mbps;
- 在新建成的办公楼里,越来越常见的预先铺设的电缆是5类UTP;如果传输距离不远且设计合理,5类UTP的数据率可达100Mbps
同轴电缆
同轴电缆-比双绞线传输频率更高(500MHz)
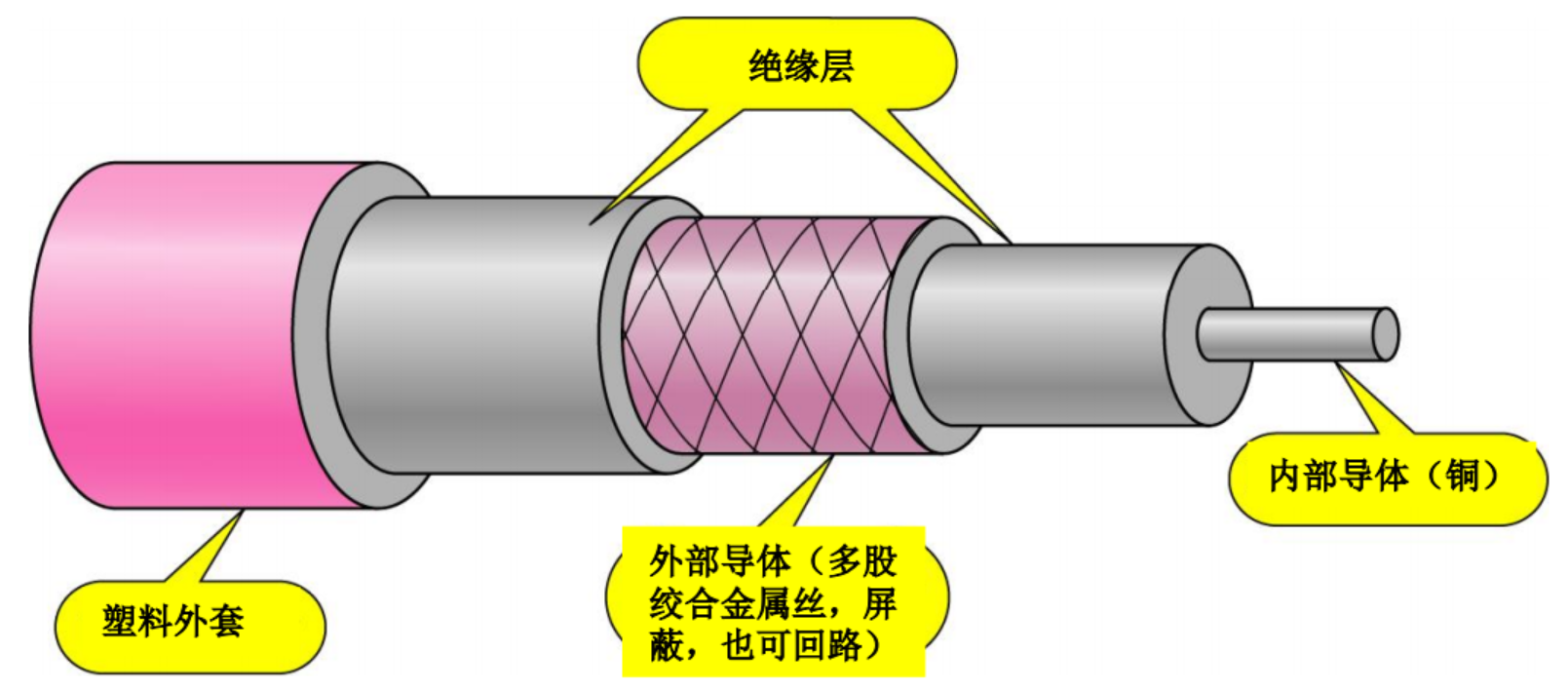
传 统 总 线型以太网 : 10Base2 ( 细缆以太网 ,185m)、10Base5(粗缆以太网,500m)
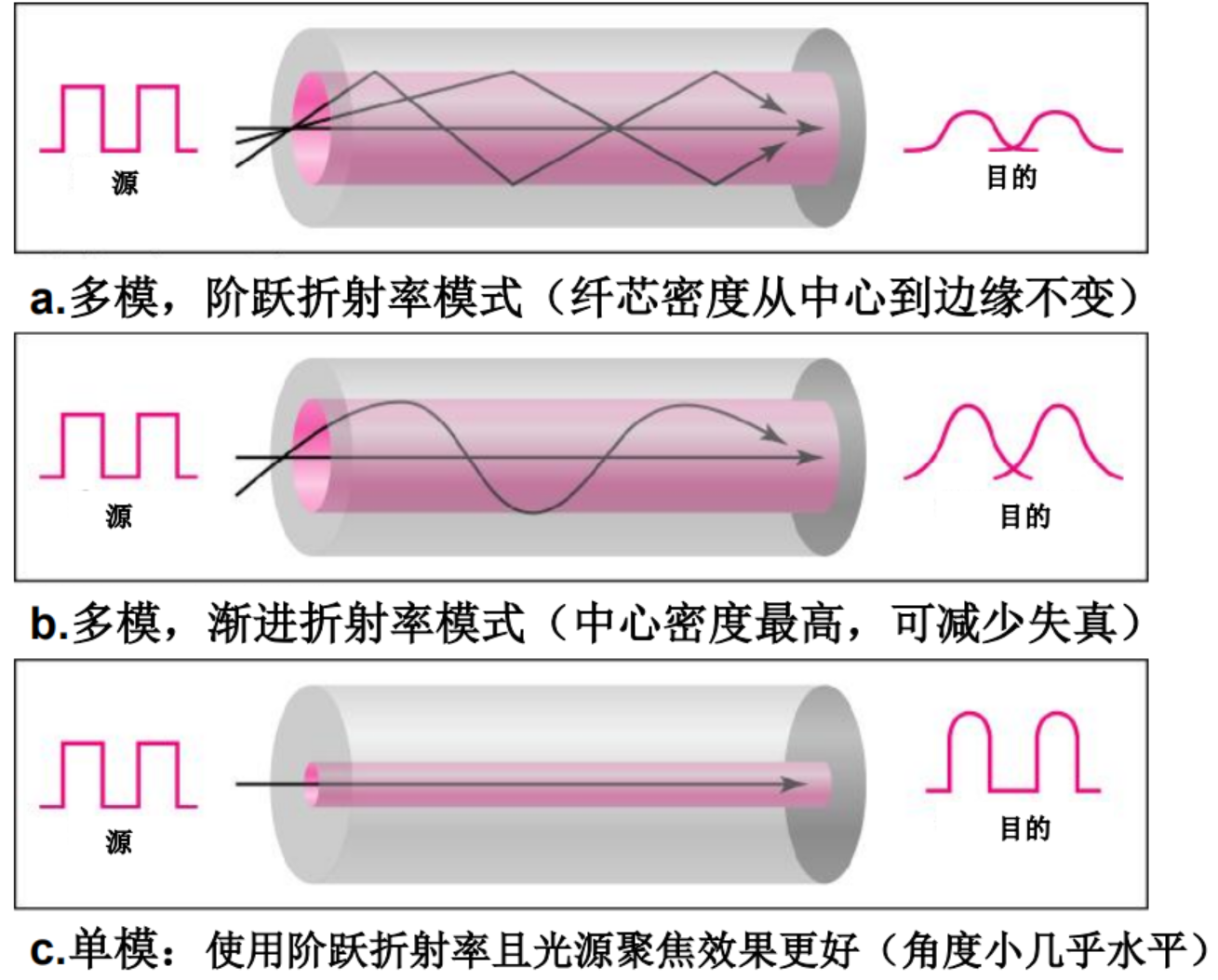
光纤电缆
传播模式:
- 多模, 阶跃折射率模式 (目的:传输数字信号)
- 多模,渐进折射率模式(目的:传输模拟信号)
- 单模, 使用阶跃折射率且光源聚焦效果更好