成帧
面向字符协议中的帧
- 数据用来自诸如ASCII编码系统的8位字符传输;
- 头部通常携带源端地址和目的端地址以及其他控制信息,而尾 部携带检错或纠错冗余位,也是8位的倍数;
- 为了将帧分离开来,在帧的开始和结束增加了8位(1字节)的标记(flag),标记由与协议相关的特殊字符组合而成,标明一个帧的开始和结束

字节填充和移除
字节填充是指如果存在与标记相同模式的字符,便在帧的数据部分填入一个特殊的字节(换义字符,ESC);当接收方遇到换义字符时,便会将它从数据段移走,并仍将下一字符作为数据
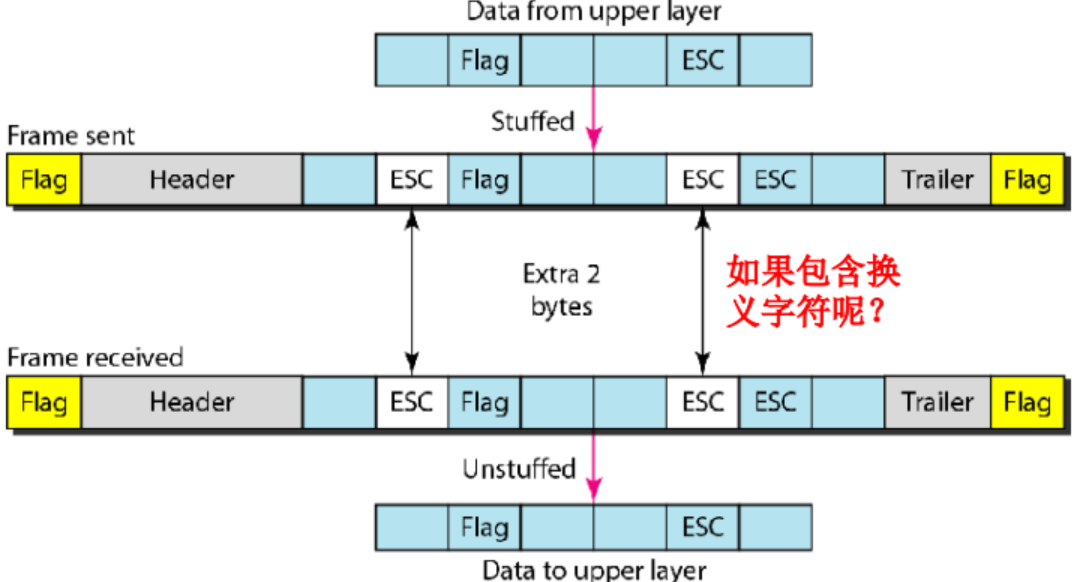
存在的问题: 广泛应用的编码系统,例如Unicode有16位和32位字符,与8位字符产生冲突,所以面向位协议将是大势所趋
面向位(比特)协议的帧
除了头部(也可能是尾部)之外,仍然需要一个分隔符将帧与帧区分开来,多数协议使用一个特殊的8位模式标记01111110作为分隔符来标明帧的开始和结束

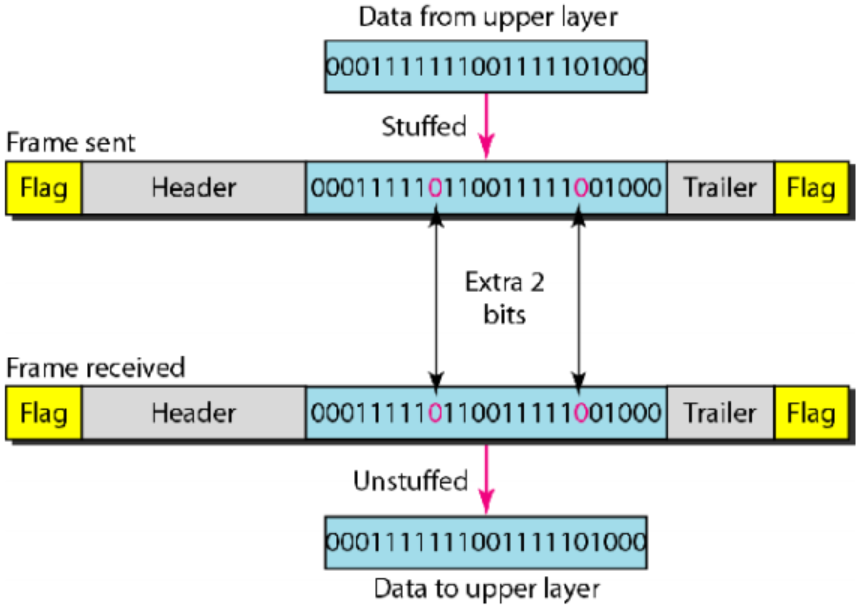
位填充是指在遇到1个0后面紧跟着5 个1时便添加一个0的过程,从而接收方不会误认为 0111110是一个标记。
位填充和移除过程
流量控制和差错控制
Q:数据链路层的流量控制和差错控制与传输层的控制有什么区别?
流量控制就是一系列程序,用来限制发送方在 等到确认之前发送的数据数量。
数据链路层的差错控制(通常指差错检测和重传的方法)基于自动重复请求ARQ(automatic repeat request),即重传数据。
协议
无噪声通道
不用使用差错控制,包括两种协议:不使用流量控制和使用流量控制。
停止等待协议(停止等待流量控制协议)
停止等待协议(stop-and-wait protocol):发送方发出一个帧后必须停下来,直到接收到来自接收方的确认(可以继续了),然后再发送下一个帧
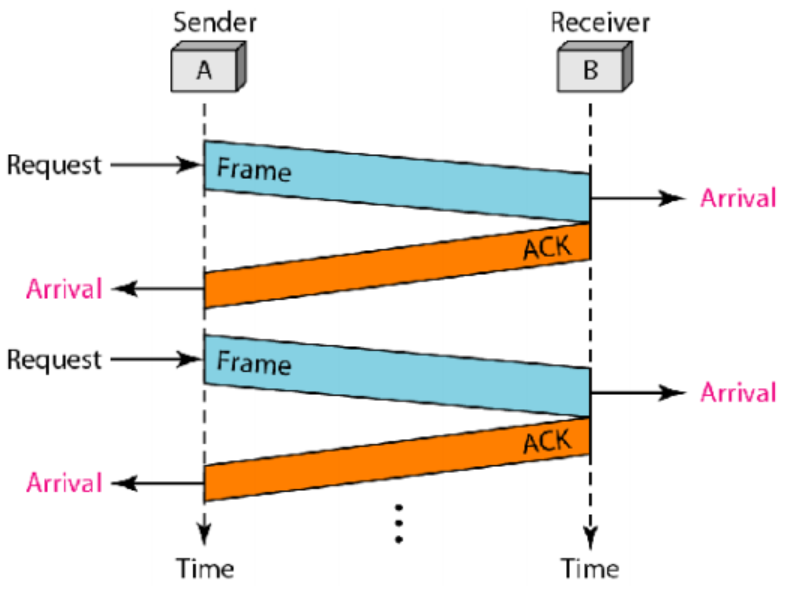
性能分析:
假设以帧序列$F_1,F_2,…,F_n$的形式发送一个较长的报文,则发送这些数据的总时间$T=nT_F$,而$T_F$是从$S_1$发送一个帧到$S_2$并接收到确认所需要的时间,有:
\[T_F = t_{prop} + t_{frame} + t_{proc} + t_{prop} + t_{ack} + t_{proc}\]其中:
- $t_{prop}$:从S1到S2的传播时间
- $t_{frame}$:传输一个帧所需要的时间
- $t_{proc}$:每个站的处理时间
- $t_{ack}$:传输一个确认需要的时间
假设处理时间相对来讲可忽略不计,且与数据帧相比, 确认帧显得非常短小可以忽略不计,则:
\[T = n \times (2t_{prop} + t_{frame})\]而真正用于传输数据的时间是$n \times t_{frame}$ ,其余均属于额外开销,所以该线路的利用率或有效率为:
\[U = \frac{n \times t_{frame}}{n (2t_{prop} + t_{frame})} = \frac{t_{frame}}{2t_{prop} + t_{frame}}\]定义参数$a = \frac{t_{prop}}{t_{frame}}$, 则:
\[U = \frac{1}{1 + 2a}\]如果$t_{prop}$和$t_{frame}$都是常数, 则a也是常数
V是介质的传播速度, d是线路的距离, R是传输速率, L是帧长度
a代表了用比特表示的媒体长度[R * (d/V)]与帧长度(L)的比值:
\[a = \frac{传播时间}{传输时间}= \frac{\frac{d}{V}}{\frac{L}{R}} = \frac{R D}{V L}\]例子:
在具有270ms时延的1Mbps卫星信道上使用1000比特的帧,停止等待协议的最大利用率是多少?
解:
\[U = \frac{1}{1+2a}\]其中
\[a = \frac{RD}{VL}\]由题意:
\[\frac{D}{V} = 270ms \quad R = 1Mbps \quad L = 1000bit\]所以:
\[a = \frac{10^6}{10^3} \times 270 \times 10^{-3} = 270\] \[U = \frac{1}{1+2a} = 0.185\%\]滑动窗口协议(滑动窗口流量控制协议)
对于滑动窗口流量控制,线路的利用率取决于窗口大小W以及a的值;
a为传播时间与传输时间的比值, 将帧传输时间归一化为1, 则传播时间即为a。
这样,第一帧在a+1时刻被接收方完全接受, 发送方传输出2a+1帧后, 完全接受确认帧。
(a)W>=2a+1:在A的窗口还没有用尽之前,帧1的确认已到 达,因此A能够连续不断的传送,则利用率为?
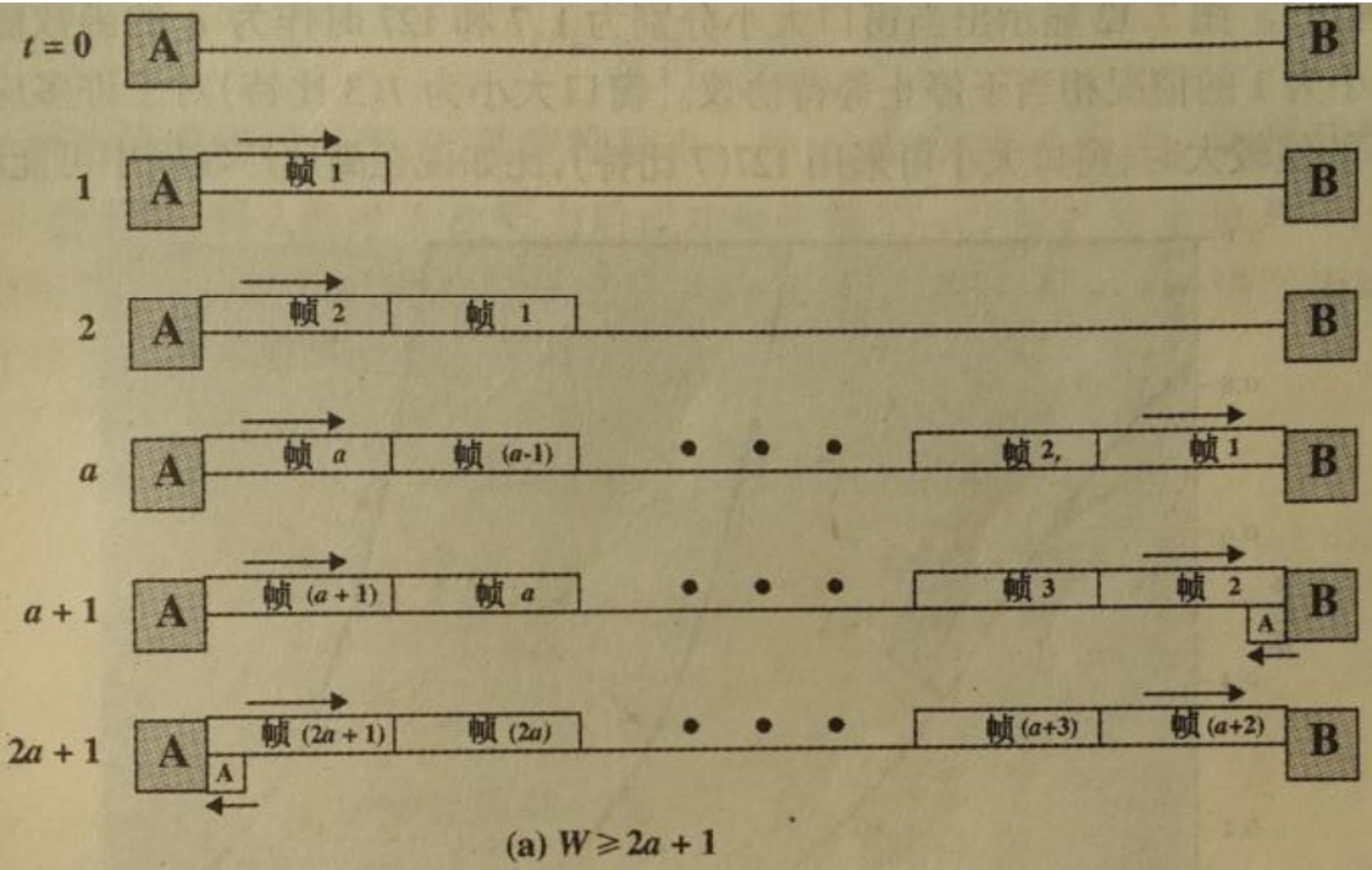
(b)W<2a+1:在t=W时刻A的窗口尽数用完,且无法发送其 他的帧,直到t=2a+1时刻,因此,线路的利用率是(2a+1)时 间单位内的W个时间单位,利用率为?
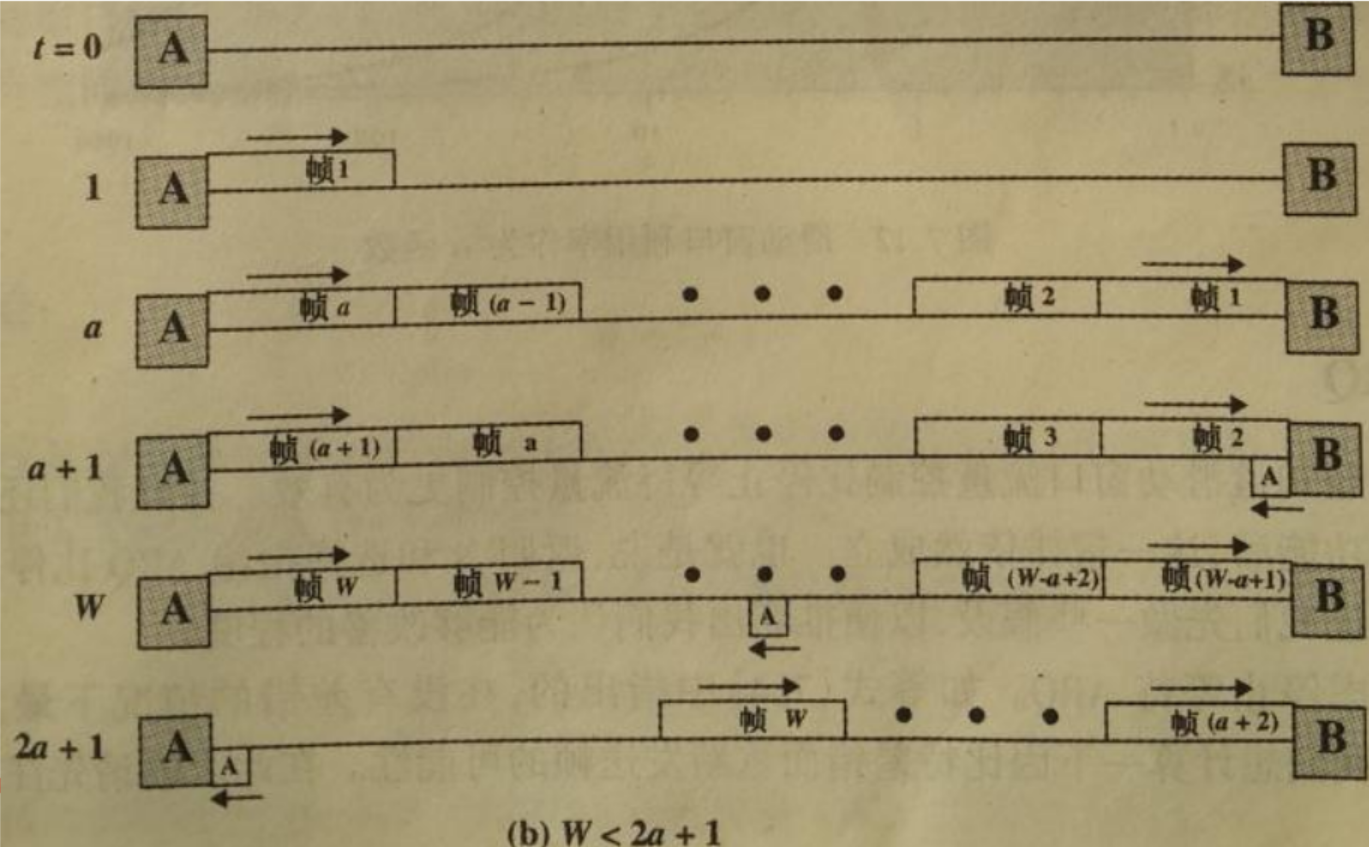
线路利用率如下所示:
\[U = \begin{cases} 1 & (W \geq 2a +1) \\ \frac{W}{2a + 1} & (W \leq 2a + 1) \end{cases}\]例子:
在具有270ms时延的1Mbps卫星信道上使用1000比特 的帧,若使用窗口大小为127的滑动窗口流量控制机制, 则线路的最大利用率是多少?
解:
\[a = \frac{D}{V} \frac{R}{L} = 270 \times 10^{-3} \times \frac{10^6}{10^3} = 270\] \[127 \leq 2a + 1\]所以:
\[U = \frac{W}{2a + 1} = \frac{127}{2 \times 270 + 1} = 23.5\%\]有噪声通道
停止等待ARQ(Stop-and-Wait Automatic Repeat Request)
在停止等待ARQ协议中,差错的检测由保留 已发送帧的副本并当重传定时器到时重传这个帧来实现。
停止等待ARQ使用序列号为每一个帧编号, 序列号基于模2运算。
- 确认号总是告知接收方期待的下一个帧的序列号;
- p如果帧0安全到达,接收方发送一个带有确认1的 ACK帧(表示下一个期待收到的是帧1),如果帧1安全到达,接收方则发送一个带有确认0的ACK帧 (表示下一个期待收到的是帧0)
在停止等待ARQ中,确认号总是以模2运算宣布期待收到的下一个帧的编号。
停止等待ARQ协议设计(发送方3个事件,接收方1个)
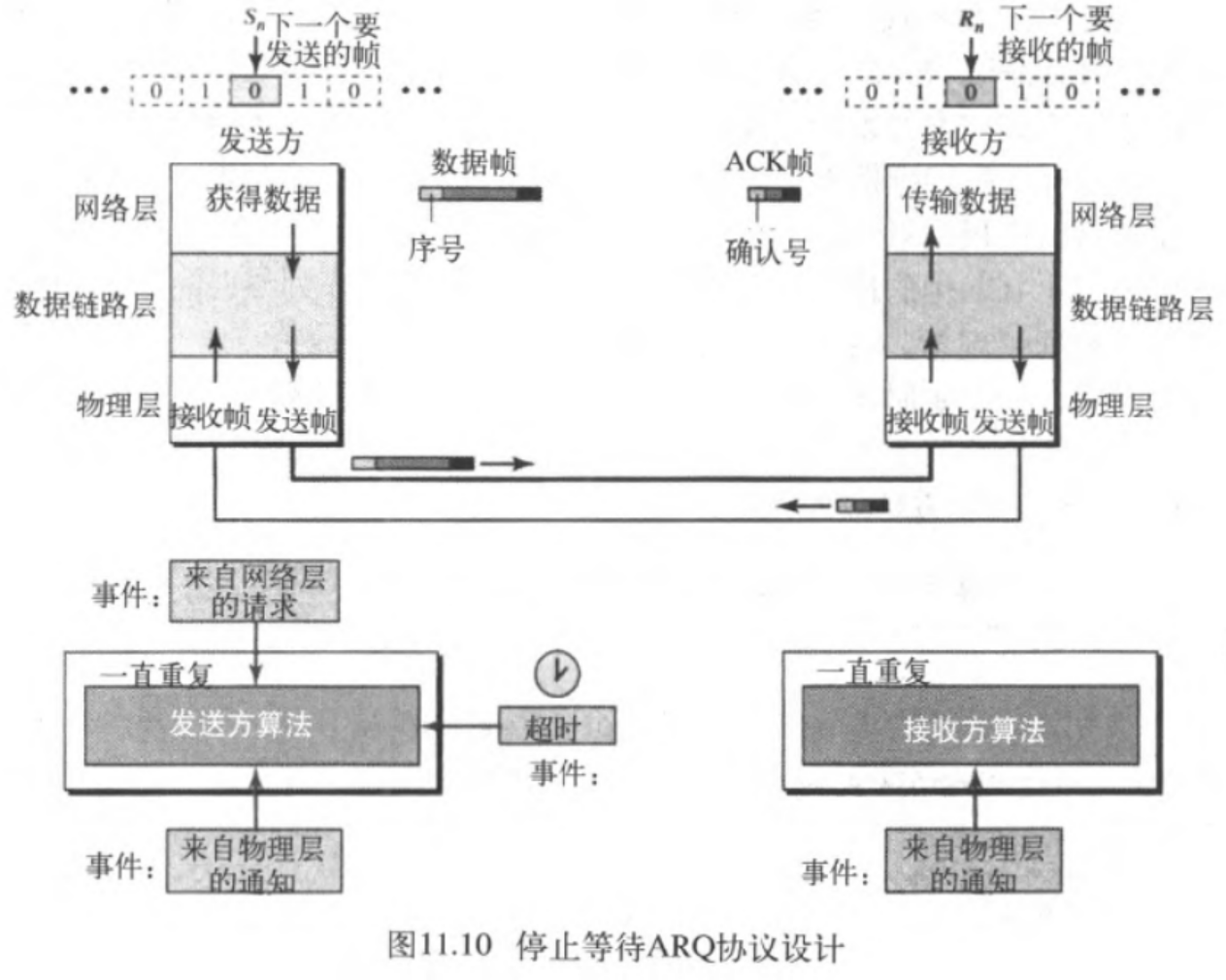
例子:
假定停止等待ARQ系统,带宽1Mbps,一个位往返一 次是20ms,求带宽时延乘积?如果帧长度是1000比特 ,链路利用率是多少?
解:
\[时延带宽积 = 时延 \times 带宽 = 20 \times 10^{-3} \times 10^6 = 20000bits\] \[链路利用率 = \frac{1000}{20000} = 5\%\]如果我们拥有一种协议能在停止和担 心确认之前发送15个帧,那么链路层的利用率是多少?
解:
带宽延迟乘积仍然是20000位。在一个往返过程中,系统能发送15个帧或者15000位,这意味着利用率是 15000/20000,即75%。当然,如果存在损坏的帧,那么利用率就要低很多,因为这些帧要被重发。
回退N帧ARQ(Go-Back-N Automatic Repeat Request)
在回退N帧ARQ协议中,在接收到确认之前能发送几个(或多个)帧,在确认到达之前会保存这些帧的几个(或多个)帧,在确认到达之前会保存这些帧的副本。
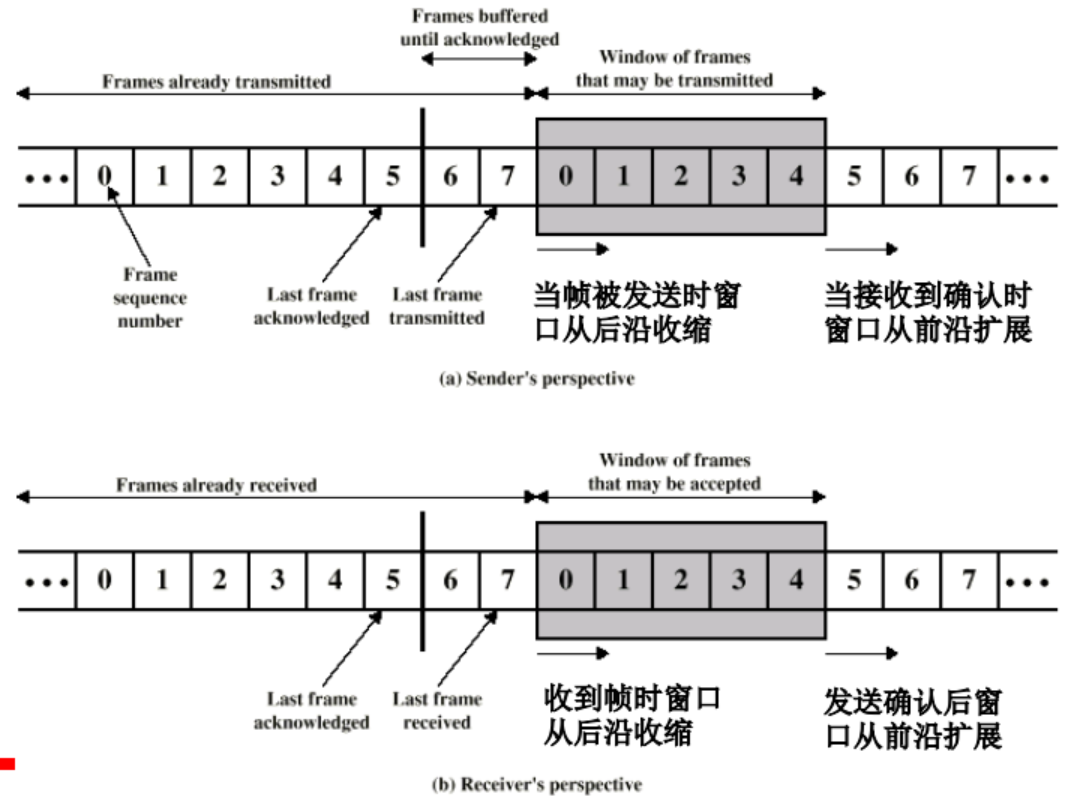
滑动窗口
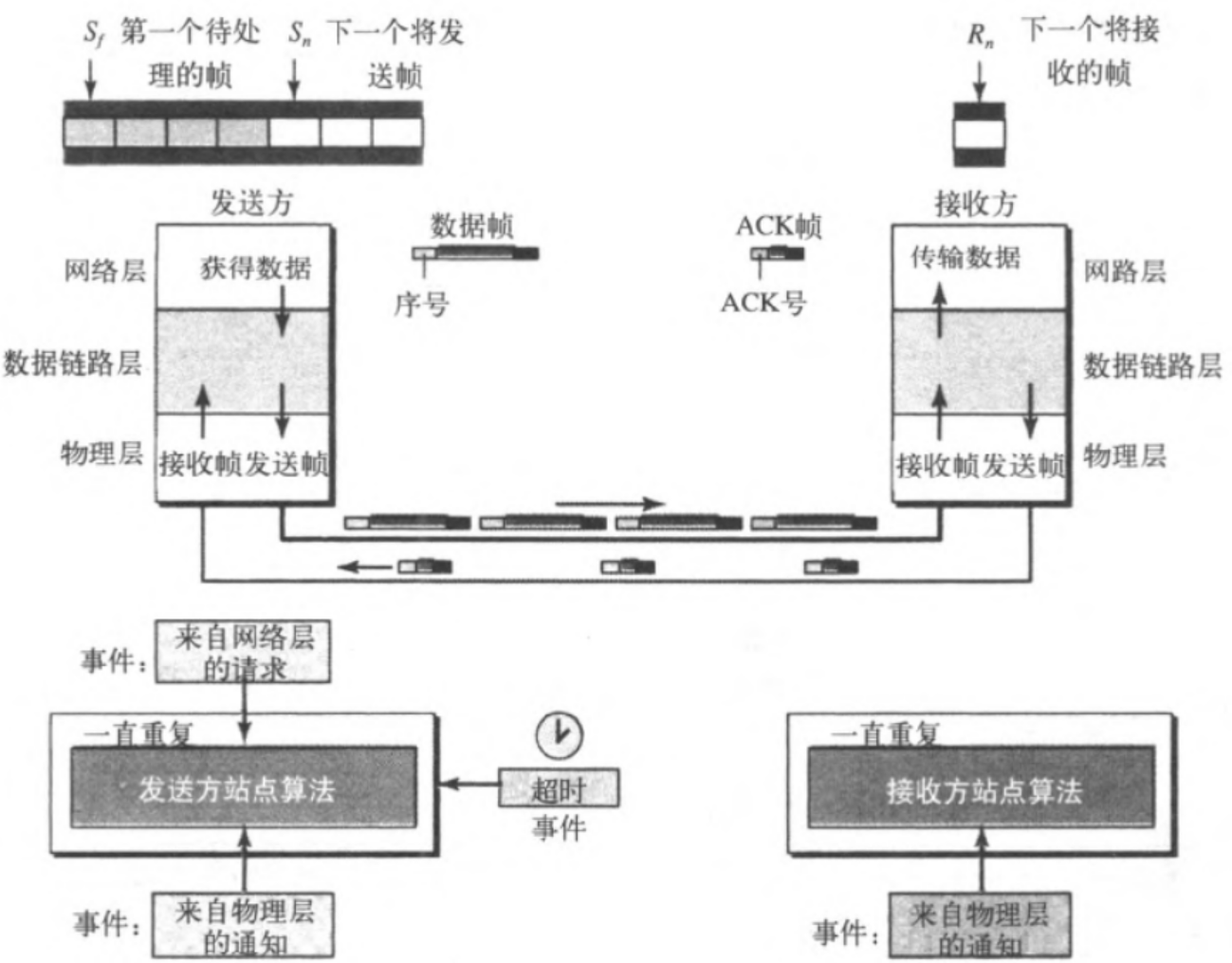
发送窗口是一个抽象概念,通过三个变量$S_f$(第一个待处理的帧)、$S_n$(下一个要发送的帧)和 S(窗口大小)定义的一个大小的帧)和 $S_{size}$(窗口大小)定义的一个大小 为2m−1(最大尺度)的假想盒子。
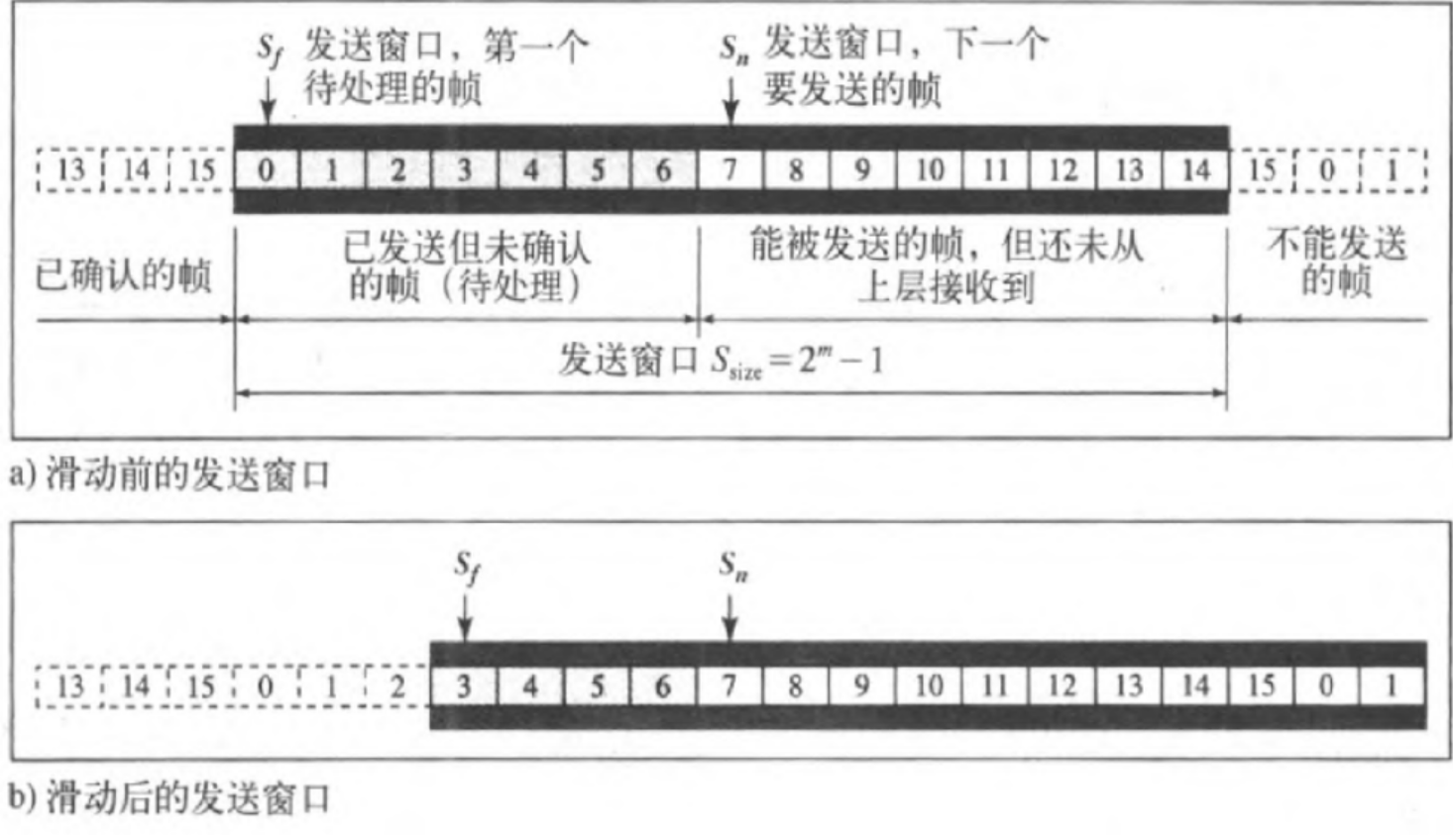
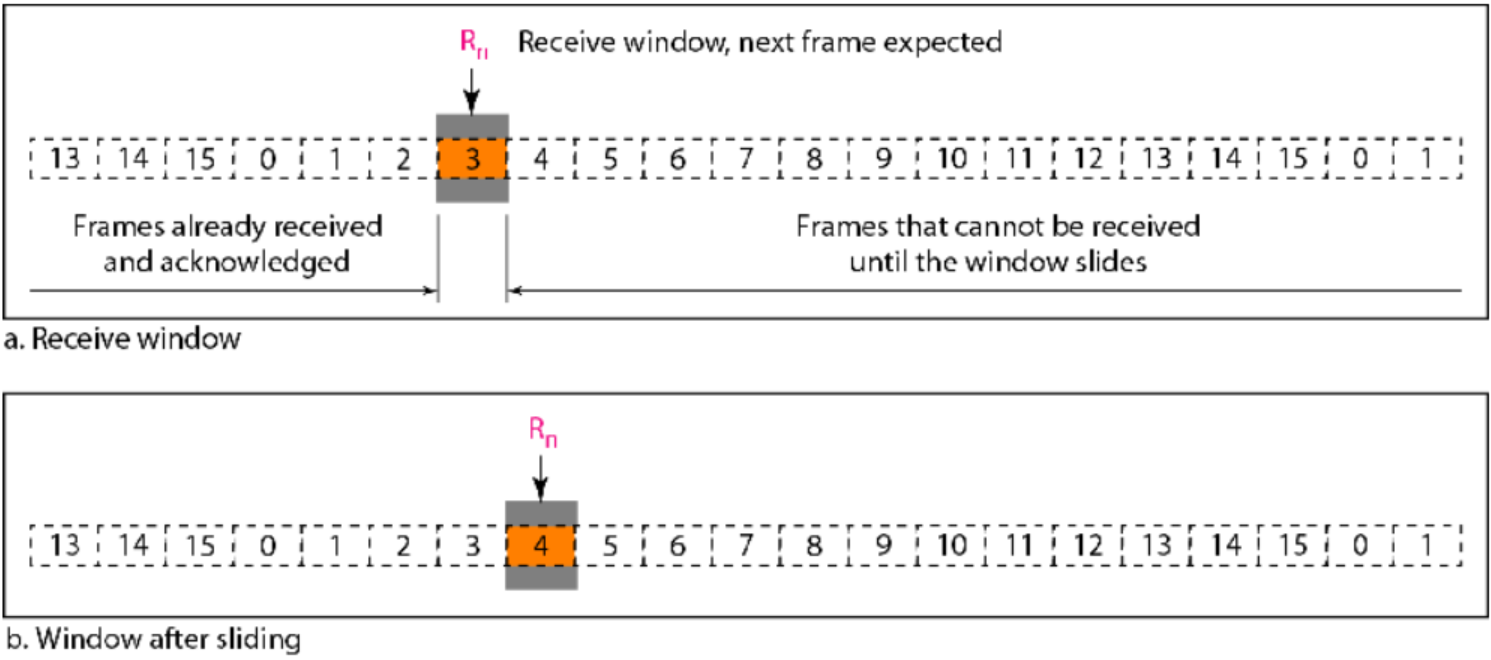
接收窗口是一个抽象概念,用变量Rn定义了一个 大小为1的接收窗口。当一个正确的帧到达时,窗 11.59大小为1的接收窗口。当一个正确的帧到达时,窗口滑动,但每次只滑动一个时隙。
定时器:只使用一个发送定时器,当第一个待处理的定时器到时时,发送所有的待处理帧;
确认:当一个帧安全有序到达,接收方发送一个确认;如果一个帧损坏了或者失序了,接收方便不响应并将丢弃所有后来的帧直到它收到一个所期待的帧(不响应使得不被确认的帧的定时器在发送方站点超时,这样会使发送方返回,并从定时器超时的那个帧开始重发所有的帧);接收方能为多个帧发送一个累积的确认;
重发帧:当定时器到时的时候,发送方会重发所有 待处理的帧,有可能回退N帧(名称的由来)。
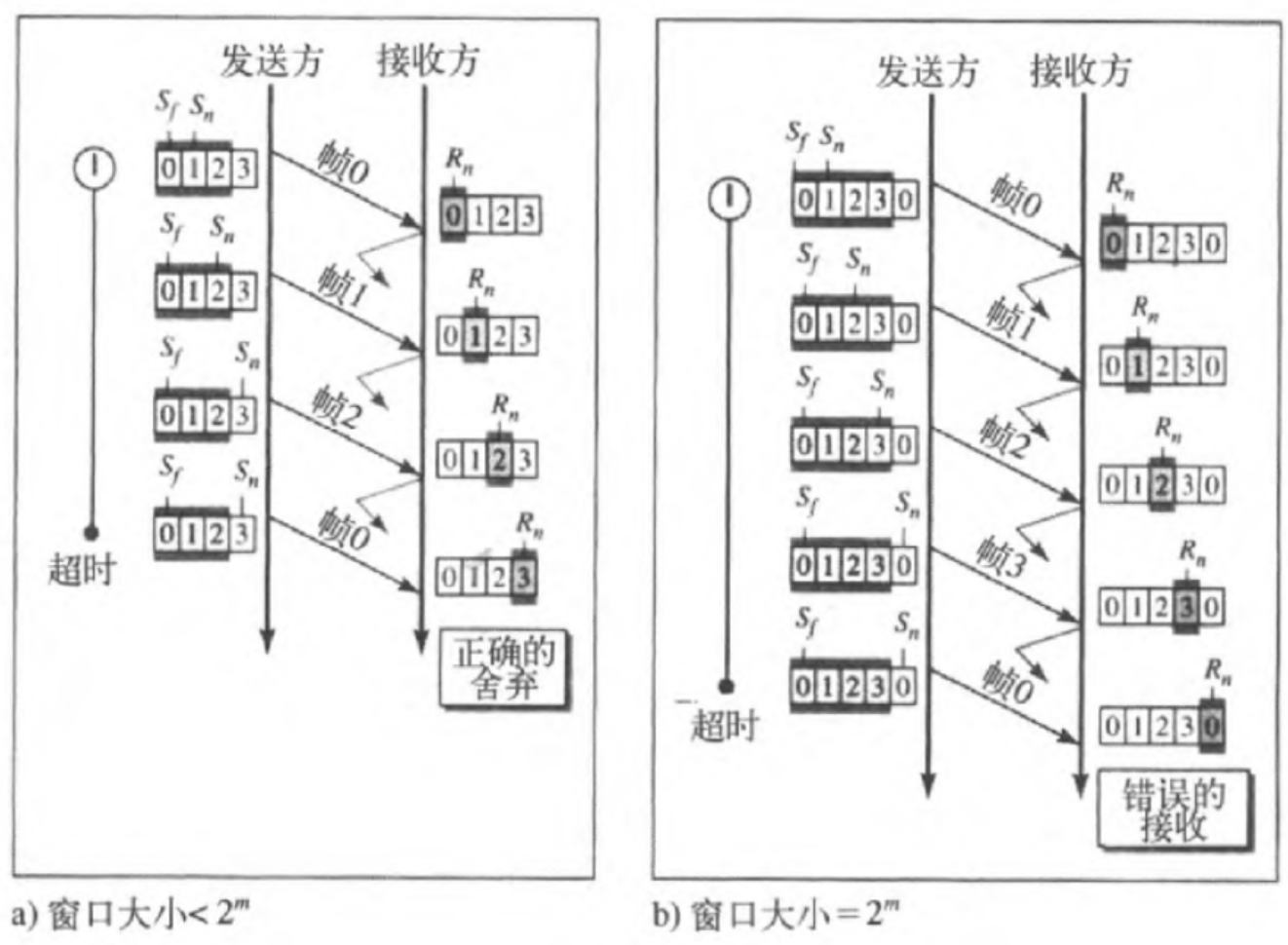
接收方只接受自己想要的那一帧, 发送方收到某一帧的ACK后就认为这之前的帧接收方全部收到了。
箭头转弯表示帧丢失
对左边的图来讲, ACK全部丢失,超时后发送方重发0帧,接收方舍弃。
对右边的图来讲,ACK全部丢失, 超时后发送方重发0帧,接收方正好要0帧,是错误的接收。
停止等待ARQ是发送窗口大小为1的回退N帧ARQ协议。
例子:
两个相邻的节点A、B采用滑动窗口协议,其序号占 用3比特,在回退N帧ARQ的方式中,发送方的窗口尺寸为5。假定A给B发送数据,对于下列事件,画出发送方窗口的位置,并说明可以继续发送的帧号。
(1)在A发送数据帧之前; (2)在A发送数据帧0,1,2之后,B应答了0,1帧,并且A收到了这些应答帧; (3)在A发送数据帧3,4,5之后,B应答了4号帧,并且A收到了这些应答帧。
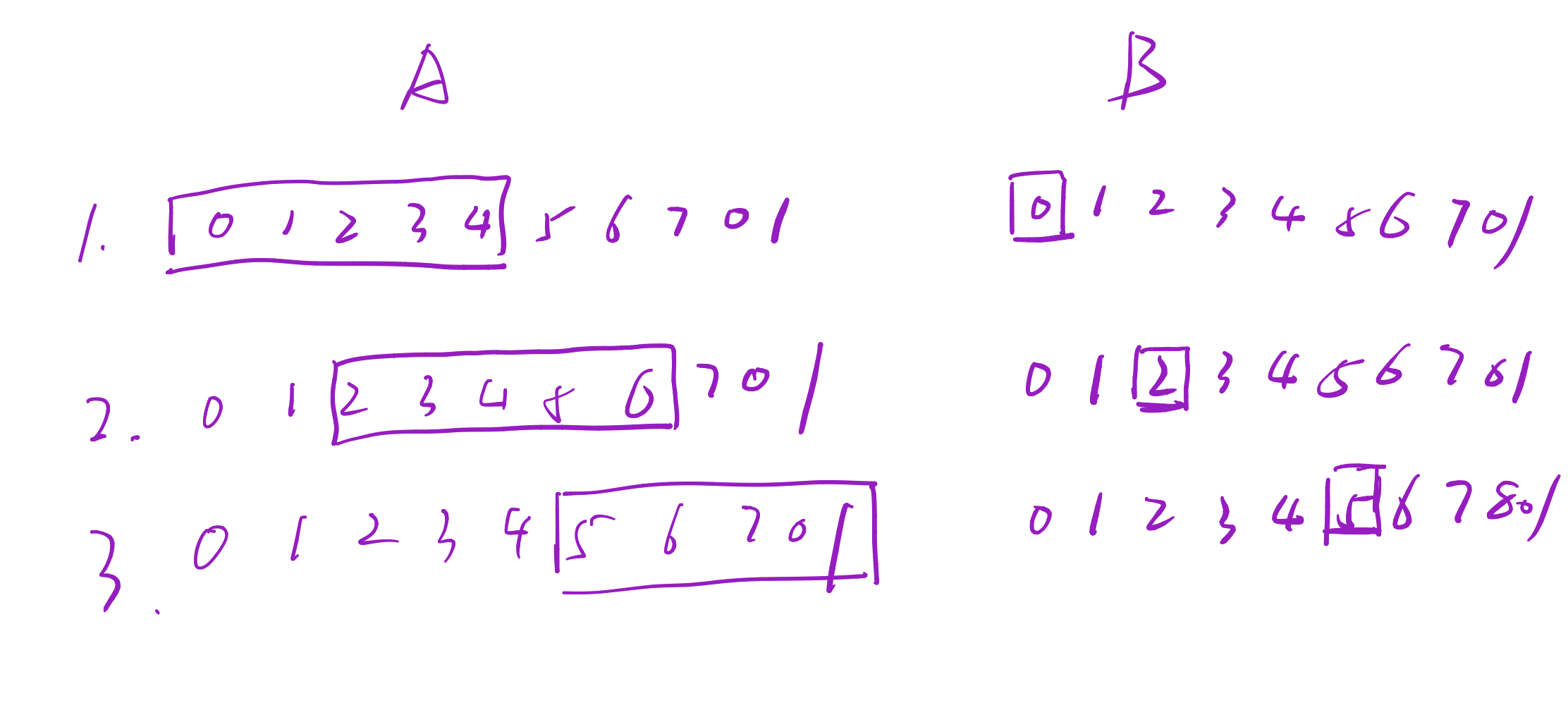
选择性重复 ARQ ( Selective Repeat Automatic Repeat Request)
发送窗口最大为$2^{m-1}$
接收窗口大小与发送窗口一样,最大也是$2^{m-1}$
允许与接收窗口大小一样多的帧乱序到达,并被保留直到有一 组有序帧能交付给网络层;
因为发送窗口的大小和接收窗口的一样,所有被发送的帧能乱序到达并被保存直到它们被传输;
需要指出的是接收方从不会将无序的数据分组交付给网络层
#