西电历年上机题目
2008年机试
Problems A
请写一个程序,判断给定整数序列能否构成一个等差数列?
每组数据由两行构成,第一行只有一个整数n(<100),表示序列长度(该序列中整数的个数),第二行为n个整数,每个整数的取值区间都为[-32768~32767],整数之间以空格或跳格间隔。
思路:
先用前两个最小的数算出公差,然后每次找最小的数,计算与前面的数的差是否等于公差。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class SolutionA{
public:
bool if_arithmetic_progression(vector<int> A){
if(A.size()==0) return 0;
if(A.size()<=2) return 1;
int pre, cur, min;
pre = find_min(A);
cur = find_min(A);
int error = cur - pre;
for(int i=0; i<A.size(); ++i){
pre = cur;
cur = find_min(A);
if(error == cur - pre) continue;
return 0;
}
return 1;
}
int find_min(vector<int> &A){
int min = A[0];
int loc = 0;
for(int i=1; i<A.size(); ++i){
if(A[i]<min){
min = A[i];
loc = i;
}
}
A.erase(A.begin()+loc, A.begin()+loc+1);
return min;
}
};
Problems B
判定给定正整数是不是“水仙花数”。“水仙花数”是指一个三位数,其各位数字的立方和等于该数, 例如153 = 1^3 + 5^3 + 3^3
输入说明:有多组数组,每组数据为一个正整数n(0<n<65536,占一行),为0时表示输入结束。
输入说明:对于每一组数据, 输入一个yes或no(表示该数是否为“水仙花数”)
思路:
将各位求出来, 然后求立方和是否等于原数。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class SolutionB{
public:
bool if_daffodils_number(int n){
int hundreds, tens, bits;
hundreds = n / 100;
tens = (n % 100) / 10;
bits = n % 10;
if(n==(cube(hundreds) + cube(tens) + cube(bits))) return 1;
return 0;
}
int cube(int n){
return n*n*n;
}
};
Problems C
Arnold变换是一种常见的图像置乱技术, Arnold变换的定义如下: 对于任意N*N矩阵(所有元素都相同的矩阵除外), 设i, j为矩阵元素原始下标,经过Arnold变换后新下标为i’, j’, 其满足下式: i’ = (i + j) mod N j’ = (i + 2j) mod N i, j: 0, 1, 2 … N-1 Arnold变换具有周期性, 即经过若干次变换后,矩阵回到最初状态, 且周期T与N的大小有关。 对于任意N>2, TN<=N^2/2, 编写程序输出给定的N(2<N<=10)对应的周期TN。
输入说明:对输入的每一个N,给出N*N矩阵的Arnold变换的周期T。
思路:
按照定义进行变换即可,注意变换的时候不要在原矩阵上变换,应该创建副本存储变换后的矩阵。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
class SolutionC{
public:
int Arnold_transform_T(vector<vector<int> > matrix){
int T = 1;
printMatrix(matrix);
vector<vector<int> > M1 = matrix, M2 = Arnold_transform(matrix);
printMatrix(M2);
while(!if_matrix_same(M1, M2)){
++T;
M2 = Arnold_transform(M2);
printMatrix(M2);
}
return T;
}
vector<vector<int> > Arnold_transform(vector<vector<int> > matrix){
// 这里定义出一个副本存储变换后的矩阵,注意不要在原矩阵上变换
vector<vector<int> > M = CreateMatrix(matrix.size());
for(int i=0; i<matrix.size(); ++i){
for(int j=0; j<matrix.size(); ++j){
int ii = (i + j) % matrix.size();
int jj = (i + 2 * j) % matrix.size();
M[i][j] = matrix[ii][jj];
}
}
return M;
}
bool if_matrix_same(vector<vector<int> > M1, vector<vector<int> > M2){
for(int i=0; i<M1.size(); ++i){
for(int j=0; j<M1.size(); ++j){
if(M1[i][j]!=M2[i][j]) return 0;
}
}
return 1;
}
vector<vector<int> > CreateMatrix(int n){
vector<vector<int> > M;
int c = 1;
for(int i=0; i<n; ++i){
vector<int> N;
for(int j=0; j<n; ++j){
N.push_back(c);
c++;
}
M.push_back(N);
}
return M;
}
void printMatrix(vector<vector<int> > M){
for(int i=0; i<M.size(); ++i){
for(int j=0; j<M.size(); ++j){
cout << M[i][j] << ' ';
}
cout << endl;
}
cout << endl;
}
};
Problems D
对于一个正整数n,如果它的各位之和等于它的所有质因数的各位之和, 则该数被称为smith数。 例如: 31527 = 3 * 3 * 23 * 151, 31527的各位之和为3+1+2+5+7=18, 它的所有质因数各位之和3+3+2+3+1+5+1=18, 因此,31527是一个smith数。 编写一个程序判断输入的正整数是不是smith数。
输入说明:有多组数据, 每组数据只有一个整数n(<10000, 占一行), 为0时表示输入结束。
输出说明:对于每一组数据,输出一个yes或no
思路:
两个判断条件
- 是不是质数
- 是不是因数
一开始想的是从小往大进行遍历,但是这样会有一个问题,质因数可能会有重复的,比如31527有两个质因数3。
因此改变思路,从大往小找质因数,每次找到一个质因数,除以质因数后,再重新求新得到的数的质因数,这样不会有质因数的丢失。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
class SolutionD{
public:
bool is_smith(int n){
vector<int> factor;
int n_backup = n;
while(n!=1){
int i = 2;
while(i<=n){
if((is_prime_number(i))&&is_factor(n, i)){
factor.push_back(i);
// 如果直接遍历,重复的质因数会丢失
// 每次除质因数后的结果,再去找质因数
n = n / i;
break;
}
++i;
}
}
int sum_factor = 0;
for(int i=0; i<factor.size();++i){
cout << "factor " << i << ": " << factor[i] << endl;
sum_factor += bits_sum(factor[i]);
};
cout << "sum_factor: " << sum_factor << endl;
cout << "n_sum: " << bits_sum(n_backup) << endl;
if(bits_sum(n_backup)==sum_factor) return 1;
else return 0;
}
bool is_prime_number(int n){
int c = 2;
while(n%c!=0){
c++;
}
if(c!=n) return 0;
else return 1;
}
bool is_factor(int n, int factor){
if(n%factor == 0) return 1;
return 0;
}
int bits_sum(int n){
int bits, tens, hundreds, thousands, ten_thousand;
ten_thousand = n / 10000;
thousands = (n % 10000) / 1000;
hundreds = (n % 1000) / 100;
tens = (n % 100) / 10;
bits = n % 10;
return ten_thousand + thousands + hundreds + tens + bits;
}
};
Problems E
请写一个程序, 计算R^n精确结果(0.0<R<99.999, n是整数且0<n<=25)
输入说明:有多组数据,每组数据占一行,用一对数据表示, 第一个数据是R (含小数点6位), 第二个数据是n, 两个数据之间有一个空格。
输入说明: 对每个 输入 输出其结果(占一行)
思路:
这题我是没思路的,想到用数组存储,但是感觉又太麻烦没有继续。
看了学长讲解后,有了部分思路,对于整数类型的输入,可以求解。
用字符串存储各位,一位一位地去计算,将个位保留在本数组,然后再处理进位问题即可。
对于浮点数的输入无法计算,因为计算机是二进制存储的,例如当输入12.123时,它的结果其实是12.1299999…,没有好的方法去处理它,放弃。
如果按学长那样直接输入的就是字符串的话,会好处理很多。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
class SolutionE{
public:
vector<int> cal_pow(vector<int> R, int n, int x){
int temp = 0;
vector<int> t;
while(--n){
temp = 0;
for(int i=R.size()-1; i>=0; --i){
temp += R[i] * x;
t.insert(t.begin(), temp%10);
temp /= 10;
}
while(temp!=0){
t.insert(t.begin(), temp%10);
temp /= 10;
}
R = t;
t.erase(t.begin(), t.end());
}
return R;
}
vector<int> int2vec(int n){
vector<int> t;
while(n!=0){
t.insert(t.begin(), n%10);
n /= 10;
}
return t;
}
vector<int> float2vec(ld f){
ld temp = f - (ld)(int)f;
vector<int> t;
while(temp==0){
temp *= 10;
t.push_back(int(temp));
temp = temp - (ld)int(temp);
}
return t;
}
};
2009年机试
Problems A
请写一个程序, 给出指定整数范围[a, b]内所有的完数,一个数如果恰好等于除它本身以外的所有因子之和,这个数就称为完数,例如6是完数,因为6=1+2+3.
输入说明:共一组数据为两个正整数,分别表示a和b(1<a<b<10^5).
输出说明:指定范围内的所有完数, 每个数占一行。
思路:
- 在范围内遍历
- 计算数的所有因子
- 判断是否是完数
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class SolutionA{
public:
vector<int> find_all_perfect_numbers(int a, int b){
vector<int> perfect_numbers;
int c = a;
while(c!=b){
if(if_perfect_number(c)) perfect_numbers.push_back(c);
c++;
}
return perfect_numbers;
}
bool if_perfect_number(int n){
int factor_sum = 0;
vector<int> factors;
factors = find_factors(n);
for(int i=0; i<factors.size(); ++i){
factor_sum += factors[i];
}
if(factor_sum == n) return 1;
return 0;
}
vector<int> find_factors(int n){
int c=1;
vector<int> factors;
while(c!=n){
if(n%c==0) factors.push_back(c);
c++;
}
return factors;
}
};
Problems B
请写-一个程序,对于一个m行m列的(1<m<10)的方阵,求其每一行,每一列及主对角线元素之和,最后按照从大到小的顺序一次输出。
输入说明:共一组数据,输入的一行为一个正整数,表示m, 接下来的m行,每行m个整数表示方阵元素。
输出说明: 从大到小排列的一行整数,每个整数后跟一个空格,最后换行。
思路:
- 计算迹(对角线之和)
- 计算各行之和
- 计算各列之和
- 排序
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
class SolutionB{
public:
void sum_sort(vector<vector<int> > M){
int Trace = trace(M);
vector<int> Sum_row = sum_row(M);
vector<int> Sum_col = sum_col(M);
vector<int> sum;
sum.push_back(Trace);
for(int i=0; i<Sum_row.size(); ++i){
sum.push_back(Sum_row[i]);
}
for(int i=0; i<Sum_col.size(); ++i){
sum.push_back(Sum_col[i]);
}
sort(sum.begin(), sum.end());
for(int i=sum.size()-1; i>=0; --i){
cout << sum[i] << " ";
}
cout << endl;
}
vector<int> sum_row(vector<vector<int> > M){
int sum = 0;
vector<int> Sum_row;
for(int i=0; i<M.size(); ++i){
for(int j=0; j<M.size(); ++j){
sum += M[i][j];
}
Sum_row.push_back(sum);
sum = 0;
}
return Sum_row;
}
vector<int> sum_col(vector<vector<int> > M){
int sum = 0;
vector<int> Sum_col;
for(int i=0; i<M.size(); ++i){
for(int j=0; j<M.size(); ++j){
sum += M[j][i];
}
Sum_col.push_back(sum);
sum = 0;
}
return Sum_col;
}
int trace(vector<vector<int> > M){
int sum = 0;
for(int i=0; i<M.size(); ++i){
for(int j=0; j<M.size(); ++j){
if(i==j) sum += M[i][j];
}
}
return sum;
}
vector<vector<int> > CreateMatrix(int n){
vector<vector<int> > M;
vector<int> N;
srand(time(NULL));
for(int i=0; i<n; ++i){
for(int j=0; j<n; ++j){
N.push_back(rand()%10);
}
M.push_back(N);
N.erase(N.begin(), N.end());
}
return M;
}
void printMatrix(vector<vector<int> > M){
for(int i=0; i<M.size(); ++i){
for(int j=0; j<M.size(); ++j){
cout << M[i][j] << " ";
}
cout << endl;
}
}
};
Problems C
对于给定的字符序列,从左至右将所有的数字字符取出来拼接成个无符号整数(字符序列长度小于100,拼接出整数小于2^31),计算并输出该整数的一个最大因子(如果是素数,则其最大因子为自身)
输入说明:有多组数据,输入数据的第一行为一个正整数,表示字符序列的数目,每组数据为一行字符序列。
输出说明:对每个字符序列,取出所得整数的最大因子,若字符序列中没有数字或者找出的
输入: 3 sdf0ejg3.f?9f ?4afd0s&2d79*(g abcde
输出: 13 857 0
学长的题目输入给错了,在CSDN找到了正确的输入。
思路:
- 每次读入一行字符串
- 利用公式$n = 10 \times n + x$计算,这里n用来计数该哪一位了, x为本字符数字变成的所表示真实数字
- 遍历找最大因子
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class SolutionC{
public:
ll str2num(string str){
ll num = 0;
for(int i=0; i<str.size(); ++i){
if(str[i]>='0' && str[i] <='9'){
num = num * 10 + str[i] - '0';
}
}
cout << num << endl;
if(num == 0) return 0;
if(if_prime_number(num)) return num;
ll factor = num - 1;
while(1){
if(num%factor==0) return factor;
factor--;
}
return -1;
}
bool if_prime_number(ll num){
ll i = 2;
while(i!=num){
if(num%i == 0) return 0;
++i;
}
return 1;
}
};
这个题在牛客上时间超限了。。。就这样把,以后再优化。
Problems D
己知某二义树的先序序列和中序序列,编程计算并输出该二义树的后序序列。
入说明:仅一组数据,分为两行输入,第一行表示指定二叉树的先序序列, 第二行表示该 二义树的中序序列,序列元素均为大写英文字符,表示二义树的结点。
输出说明:第一行上输出该二又树的后序序列。
输入样本: ABDGCEFH DGBAECHF
输出样本: GDBEHFCA
思路:
这个题之前在牛客上做过,那次是做出来了的,这次却卡住了。
这次是想直接利用字符串将后序遍历打印出来。
事实上,还是利用前序和中序将二叉树先构造出来,再打印后序遍历,会容易一些。
细心地手动模拟一边应该就可以做得出来。
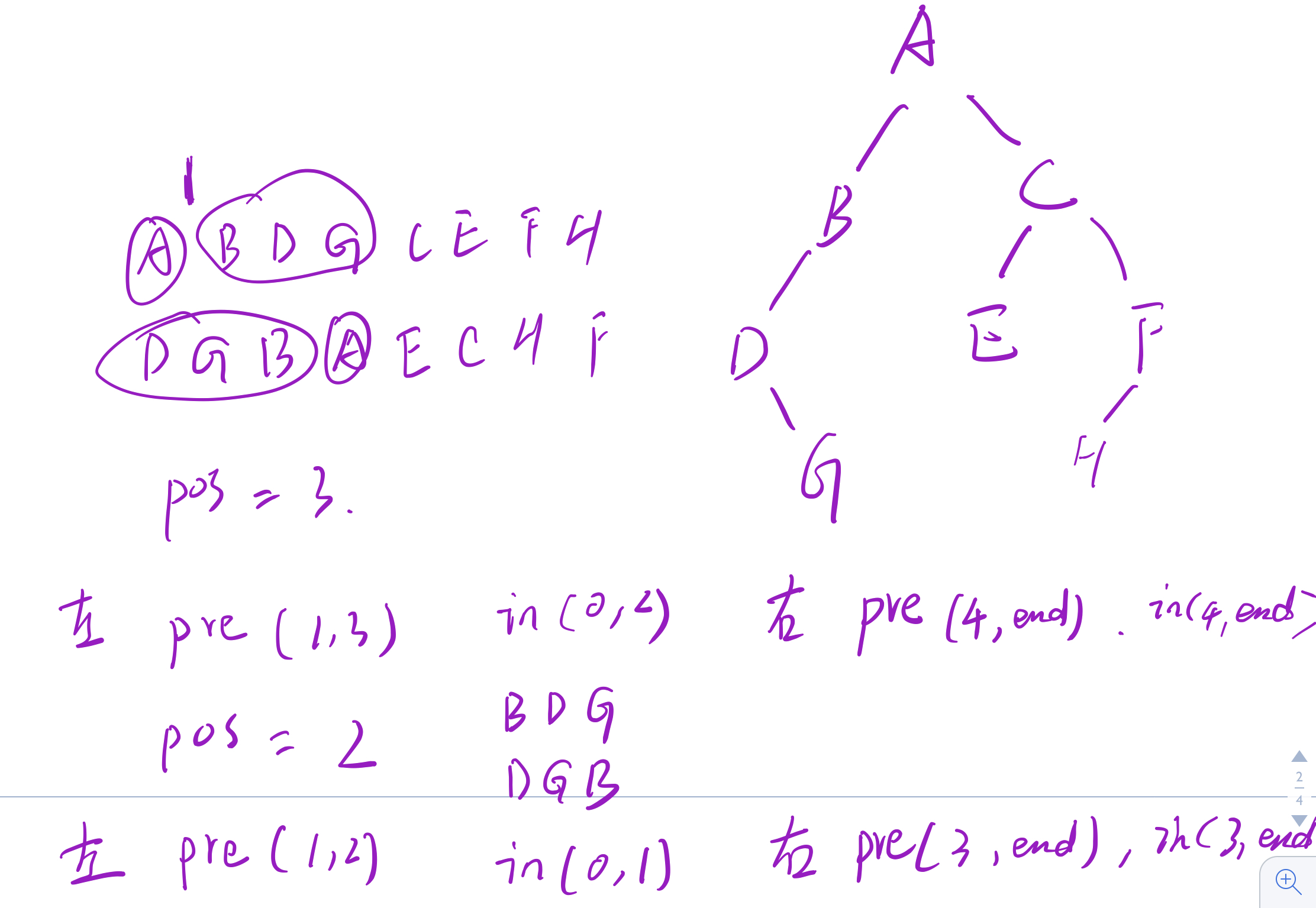
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
struct TreeNode{
char val;
TreeNode* left;
TreeNode* right;
TreeNode(ll x):
val(x), left(NULL), right(NULL){
}
};
// 本题的经验:vector的用法大部分都可以迁移到string上
class SolutionD{
public:
TreeNode* reconstruct_Tree(string preOrder, string inOrder){
if(preOrder.size()==0||inOrder.size()==0) return NULL;
TreeNode *p = (TreeNode*)malloc(sizeof(TreeNode));
p->val = preOrder[0];
char root = preOrder[0];
ll pos = inOrder.find(root);
if(preOrder.begin()+ pos + 1 < preOrder.begin()+1){
p->left = NULL;
}else{
p->left = reconstruct_Tree(string(preOrder.begin()+1, preOrder.begin()+pos+1),
string(inOrder.begin(), inOrder.begin()+pos));
}
if(preOrder.begin()+pos+1>preOrder.end()){
p->right = NULL;
}else{
p->right = reconstruct_Tree(string(preOrder.begin()+pos+1, preOrder.end()),
string(inOrder.begin()+pos+1, inOrder.end()));
}
return p;
}
void print_Tree_preOrder(TreeNode* T){
if(T==NULL) return;
cout << T->val << ' ';
print_Tree_preOrder(T->left);
print_Tree_preOrder(T->right);
}
void print_Tree_inOrder(TreeNode* T){
if(T==NULL) return;
print_Tree_inOrder(T->left);
cout << T->val << ' ';
print_Tree_inOrder(T->right);
}
void print_Tree_postOrder(TreeNode* T){
if(T==NULL) return;
print_Tree_postOrder(T->left);
print_Tree_postOrder(T->right);
cout << T->val << ' ';
}
};
Problems E
请写一个程序,判定给定表达式中的括号是否匹配, 表达式中的合法括号为 “(“, “)”, “[”, “]”, “{“, “}”, 这三个括号的按照任意顺序嵌套使用。
输入说明:有多个表达式,输入数据的第一行是表达式的数目,每个表达式占 一行。
输出说明:对每个表达式,若其中的括号是匹配的,则输出“yes”, 否则输出 “no”。
输入样本 4 [(d+f)*{}] [(2+3)] ()} [4(6]7)9
输出样本: yes yes no no
思路:
用一个栈来存储左括号,每当遇到一个右括号的时候,判断与栈顶的括号是否匹配
若不匹配,返回0。
若匹配, 栈顶出栈。
循环执行,最后看是否栈空
若栈空,返回1
若栈不空, 返回0
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
class SolutionE{
public:
bool Parentheses_Matching(string str){
stack<char> S;
for(int i=0; i<str.size(); ++i){
if(str[i]=='('||str[i]=='['||str[i]=='{') S.push(str[i]);
if(str[i]==')'||str[i]==']'||str[i]=='}'){
if(S.empty()) return 0;
if(str[i]==')'){
if(S.top()!='('){
return 0;
}else{
S.pop();
}
}
if(str[i]==']'){
if(S.top()!='['){
return 0;
}else{
S.pop();
}
}
if(str[i]=='}'){
if(S.top()!='{'){
return 0;
}else{
S.pop();
}
}
}
}
if(!S.empty()) return 0;
return 1;
}
};
2011年机试
Problems A
编写一个程序,从键盘输入n个非零整数(0<n<1000),将这n个数中每个数的各位数字取出来相加, 并按照从小到大的次序一次输出这些数字和。
例如,497的各位数字和为20(4+9+7),1069的各位数字和为16(1+0+6+9)
输入格式说明:输入整数之间以空格分隔,输入0时结束。
输出格式说明:在一行上从小到大输出计算结果,整数之间用1个空格分隔,最后换行。
输入示例:
497 1069 68 71 137 0
思路:
- 将输入的各数存入vector
- 求 vector中各数 各位数字取出来相加 存入一个vector
- sort排序
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class SolutionA{
public:
void sum_sort(vector<ll> numbers){
vector<ll> sums;
for(int i=0; i<numbers.size(); ++i){
sums.push_back(sum_bits(numbers[i]));
}
sort(sums.begin(), sums.end());
for(int i=0; i<numbers.size(); ++i){
cout << sums[i] << ' ';
}
}
ll sum_bits(ll n){
vector<ll> cache;
while(n!=0){
cache.push_back(n%10);
n /= 10;
}
ll sum = 0;
for(int i=0; i<cache.size(); ++i){
sum += cache[i];
}
return sum;
}
};
Problems B
写一个程序,找出给定矩阵的马鞍点, 若一个矩阵中的某元素在其所在行最小而在其所在列最大,则该元素为矩阵的一个马鞍点。
输入说明:输入数据由m+1行构成, 第一行只有两个整数m和n(0<m<100.0<n<100),分别表示矩阵的行数和列数, 接下来来的m行、每行n个整数表示矩阵元素(矩阵中的元素不同)。整数之间以空格间隔。
输出说明:在一行上输出马鞍点的行号、列号(行号和列号从0开始记数)及元素的值(用一个空格分隔),之后换行;若不存在马鞍点,则输出一个字符串”no”后换行。
输入示例:(注意:本题裁判机上输入数据的第一行整数不一定是4和3)
4 3
11 13 121
407 72 88
25 58 1
134 30 62 \
输出示例:
1 1 72
思路:
三重循环:
- 第一次循环找一行中最小的
- 第二次循环找该行中最小的, 看是否是同一个数
- 循环执行上面两个循环,遍历完所有行
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class SolutionB{
public:
void find_Saddle_point(vector<vector<ll> > M){
ll min = 0, max = 0;
ll row = 0, col = 0;
ll flag = 0;
for(int i=0; i<M.size(); ++i){
min = M[i][0];
col = 0;
for(int j=0; j<M[i].size(); ++j){
if(M[i][j]<min){
min = M[i][j];
col = j;
}
}
max = min;
for(int k=0; k<M.size(); ++k){
if(M[k][col]>max){
max = M[k][col];
row = k;
}
}
if(max == min){
cout << row << ' ' << col << ' ' << M[row][col] << endl;
flag = 1;
}
}
if(flag==0) cout << "no" << endl;
}
};
Problems C
有一种简单的字符串压缩算法,对于字符串中连续出现的同一个字符,用该字符串加上连续出现的次数来表示(连续出现次数小于3时不压缩),例如, 字符串aaabbbabaaaaaaaaabbb可压缩为a5b3aba13b4、请设计一个程序,将采用该压缩方法得到的字符串解压缩,还原出原字符串并输出。
输入格式说明:在一行上输入一个字符串。(长多不超过50)
出格式说明:在一行上输出解压缩后的字符串(长度不超过100),最后换行
输入示例:
a5b3aba13b4
输出示例:
aaaaabbbabaaaaaaaaaaaabbbb
思路:
- 定位到数字字符
- 将数字字符串转化为数字
- 删除数字部分的字符串
- 插入数字长度的字符
需要有指针pre指向数字前的一个字符,还需要两个指针定位数字字符串的长度
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class SolutionC{
public:
void unzip_str(string str){
ll pre = 0;
string str_num;
for(int i=1;i<str.size();++i){
// 要保证pre指针在i指针前面
pre = i-1;
if(str[i]>='0'&&str[i]<='9'){
ll j = i;
while(str[j]>='0'&&str[j]<='9'){
str_num.append(1, str[j]);
++j;
}
ll num = str2num(str_num);
cout << num << endl;
str.erase(str.begin()+i, str.begin()+j);
str.insert(i, num-1, str[pre]);
str_num.erase(str_num.begin(), str_num.end());
cout << str << endl;
i = i + num - 1;
pre = i;
}
}
cout << str << endl;
}
ll str2num(string str_num){
ll num = 0;
for(int i=0; i<str_num.size();++i){
num = 10 * num + (str_num[i] - '0');
}
return num;
}
};
注意这里str.erase()的用法是不对的,str.erase(pos, n)删除从pos开始的n个字符,结果正确可能碰巧。
Problems D
用于通信的电文由n(4<n<30)个字符组成, 字符在电文中出现的频度(权值)为w1,w2,,,,wn,试根据该权值序列构成哈大蔓树,并计算该树的带权路径长度。
输入说明:
仅一组数据,为两行输入:
第一行为n的值,第二行为n 个整数,表示字符出现的频度
输出说明:一个整数,表示所构造哈夫曼树的带权路径长度(输出整数后换行)。
思路:
构造一个数据结构Node,包含weight、lchild、rchild、parent,length。
用一个Node类型的vector Tree来存储哈夫曼树
构造哈夫曼树:
- vector Tree前n个位置存n个叶子节点
- 制造一个Tree的副本A,所有操作在A上进行,只有在添加节点时,才操作Tree
- 每次在A中找最权重最小的叶子节点,返回它的坐标, 将权重赋值为-1(标志它被用来构造过了)。 这样做是为了保证它和Tree的坐标相对应。
- 找到两个最小的节点,生成新节点,权重为两个节点权重之和,两节点parent指向新节点,新节点左右孩子分别指向两节点。
- 循环执行上述步骤,循环n-1次停止
计算带权路径长度:
构造好哈夫曼树后,从前到后计算各节点长度, 通过parent指针,直到根节点parent指针为-1,即可计算各节点长度,长度乘以权重即得到带权路径长度。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
struct Node{
ll weight;
ll lchild, rchild, parent, length;
};
class SolutionD{
public:
void Huffman_Tree_Structor(vector<Node> &Tree){
vector<Node> A = Tree;
Node T;
ll t = Tree.size();
for(int i=0; i<t-1; ++i){
ll min = find_min(A);
ll second_min = find_min(A);
T.weight = Tree[min].weight + Tree[second_min].weight;
T.parent = -1;
T.lchild = min;
T.rchild = second_min;
A.push_back(T);
Tree.push_back(T);
Tree[min].parent = Tree.size()-1;
Tree[second_min].parent = Tree.size()-1;
}
printTree(Tree);
}
void Huffman_Weight_Length(vector<Node> &Tree, ll n){
for(int i=0; i<n; ++i){
Node T = Tree[i];
while(T.parent!=-1){
T = Tree[T.parent];
Tree[i].length++;
}
}
ll sum_weight_length = 0;
for(int i=0; i<n; i++){
sum_weight_length += Tree[i].length * Tree[i].weight;
}
cout << "weight_length: " << sum_weight_length << endl;
}
vector<Node> Init_Huffman_Tree(vector<ll> A){
Node T;
vector<Node> Tree;
for(int i=0; i<A.size(); ++i){
T.weight = A[i];
T.parent = -1;
T.length = 0;
Tree.push_back(T);
}
return Tree;
}
ll find_min(vector<Node> &A){
ll min_mark = 0;
//for(min_mark=0; A[min_mark].weight!=-1; ++min_mark);
while(A[min_mark].weight==-1){
min_mark++;
}
ll Min = A[min_mark].weight;
for(int i=0; i<A.size(); ++i){
if(A[i].weight<Min&&A[i].weight!=-1){
Min = A[i].weight;
min_mark = i;
}
}
A[min_mark].weight = -1;
return min_mark;
}
void printTree(vector<Node> Tree){
for(int i=0; i<Tree.size(); ++i){
cout << Tree[i].weight << " ";
}
cout << endl;
}
void printTree_parent(vector<Node> Tree){
for(int i=0; i<Tree.size(); ++i){
cout << Tree[i].parent << " ";
}
cout << endl;
}
};
2013年机试
Problems A
问题描述:
定义一个新的斐波那契数列
F(O)=7:
F(1)=11;
F(n)=F(n-1)+F(n-2];{n>=2)
输入: 输入有多组:首先输入一个 N(N<=100),代表要输入的测试用例的个数:接下来输入N个数字 ni(ni<=100),数字间用空格隔开。
输出:
求F(n)能否被3整除,若能整除输出’yes’,否则而出’no’
样例输入:
3
0 1 2
样例输出:
no
no
yes
思路:
- 求斐波那契数列
- 看能否被3整除
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class SolutionA{
public:
void if_divided(ll n){
if(n%3 == 0) cout << "yes" << endl;
else cout << "no" << endl;
}
ll Fibonaci(ll n){
if(n==0) return 7;
if(n==1) return 11;
ll pre, pre_pre, cur;
pre_pre = 7;
pre = 7;
for(int i=2; i<=n; ++i){
cur = pre + pre_pre;
pre_pre = pre;
pre = cur;
}
}
};
Problems B
题目描述:
输入一组数据,统计每个数出现的次数,并按照数字的大小进行排序输出。
输入:
输入20个数字,数字之间用空格隔开。
输出:
统计每个数字出现的次数,并按数字的大小输出数字及其出现的次数。
样例输入:
9 8 5 1 7 2 8 2 9 10 1 7 8 9 5 6 9 0 1 9
样例输出:
0:1
1:3
2:2
5:2
6:1
7:2
8:3
9:5
10:1
思路:
用一个数组存储每个数字出现的次数,数组的索引便是该数字,数组的内容便是该数字出现的次数
代码:
1
2
3
4
5
6
7
8
9
10
class SolutionB{
public:
void number_times(ll a[]){
for(int i=0; i<100; ++i){
if(a[i]!=0){
cout << i << ":" << a[i] << endl;
}
}
}
};
Problems C
题目描述:
每个英文字母出现的频率对其进行哈弗曼编码、其中‘#’代表空格,其编码方式如下(此处略去编码方式(因为比较多不易记忆)
输入:
从文件(ecode.txt)中读入要输入的测试用例,测试用例总长度不超过 1000。
输出:
输出解码后的测试用例,包含其中的空格
思路: 因为没有文件,所以就练习一下文件读写和哈夫曼树
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
struct Node{
ll weight;
ll lchild, rchild, parent, length;
};
class SolutionC{
public:
vector<Node> HuffmanTree_Structor(vector<Node> Tree){
vector<Node> B = Tree;
Node T;
ll Min, Second_Min;
ll times = Tree.size();
for(int i=0; i<(times-1); ++i){
Min = find_min(B);
Second_Min = find_min(B);
T.weight = Tree[Min].weight + Tree[Second_Min].weight;
T.lchild = Min;
T.rchild = Second_Min;
T.parent = -1;
B.push_back(T);
Tree.push_back(T);
Tree[Min].parent = B.size()-1;
Tree[Second_Min].parent = B.size()-1;
}
return Tree;
}
vector<Node> Init_HuffmanTree(vector<ll> A){
vector<Node> Tree;
Node T;
for(int i=0; i<A.size(); ++i){
T.weight = A[i];
T.length = 0;
T.parent = -1;
Tree.push_back(T);
}
return Tree;
}
ll find_min(vector<Node> &Tree){
ll pos = 0;
while(Tree[pos].weight == -1) ++pos;
ll Min = Tree[pos].weight;
for(int i=0; i<Tree.size(); ++i){
if(Tree[i].weight<Min && Tree[i].weight != -1){
Min = Tree[i].weight;
pos = i;
}
}
Tree[pos].weight = -1;
return pos;
}
void HuffmanCode_length(vector<Node> &Tree, int n){
for(int i=0; i<n; ++i){
Node T = Tree[i];
while(T.parent != -1){
T = Tree[T.parent];
Tree[i].length++;
}
}
}
ll Huffman_weight_length(vector<Node> Tree, int n){
ll sum = 0;
for(int i=0; i<n; ++i){
sum += Tree[i].length * Tree[i].weight;
}
return sum;
}
void printHuffmanTree(vector<Node> Tree){
for(int i=0; i<Tree.size(); ++i){
cout << Tree[i].weight << " ";
}
cout << endl;
}
string file_read(string filename){
string str;
ifstream in(filename);
while(in >> str){
cout << str << endl;
}
in.close();
return str;
}
void file_write(string str){
ofstream out("test1.txt");
out << str;
out.close();
}
};
Problems D
问题描述:二进制与十进制的相互转换,输入一组数据,若为十进制,则将其转换为二进制:若为二进制则将其转换为十进制。其中所要转换的十进制与二进制的十进制大于零小于等于255。
输入:测试用例包含多组,每组有两个数n和 m,n为所输入的数值,m为输入数的进制,如 m=2,代表所输入的n是二进制数。当m和n均为零是表示输出结束。
输出:若输入的数是十进制,则将其转换为二进制;若所输入的数为二进制,则将其转换为十进制,并输出。每个结果对应一行,最后输出换行。
样例输入:
10 2
10 10
0 0
样例输出
2
1010
思路:
十进制转二进制:整数部分除基取余, 小数部分乘积取整, 因为输入仅有整数,不考虑小数部分。
二进制转十进制:各位值乘以各位权重之和
- 先将二进制数转成字符串
- 将字符串形式的二进制数转成十进制
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class SolutionD{
public:
string to_string(ll n){
string str;
while(n!=0){
str.insert(0,1,(n%10)+'0');
n /= 10;
}
return str;
}
ll B2D(ll N){
string B = to_string(N);
ll sum = 0;
ll n = 1;
for(int i=(B.length()-1); i>=0; --i){
sum += (B[i] - '0') * n;
n *= 2;
}
return sum;
}
void D2B(ll n){
vector<ll> B;
while(n!=0){
B.insert(B.begin(), n%2);
n /= 2;
}
for(int i=0; i<B.size(); ++i){
cout << B[i];
}
cout << endl;
}
};
2015年机试
Problems A
求一串数中大于1的素数之和
输入不超过100个数 不超过10 组 输入0结束
例:
输入
4 1 2 3 4
5 1 2 3 4 5
0
输出
5
10
思路:
- 用字符串一行一行地读入,再将字符串转成整型。
- 依次判断是否是素数,并判断是否重复,若不重复,存入vector。
- 求和输出。
此题收获在于不容易判断换行符时,读入一行数据的处理方式
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
class SolutionA{
public:
void ProblemsA(){
string line;
vector<ll> A;
while(1){
getline(cin, line);
if(line[0]=='0') break;
cout << prime_num_sum(str2vec(line)) << endl;
}
}
ll prime_num_sum(vector<ll> A){
vector<ll> prime_nums;
for(int i=0; i<A.size(); ++i){
if(if_prime_number(A[i])){
vector<ll>::iterator pos = find(prime_nums.begin(), prime_nums.end(), A[i]);
if(pos == prime_nums.end()) prime_nums.push_back(A[i]);
}
}
ll sum = 0;
for(int i=0; i<prime_nums.size(); ++i){
sum += prime_nums[i];
}
return sum;
}
bool if_prime_number(ll n){
if(n==0 || n==1) return 0;
ll i = 2;
while(i!=n){
if(n%i==0) return 0;
i++;
}
return 1;
}
vector<ll> str2vec(string line){
vector<ll> A;
for(int i=0; i<line.size(); ++i){
if(line[i]>'0' && line[i]<='9'){
A.push_back(line[i] - '0');
}
}
return A;
}
};
Problems B
压缩字符串
输入只含A-Z的字符串 不超过1000个字母将连续相同字母压缩为重复次数+字母(这个 忘记是多组输入还是单组了)
例:
输入
ABBCCC
输出
A2B3C
思路:
- 通过两个指针pre和i, 计算相同字符地个数
- 如果个数大于1,进行替换
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class SolutionB{
public:
void ProblemsB(){
string str;
getline(cin, str);
ll pre = 0;
ll Size = str.size();
for(int i=1; i<Size; ++i){
if(str[pre]==str[i]) continue;
else{
if(i-pre>1){
char c = str[i-1];
str.erase(str.begin()+pre, str.begin()+i-1);
str.insert(pre, 1, i-pre+'0');
str.insert(pre+1, 1, c);
}
pre = i;
}
}
if(Size-pre>1){
char c = str[Size-1];
str.erase(str.begin()+pre, str.begin()+Size-1);
str.insert(pre, 1, Size-pre+'0');
str.insert(pre+1, 1, c);
}
cout << str << endl;
}
};
注意,当i指针到了最后的时候,最后一部分还没有进行替换,要单独替换一次。
这里string中用erase的方法不对, str.erase(pos, n)删除从pos开始的n个字符, 结果正确只是碰巧。
Problems C
Problems C: 机器人走迷宫
迷宫由 N W S E 组成 踩到N向上走一格 踩到W向左走一格 踩到S向下走一格 踩到E向右走一格
输入迷宫行数、列数(不大于10)、机器人初始列数(注意这个列数是从1开始数的)
判断能否走出迷宫。能走出输出步数
多组输入 遇 0 0 0 结束输入
例
输入
4 6 5
NNNNSN
NNNSWN
NNSWNN
NSWNNN \
3 5 2
NSNNN
NSWNN
NENNN \
0 0 0
输出
7
No
思路:
- 创建一个结构体,存储迷宫节点的应走的方向,和是否访问过
- 利用结构体创建迷宫矩阵。
- 根据初始位置走迷宫,当超出上、左、右三边界或者走到已经访问过的节点时,不能走出迷宫。
- 若超出下边界,可走出迷宫
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
struct maze{
bool passed;
char direction;
// maze(bool x, char d): passed(x), direction(d){
// }
};
class SolutionC{
public:
void ProblemsC(){
ll m, n, init_col;
while(cin >> m >> n >> init_col){
if(m==0&&n==0&&init_col==0) return;
char t;
vector<vector<char> > M;
vector<char> N;
for(int i=0; i<m; ++i){
for(int j=0; j<n; ++j){
cin >> t;
N.push_back(t);
}
M.push_back(N);
N.erase(N.begin(), N.end());
}
vector<vector<maze> > Maze;
Maze = CreateMaze(m, n, M);
play(Maze, init_col-1);
}
}
void play(vector<vector<maze> > Maze, ll init_col){
ll i = 0, j = init_col;
ll counter = 0;
while(1){
if(Maze[i][j].passed==1){
cout << "No" << endl;
cout << "because of me" << endl;
return;
}
Maze[i][j].passed = 1;
++counter;
if(Maze[i][j].direction=='N'){
--i;
if(i<0 || j<0 || j>Maze[0].size()-1){
cout << "No" << endl;
return;
}
if(i>Maze.size()-1){
cout << counter << endl;
return;
}
continue;
}
if(Maze[i][j].direction=='S'){
++i;
if(i<0 || j<0 || j>Maze[0].size()-1){
cout << "No" << endl;
return;
}
if(i>Maze.size()-1){
cout << counter << endl;
return;
}
continue;
}
if(Maze[i][j].direction=='W'){
--j;
if(i<0 || j<0 || j>Maze[0].size()-1){
cout << "No" << endl;
return;
}
if(i>Maze.size()-1){
cout << counter << endl;
return;
}
continue;
}
if(Maze[i][j].direction=='E'){
++j;
if(i<0 || j<0 || j>Maze[0].size()-1){
cout << "No" << endl;
return;
}
if(i>Maze.size()-1){
cout << counter << endl;
return;
}
continue;
}
}
}
vector<vector<maze> > CreateMaze(ll m, ll n, vector<vector<char> > M){
vector<vector<maze> > Maze;
vector<maze> N;
maze T;
for(int i=0; i<m; ++i){
for(int j=0; j<n; ++j){
T.passed = 0;
T.direction = M[i][j];
N.push_back(T);
}
Maze.push_back(N);
N.erase(N.begin(), N.end());
}
return Maze;
}
void printMaze(vector<vector<maze> > Maze){
for(int i=0; i<Maze.size(); ++i){
for(int j=0; j<Maze[i].size(); ++j){
cout << Maze[i][j].direction << ' ';
}
cout << endl;
}
cout << endl;
}
};
Problems D
从文件Score.txt中读取学生信息,对其进行排序,学生信息包括学号不高于20位,题目数不超过10, 分数, 首先按照回答题数从大往小排,题数一样按照分数从小往大排。
例
文件内容:
CS00000001 4 110
CS00000002 4 120
CS00000003 5 150
输出
1 CS00000003 5 150
2 CS00000001 4 110
3 CS00000002 4 120 \
思路:
- 创建学生信息结构体
- 读入学生信息(将subjects和scores等从string转成整型)
- 按照subjects对学生信息进行排序(快排)
- 利用两个指针pre和i对subjects相同的学生,按照scores进行排序(快排)
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
struct Info{
string ID;
ll subjects;
ll scores;
};
class SolutionD{
public:
void Information_Sort(){
vector<Info> info = Init_Students_Info();
QuickSort(0, info.size()-1, info, "subjects");
ll pre = 0;
for(int i=1; i<info.size(); ++i){
if(info[pre].subjects == info[i].subjects) continue;
if(info[pre].subjects != info[i].subjects){
QuickSort(pre, i-1, info, "scores");
pre = i;
}
}
// 将剩下的最后一组排序
QuickSort(pre, info.size()-1, info, "scores");
for(int i=0; i<info.size(); ++i){
cout << info[i].ID << ' ' << info[i].subjects
<< ' ' << info[i].scores <<endl;
}
}
void QuickSort(ll i, ll j, vector<Info> &info, string str){
if(i<j){
if(str=="subjects"){
ll pos = Partition_subjects(i, j, info);
QuickSort(i, pos-1, info, "subjects");
QuickSort(pos+1, j, info, "subjects");
}
if(str=="scores"){
ll pos = Partition_scores(i, j, info);
QuickSort(i, pos-1, info, "scores");
QuickSort(pos+1, j, info, "scores");
}
}
}
ll Partition_subjects(ll low, ll high, vector<Info> &info){
Info k = info[low];
while(low<high){
while(low<high&&info[high].subjects<=k.subjects) --high;
info[low] = info[high];
while(low<high&&info[low].subjects>k.subjects) ++low;
info[high] = info[low];
}
info[low] = k;
return low;
}
ll Partition_scores(ll low, ll high, vector<Info> &info){
Info k = info[low];
while(low<high){
while(low<high&&info[high].scores>=k.scores) --high;
info[low] = info[high];
while(low<high&&info[low].scores<k.scores) ++low;
info[high] = info[low];
}
info[low] = k;
return low;
}
vector<Info> Init_Students_Info(){
ifstream in("Score.txt");
string info;
vector<Info> information;
Info S;
while(getline(in, info)){
ll pos = info.find(' ');
S.ID.assign(info, 0, pos);
info.erase(0, pos+1);
pos = info.find(' ');
string sub = string(info, 0, pos);
S.subjects = str2num(sub);
info.erase(0, pos+1);
S.scores = str2num(info);
information.push_back(S);
}
return information;
}
ll str2num(string str){
ll sum = 0;
for(int i=0; i<str.size(); ++i){
sum = sum*10 + str[i] - '0';
}
//cout << sum << endl;
return sum;
}
};
注意,两个指针也存在上面一题的问题,当i指针指到最后,还有一组数据没有排序,要单独排序一次
2018年机试
这一年的题我感觉还是有点难度,如果这一年我上机的话,可能最多就做出来三道。
Problems C的面积计算我想的有些复杂,学长算法很巧妙,值得学习。
Problems D我没想到好的比较日期的方法,硬比也能比出来,但是有些麻烦, 后来借鉴网上做法。
Problems A
近来、跳一跳这款小游戏风靡全国,受到不少玩家的喜爱。
简化后的跳一跳规则如下:玩家每次从当前方块跳到下一个方块,如果没有跳到下一个方块上则游戏结束。
如果跳到了方块上,但没有跳到方块的中心则获得1分:跳到方块中心时,若上一次的得分为1分或这是本局游戏的第一次跳跃则此次得分为2分,否则此次得分比上一次得分多两分(即连续跳到方块中心时,总得分将+2,+4,+6,+8.)。
现在给出一个人跳一跳的全过程,请你求出他本局游戏的得分(按照题目描述的规则)。
输入格式
输入包含多个数字,用空格分隔,每个数字都是1,2,0之一,1表示此次跳跃跳到了方块上但是没有跳到中心,2表示此次跳跃跳到了方块上并且跳到了方块中心,0表示此次跳跃没有跳到方块上(此时游戏结束)。
输出格式 \ 输出一个整数,为本局游戏的得分(在本题的规则下)
样例输入
1 1 2 2 2 1 1 2 2 0
样例输出
22
数据规模和约定
对于所有测评用例,输入的数字不超过30个, 保证0正好出现一次且为最后一个数字
思路:
需要有一个变量last_scores记录上一次跳得了多少分
判断跳到什么位置
- 若跳到1, 总分加1,last_socres清零
- 若跳到2,总分加上2再加上last_scores, 同时last_socres加二
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class SolutionA{
public:
void ProblemsA(){
vector<ll> A;
ll n;
while(cin >> n){
A.push_back(n);
if(n==0) break;
}
play(A);
}
void play(vector<ll> A){
ll last_scores = 0, sum=0;
for(int i=0; i<A.size(); ++i){
if(A[i]==1){
sum+=1;
last_scores = 0;
}
if(A[i]==2){
sum += (last_scores + 2);
last_scores += 2;
}
if(A[i]==0){
cout << sum << endl;
}
}
}
};
Problems B
问题描述:
给出一个字符串和多行文字,在这些文字中找到字符串出现的那些行。你的程序还 需支持大小写敏感选项;当选项打开时,表示同一个字母的大写和小写看作不同的 字符;当选项关闭时,表示同一个字母的大写和小写看作相同的字符。
输入格式:
输入的第一行包含一个字符串s,由大小写英文字母组成。
第二行包含一个数字,表示大小写敏感的选项,当数字为0时表示大小写不敏感,当数字为1时表示大小写敏感。
第三行包含一个整数n,表示给出的文字的行数。
接下来n行,每行包含一个字符串,字符串由大小写英文字母组成,不含空格和其他 字符。
输出格式:
输出多行,每行包含一个字符串,按出现的顺序依次给出那些包含了字符串S的行。
样例输入:
Hello
1
5
HelloWorld
HiHiHelloHiHi
GrepIsAGreatTool
HELLO
HELLOisNOTHello
样例输出:
HelloWorld
HiHiHelloHiHi
HELLOisNOTHello
思路:
此题收获在,帮我复习了kmp算法, 以及对于大小写敏感的处理。
使用find函数或者使用kmp算法查找子字符串, 若大小写不敏感,将字符串统一转为大写或小写。 若敏感, 正常处理即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
class SolutionB{
public:
void ProblemsB(){
string Substr;
ll if_sens;
ll n;
getline(cin, Substr);
cin >> if_sens >> n;
string str;
cin.ignore();
for(int i=0; i<n; ++i){
getline(cin, str);
if(!if_sens){
string str_ = str2str(str);
Substr = str2str(Substr);
int pos = str_.find(Substr, 0);
if(pos != -1) cout << str << endl;
}
else{
int pos = str.find(Substr, 0);
if(pos != -1) cout << str << endl;
}
}
}
// 统一将字符串变为小写
string str2str(string str){
for(int i=0;i<str.size(); ++i){
if(str[i]>='A' && str[i]<='Z'){
str[i] += 'a' - 'A';
}
}
return str;
}
int KMP(string S, string T, ll Next[]){
S.insert(0, 1, '0');
T.insert(0, 1, '0');
int i = 1;
int j = 1;
while(i<=S.length()&&j<=T.length()){
if(j==0 || S[i]==T[j]){
cout << S[i] << " " << T[j] << endl;
++i; ++j;
}
else{
j = Next[j];
}
}
if(j>T.length())
return (i - T.length()-1);
return -1;
}
void getNext(string S, ll Next[]){
S.insert(0, 1, '0');
int i = 1;
int j = 0;
Next[1] = 0;
while(i<=S.length()){
if(j==0||S[i]==S[j]){
++i; ++j; Next[i] = j;
}
else{
j = Next[j];
}
}
}
};
Problems C
问题描述:
在一个定义了直角坐标系的纸上, 画一个(x1, y1)到(x2, y2)的矩形指将横坐标
范围从x1到x2,纵坐标范围从y1到y2之间的区域涂上颜色。
图给出了一个画了两个矩形的例子。第一个矩形是(1,1)到(4,4),用绿色和紫色表示 第二个矩形是(2.3)到(6,5),用蓝色和紫色表示。图中,一共有15个单位的面积被涂 上颜色, 其中紫色部分被涂了两次,但在计算面积时只计算一次。在实际的涂色过 程中,所有的矩形都涂成统一的颜色,图中显示不同颜色仅为说明方便。
出所有要画的矩形,请问总多个单位的面积被涂上颜色。
输入格式
输入的第一行包含一个整数n,表尔要画的矩形的个数。
接下来 n 行,每行4个非负整数,分别表示要画的矩形的左下角的横坐标与纵坐标,以
及右上角的横坐标与纵坐标。
输出格式
输出一个整数,表示有少个单位的面积被涂上颜色。
样例输入
2
1 1 4 4
2 3 6 5
样例输出
15
思路:
总体思路就是每个矩形的面积相加, 在减去重叠部分的面积。
但是我一开始的想法有点复杂,需要判断两个矩形的相对位置,情况就很多。
借鉴学长的算法,利用一个矩阵来标记每一块是否被计算过,这种处理方法值得学习。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
struct pos{
ll x1;
ll y1;
ll x2;
ll y2;
};
class SolutionC{
public:
void ProblemsC(){
ll n;
pos p;
bool flag[100][100];
cin >> n;
ll S = 0;
while(n--){
cin >> p.x1 >> p.y1 >> p.x2 >> p.y2;
cout << p.x1 << " " << p.y1 << " "
<< p.x2 << " " << p.y2 << endl;
S += cal_S(p);
for(int i=p.x1; i<p.x2; ++i){
for(int j=p.y1; j<p.y2; ++j){
if(flag[i][j]==1)
S--;
flag[i][j] = 1;
}
}
}
cout << S << endl;
}
int abs(ll a, ll b){
if(a > b) return a - b;
else return b - a;
}
int cal_S(pos p){
int width = abs(p.x2, p.x1);
int height = abs(p.y2, p.y1);
return height * width;
}
};
Problems D
问题描述:
给定一组记录n(n<100)小明各个时期的考试成绩, 格式为日期+成绩, 中间以空格
隔开, 记录之间分行输入,例如
2008/6/3 80
2009/1/1 56
其中日期输入要求年份1996-2100 月份1-12 日期1-31
现要求以分数为关健字从大到1小对其进行排序,若分数相同则按日期从小到大排序
输入样例
4
2017/1/1 95
2017/6/10 85
2017/3/2 95
2017/1/1 65
输出样例
2017/1/1 95
2017/3/2 95
2017/6/10 85
2017/1/1 65
思路:
此题收获在于如何判断日期,以及sort的使用方法。
但是我的解法仍有写完善,没有判断日期的有效性, 这个并不复杂。
- 先按照分数进行排序
- 对日期相同的,再按照日期进行排序
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
struct Info{
int year;
int month;
int day;
int scores;
};
bool compare_scores(Info a, Info b){
return a.scores > b.scores;
}
bool compare_date(Info a, Info b){
if(a.year==b.year){
if(a.month==b.month){
return a.day < b.day;
}else{
return a.month < b.month;
}
}
else return a.year < b.year;
}
class SolutionD{
public:
void ProblemsD(){
vector<Info> info;
Info temp;
int year, month, day, scores;
int n;
cin >> n;
while(n--){
scanf("%d/%d/%d %d", &year, &month, &day, &scores);
temp.year = year;
temp.month = month;
temp.day = day;
temp.scores = scores;
info.push_back(temp);
}
sort(info.begin(), info.end(), compare_scores);
ll pre = 0;
for(int i=1; i<info.size(); ++i){
if(info[i].scores==info[pre].scores) continue;
if(info[i].scores!=info[pre].scores){
sort(info.begin()+pre, info.begin()+i, compare_date);
}
}
for(int i=0; i<info.size(); ++i){
printf("%d/%d/%d %d\n", info[i].year, info[i].month, info[i].day, info[i].scores);
}
}
注意,compare函数不能写再类里面。
2019年机试
ProblemsA
问题描述:
给定一个整数数列,数列中连续相同的最长整数序列算成一段,问数列中共
有多少段?
输入格式:
输入的第一行包含一个整数n,表示数列中整数的个数。
第二行包含n个整数a1, a2, …, an,表示给定的数列,相邻的整数之间用一
个空格分隔。
输出格式:
输出一个整数,表示给定的数列有多个段。
样例输入
8
8 8 8 0 12 12 8 0 \
样例输出
5
样例说明:
8 8 8是第一段,0是第二段,12 12是第三段,倒数第二个整数8是第四段,
最后一个0是第五段。
解题思路:
一个计数器counter, 两个指针,当两指针内容不同的是计数器加一
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class SolutionA {
public:
void ProblemA() {
int n;
ll c;
vector<ll> a;
cin >> n;
while (n--) {
cin >> c;
a.push_back(c);
}
int pre = 0;
int counter = 1;
for (int i = 1; i < a.size(); ++i) {
if (a[pre] != a[i]) {
counter++;
pre = i;
}
}
cout << counter << endl;
}
};
ProblemsB
问题描述
给定n个整数,请统计出每个整数各位数字和,按出现数字和从大到小的顺序输出。
输入格式
输入的第一行包含一个整数n,表示给定数字的个数。 \
第二行包含n个整数,相邻的整数之间用一个空格分隔,表示所给定的整数。
输出格式
输出多行,每行包含两个整数,分别表示一个给定的整数和它出现的各位数字和。按出现次数递减的顺序输出。如果两个整数出现的各位数字和相同,则先输出值较小的,然后输出值较大的。
样例输入
5
101 100 999 1234 110
样例输出
999 27
1234 10
101 2
110 2
100 1
解题思路:
创建一个结构体,存储数和各位和。
写一个函数将数字各位转成vector, 计算各位和。
根据各位和将结构体vector排序。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
struct N {
ll num;
ll sum;
};
bool compare(N a, N b) {
if (a.sum == b.sum) return a.num < b.num;
return a.sum > b.sum;
}
class SolutionB {
public:
void ProblemB() {
int n = 0;
cin >> n;
N c;
vector<N> numVec;
while (n--) {
cin >> c.num;
vector<ll> num = int2vec(c.num);
c.sum = SumOfVec(num);
numVec.push_back(c);
}
sort(numVec.begin(), numVec.end(), compare);
for (int i = 0; i < numVec.size(); ++i) {
cout << "num: " << numVec[i].num << " "
<< "sum: " << numVec[i].sum << endl;
}
}
vector<ll> int2vec(ll n) {
vector<ll> num;
while (n != 0) {
num.insert(num.begin(), n % 10);
n = n / 10;
}
return num;
}
ll SumOfVec(vector<ll> num) {
ll sum = 0;
for (int i = 0; i < num.size(); ++i) {
sum += num[i];
}
return sum;
}
};
ProblemsC
问题描述
消除类游戏是深受大众欢迎的一种游戏,游戏在一个包含有n行m列的游戏棋盘 上进行,棋盘的每一行每一列的方格上放着一个有颜色的棋子,当一行或一列上有连续三个或更多的相同颜色的棋子时,这些棋子都被消除。当有多处可以被消除时,这些地方的棋子将同时被消除。
请注意:一个棋子可能在某一行和某一列同时被消除。
输入的第一行包含两个整数n, m,用空格分隔,分别表示棋盘的行数和列数。
接下来n行,每行m个整数,用空格分隔,分别表示每一个方格中的棋子的颜色。颜色使用1至9编号。
输出n行,每行m个整数,相邻的整数之间使用一个空格分隔,表示经过一次消除后的棋盘。如果一个方格中的棋子被消除,则对应的方格输出0,否则输出棋子的颜色编号。
输入样例:
第一组:
4 5
2 2 3 1 2
3 4 5 1 4
2 3 2 1 3
2 2 2 4 4
第二组:
4 5
2 2 3 1 2
3 1 1 1 1
2 3 2 1 3
2 2 3 3 3
输出结果示例:
第一组:
2 2 3 0 2
3 4 5 0 4
2 3 2 0 3
0 0 0 4 4
第二组:
2 2 3 0 2
3 0 0 0 0
2 3 2 0 3
2 2 0 0 0
解题思路:
要创建一个矩阵副本(get trick:以后遇到类似改变值的问题, 都可使用副本来解决), 原矩阵行或列三个相同,则将副本对应的位置置0.
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class SolutionC {
public:
void ProblemC() {
int n, m, c;
cin >> n >> m;
int M[n][m], M1[n][m];
for (int i = 0; i < n; ++i) {
for (int j = 0; j < m; ++j) {
cin >> c;
M[i][j] = c;
M1[i][j] = c;
}
}
for (int i = 0; i < n; ++i) {
for (int j = 0; j < m; ++j) {
if (M[i][j] == M[i][j + 1] && M[i][j + 1] == M[i][j + 2]) {
M1[i][j] = 0;
M1[i][j + 1] = 0;
M1[i][j + 2] = 0;
}
}
}
for (int j = 0; j < m; ++j) {
for (int i = 0; i < n; ++i) {
if (M[i][j] == M[i + 1][j] && M[i + 1][j] == M[i + 2][j]) {
M1[i][j] = 0;
M1[i + 1][j] = 0;
M1[i + 2][j] = 0;
}
}
}
for (int i = 0; i < n; ++i) {
for (int j = 0; j < m; ++j) {
cout << M1[i][j] << " ";
}
cout << endl;
}
}
};
ProblemsD
题目描述:
定义每个游戏由4个从1-9的数字和三个四则运算符组成,保证数字运算符将数字两两隔开,不存在括号和其他字符,运算顺序按照四则运算顺序进行。其中加法用符号‘+’表示,减法用符号‘-’表示,乘法用小写字母’x’表示,除法用符号’/’表示,在游戏里除法为整除,例如2/3=0,3/2=1,4/2=2。
给出一个符合上述定义的表达式,请求出表达式的值
输入说明:
输入是一个长度为7的字符串, 表示一个表达式
输出说明:
输出一个整数,表示表达式求值的结果
输入样例:
9+3+4x3
1x9-5/9
输出样例:
24
9
解题思路:
复杂点的计算可以使用逆波兰计算器,但此题用不到。
一个数字栈,一个符号栈。
数字依次进栈。
遇到符号‘-’, 将减法变加法,易于处理。 计算时,不必拘泥于一个元素一个元素地处理。
遇到乘除,直接算出结果, 结果入栈。因为优先级只有两种。
最后,符号栈依次退栈, 计算数字栈之和。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
class SolutionD {
public:
void ProblemD() {
string s;
getline(cin, s);
calculate(s);
}
int calculate(string s) {
stack<ll> num;
stack<char> sign;
for(int i=0; i<s.size(); ++i){
if(s[i]>='0' && s[i] <='9'){
num.push(s[i]-'0');
}else{
if(s[i]=='+'){
sign.push(s[i]);
}
// 以下做法思路可借鉴,将减法转为加法
// 且不拘泥于一个元素一个元素处理
if(s[i]=='-'){
num.push((s[i+1] - '0') * (-1));
sign.push(s[i]);
++i;
}
if(s[i]=='x'){
ll a = num.top(); num.pop();
ll b = s[i+1] - '0';
num.push(a*b);
++i;
}
if(s[i]=='/'){
ll a = num.top(); num.pop();
ll b = s[i+1] - '0';
num.push(a/b);
++i;
}
}
}
while(!sign.empty()){
sign.pop();
ll a = num.top(); num.pop();
ll b = num.top(); num.pop();
num.push(a+b);
}
cout << num.top() << endl;
}
};
CCF部分题目
201912-1报数

思路:
A, B, C, D四个变量记录甲乙丙丁跳过的次数
取余判断是否为7倍数, 转字符串判断是否有7
再对4取余,看是谁报数, 相应的计数器加一
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
---------------------------------------------*/
class Solution{
public:
void Problem(){
ll counter_A=0, counter_B=0, counter_C=0, counter_D=0;
//记录报数的次数。
ll counter = 0;
ll i = 1;
int n;
cin >> n;
while(counter!=n){
if((i%7==0) || contain7(i)){
if(i%4==1) ++counter_A;
if(i%4==2) ++counter_B;
if(i%4==3) ++counter_C;
if(i%4==0) ++counter_D;
i++;
continue;
}
++counter;
++i;
}
cout << counter_A << endl;
cout << counter_B << endl;
cout << counter_C << endl;
cout << counter_D << endl;
}
bool contain7(ll i){
while(i!=0){
if(i%10==7) return 1;
i = i/10;
}
return 0;
}
};
201912-2

思路:
结构体+map 可以替代矩阵, 可以解决边缘问题和负数问题
用一个count来计数周围有几坨垃圾
结构体内部需要重载小于号才能封装到map中。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
const int N = 1e3 + 1;
struct node {
int x, y;
node() {}
node(int a, int b) : x(a), y(b) {}
bool operator<(const node &oth) const {
if (x != oth.x) return x < oth.x;
return y < oth.y;
}
} h[N];
class Solution {
public:
void Problem() {
map<node, bool> mp;
int score[5] = {0};
int n;
int x, y;
cin >> n;
for (int i = 0; i < n; ++i) {
cin >> x >> y;
h[i] = node(x, y);
mp[h[i]] = 1;
}
for (int i = 0; i < n; ++i) {
int count = 0;
x = h[i].x;
y = h[i].y;
if (mp[node(x + 1, y)] && mp[node(x - 1, y)] &&
mp[node(x, y + 1)] && mp[node(x, y - 1)]) {
count = mp[node(x - 1, y - 1)] + mp[node(x - 1, y + 1)] +
mp[node(x + 1, y - 1)] + mp[node(x + 1, y + 1)];
score[count] += 1;
}
}
for (int i = 0; i < 5; ++i) {
cout << score[i] << endl;
}
}
};