论文部分
Abstract
生成对抗网络是很强大的生成模型,但是却有着训练不稳定的问题。最近提出的Wasserstein GAN (WGAN)使得训练GAN取得了进步, 但是有时仍然会产生不好的样本或者难以收敛。 我们发现这些问题通常是WGAN中的权重截断的结果,这会导致不良的表现。 我们提出一种权重截断的替代方法。我们提出的方法比标准的WGAN有更好的表现,并且让更广泛的GAN结构在没有超参数微调的情况下更稳定的训练, 包括101层的ResNet和具有连续生成器的语言模型。我们也在CIFAR-10和LSUN卧室的数据集上取得了高的质量。
Introduction
生成对抗网络是一类强大的生成模型, 它让生成模型像两个网络之间的游戏:一个生成网络给定一定噪声产生合成的数据, 一个判决网络判别生成器的输出和真实的数据。GANs能够产生非常真实的样本,但是难以训练, 并且最近很多关于这个课题的作品开始致力于找到稳定训练的方法。尽管这样, 连续稳定地训练GANs仍然是一个开放的问题。
WGAN充分利用了Wasserstein距离产生了一个价值函数, 这个价值函数在理论上优于原版的价值函数。WGAN要求判决器的参数必须在1-Lipschitz函数的空间, 作者通过权重截断来实现这个目标。
我们的贡献如下:
- 在toy数据集上,我们展示了判决器的权重截断是如何导致不良的表现的。
- 我们提出梯度惩罚(WGAN-GP), 它没有上述的问题。
- 我们展示了各种各样GAN结构的稳定训练, 比权重截断表现得更好, 高质量的图像生成和一个没有任何离散采样的字符级别的GAN语言模型
Background
Generative adversarial networks
生成对抗网络的优化目标如下:
\[\min_G \max_D E_{x \thicksim P_r}[log (D(x))] + E_{\tilde x \thicksim P_g}[log (1 - D(\tilde x))] \tag 1\]如果在G更新参数之前,D训练地太好了,最小化价值函数去最小化$P_r$和$P_g$之间的JS散度, 但这么做常常会导致梯度消失, 因为D训练地已经饱和了。后来,进而提出的通过最大化$E_{\tilde x \thicksim P_g}[log (D(\tilde x))]$训练生成器, 在一定程度上避免了这种困难。 然而,在一个好的判决器的情况下, 即便是这个修改过的损失函数也会导致判决器产生不好的表现。
Wasserstein GANs
WGAN的价值函数如下:
\[\min_G \max_{D \in 1-Lipschitz} E_{x \thicksim P_r}[D(x)] - E_{\tilde x \thicksim P_g}[D(\tilde x)] \tag 2\]WGAN的很好的属性是它的价值函数和样本的生成质量相关,这是GANs所没有的。
在判决器上的Lipschitz约束,使用权重截断使得判决器的参数限制在[-c, c]的空间。 我们接下来将会展示这种方式的问题以及提出一种替代的方式。
Properties of the optimal WGAN critic
推论1:
经过1-Lipschitz约束的函数f,它的梯度范数在分布$P_r$和$P_g$下几乎处处是1。
Difficulties with weight constraints
我们发现,WGAN中的权重截断会导致优化困难,并且即使优化成功,所产生的判决器也可能具有pathlogical value surface。
我们的实验使用了WGAN中的权重截断的方式来限制权重,我们也尝试了其他的权重限制(L2范数截断, 权重规范化)以及权重衰减,它们表现出相似的问题。
在一定程度上可以在判决器中用BathNorm来缓解这些问题。然而即便有BatchNorm, 我们观察到很深的WGAN的判决器常常难以收敛。
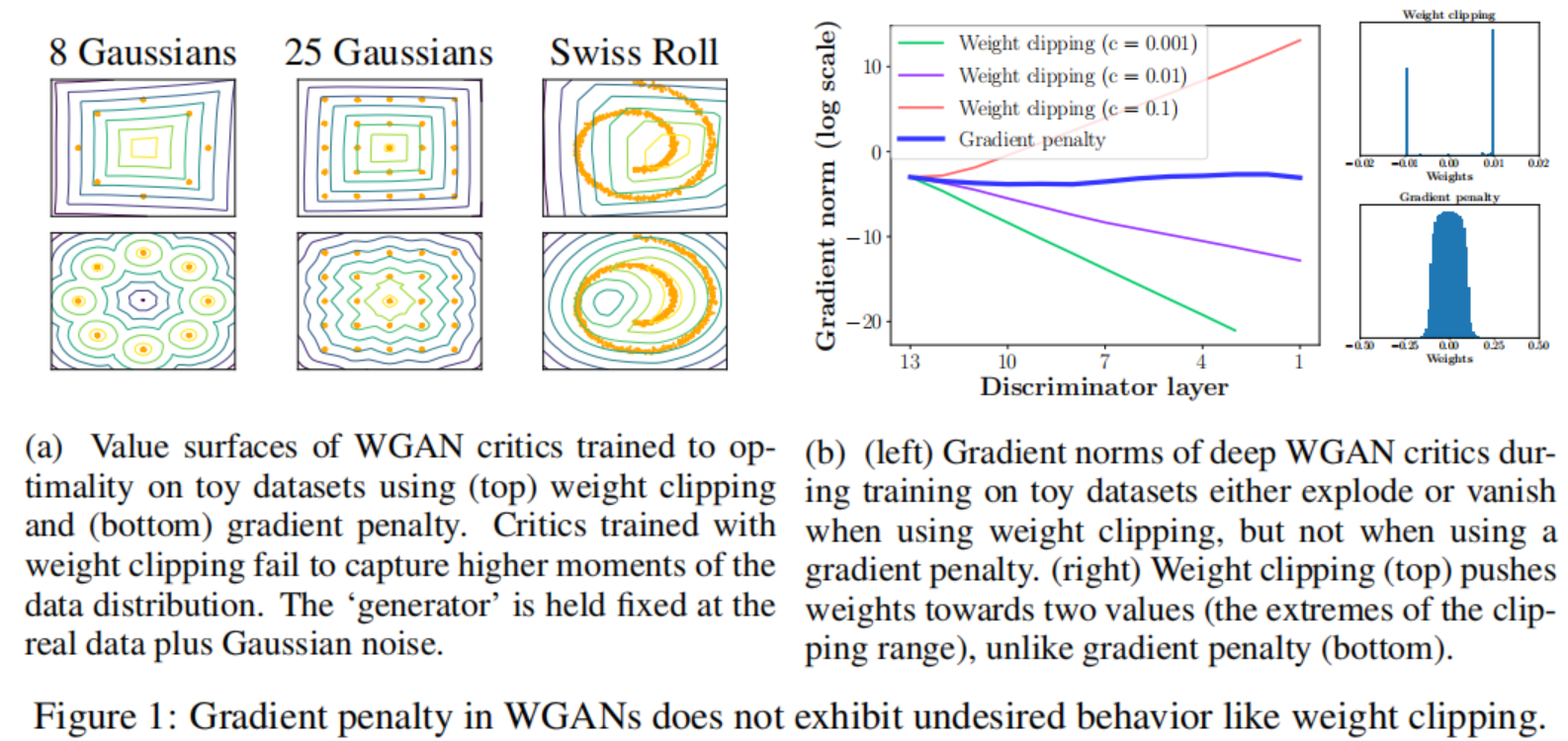
Capacity underuse
通过权重截断实现k-Lipshitz约束会使判决器偏向一个简单得多的函数。如推论1所述, 在权重截断限制情况下, 最优的WGAN判决器在$P_r$和$P_g$的分布下几乎处处有单位梯度范数, 我们观察到我们的神经网络结构想要尽可能的获取最大的梯度范数k, 最终学习到一个非常简单的函数。
Exploding and vanishing gradients
我们观察到WGAN的优化过程之所以困难是因为权重限制和代价函数的互相影响, 这导致了梯度爆炸和梯度消失在没有细心地调整阶段阈值c的情况下。
Gradient penalty
我们现在提出一种替代的方式来实现Lipschitz约束。 一个函数当且仅当它的梯度范数处处为1时,它是1-Lipschitz, 因此我们认为对判决器的每一个输入直接限制判决器的输出的梯度范数。为了避免易处理性问题,我们实现这个约束在随机采样的$\hat x \thicksim P_{\hat x}$的梯度范数上加上一个惩罚。我们新的目标函数如下:
\[L = E_{\tilde x \thicksim P_g}[D(\tilde x)] - E_{x \thicksim P_r}[D(x)] + \lambda E_{\hat x \thicksim P_{\hat x}}[(\| \nabla_{\hat x} D(\hat x) \|_2 - 1)^2] \tag 3\]$\nabla$表示求导, $P_{\hat x}$表示从$P_r$和$P_g$两个分布之间的这片分布采样,为什么呢?因为x理论上是应该包含所有包含对判决器产生实际影响的区域, 考虑到整个WGAN 的目的是让$𝑃_𝐺$渐渐向$𝑃_{𝑑𝑎𝑡𝑎}$靠拢,那位于$𝑃_𝐺$和$𝑃_{𝑑𝑎𝑡𝑎}$之间的区域一定会对判别器产生实质的影响。
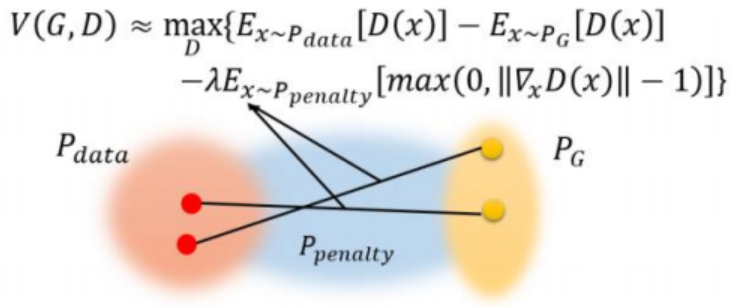
$\hat x$是通过这样得到的:
\[\hat x = \epsilon x + (1 - \epsilon)\tilde x\]为什么这么做?我们观察(3)
\[[(\| \nabla_{\hat x} D(\hat x) \|_2 - 1)^2]\]这一项是一个非负数,我们要最小化L, 那么这个非负数就不会太大, 也就是
\[\| \nabla_{\hat x} D(\hat x) \|_2\]会在1附近。
这里我们回顾1-Lipschtiz函数的推论1, 经过1-Lipschitz约束的函数f,它的梯度范数在分布$P_r$和$P_g$下几乎处处是1。
那么我们的这一项的目的就是对于D的定义域上的x, 使它的梯度范数为1, 相当于稳住了梯度, 我们的目的就达到了。
No critic batch normalization:大多数的之前GAN都会在生成器和判决器上使用BatchNorm来稳定训练。我们的惩罚训练目标不适用于这种设置, 因为我们对每个输入单独地惩罚判决器的梯度范数, 而不是整个batch。 为了解决这个问题,在我们的模型中删去判决器的BatchNorm, 发现它表现得很好。我们的方法在带有不引进样本之间相关性的Norm方式时依然有效。特别地,我们推荐LayerNorm取代BatchNorm。
Two-sided penalty:我们鼓励梯度范数趋向于1(two-sided penalty), 而不是总是小于1(one-sided penalty)。经验上这似乎没有约束判决器太多, 很可能时因为最优的WGAN判决器在$P_r$和$P_g$以及它们之间的区域$P_{penalty}$下总有梯度范数为1。

实现部分
Reference
- Gulrajani I, Ahmed F, Arjovsky M, et al. Improved training of wasserstein gans[C]//Advances in neural information processing systems. 2017: 5767-5777.
- 关于WGAN-GP的理解
- 关于WGAN-GP中的遗留问题?
- wgan-gp/gan_cifar10.py