范数

简单理解， 范数度量某个向量空间（或矩阵）中的每个向量的长度或大小，是对矩阵和向量的一种描述，有了描述那么“大小就可以比较了”。

比如：8 和 24，一目了然，24 大；但对于 1 维张量，即向量A (1,2,8) 和 B (2,3,5) 哪个大？

所以通过使用范数，比如：L-2范数，计算欧式距离，来比较大小，向量 A = 69，B = 38，所以向量 A 大。

范数的本质是距离，存在的意义是实现比较

• 0范数表示向量中非零元素的个数（即为其稀疏度）。
• 1范数表示为，绝对值之和。
• 2范数则指模。

协方差偏移（Covariate Shift）

在训练的时候，前面层训练参数的更新将导致后面层输入数据分布的变化。以网络第二层为例：网络的第二层输入，是由第一层的参数和input计算得到的，而第一层的参数在整个训练过程中一直在变化，因此必然会引起后面每一层输入数据分布的改变。我们把网络中间层在训练过程中，数据分布的改变称之为：“Internal Covariate Shift”。

损失函数

L1 loss

L2 loss

TV loss

即求每一个像素和横向下一个像素的差的平方，加上纵向下一个像素的差的平方， 然后开$\beta / 2$次根。

GAN

代码实现：

G_Loss:

1
G = BCE(D(G(z)), real_label)

D_Loss:

1
2
3
D_real = BCE(D(x), real_label)
D_fake = BCE(D(G(z).detach()), fake_label)
D = D_real + D_fake

WGAN

其中$|D|_L \leq 1$表示判决器D满足$1-lipchitz$范数。

代码实现：

G_Loss:

1
G = -D(G(z))

D_Loss:

1
D = D(G(z).detach()) - D(x)

因为公式是最大化$D(x) - D(G(z))$， 因此代码实现就是最小化$D(G(z)) - D(x)$

WGAN-GP

WGAN-GP中的一个重要的insight是：当函数满足$1-lipschitz$约束时， 函数的梯度范数处处等于1。

我们可以看到最后一项恒为正数， 若想最小化L， 那么$|\nabla_{\hat x}D(\hat x)|_2$趋向于1， 即函数的梯度范数趋向于1。

SNGAN

SNGAN的一个insight是：如果判决器的每一层都满足$1-Lipschitz$约束， 那么判决器满足$1-lipschitz$约束。

SNGAN的loss使用了hing loss

hinge loss

代码实现：

1
2
3
4
5
def hinge_loss(X, positive=True):
    if positive:
        return torch.relu(1-X).mean()
    else:
        return torch.relu(X+1).mean()

评价指标

Inception Score(IS)

生成质量

首先，将生成的图片$x$送入已经训练好的Inception模型（如Inception Net-V3）， 它是一个分类器 ， 会对每一个输入的图像输出一个1000维的标签向量$y$， 向量的每一维表示输入样本属于某个类别的概率。

熵是一种混乱程度的度量，对于质量较低的输入图像， 分类器无法给出明确的类别，其熵应比较大， 而对于质量越高的图像，其熵应当越小， 当$p(y \mid x)$为one-hot分布时，熵达到最小值0。

分布$p(y \mid x)$相对于类别的熵定义为：

其中，$p(y_i \mid x)$表示$x$属于第$i$类的概率， 计算方式如下图所示。

多样性

若GAN产生一批样本${x_1, x_2, …, x_n}$多样性比较好， 则标签向量${y_1, y_2, …, y_n}$的类别分布也应该是比较均匀的，也就是会所不同类别的概率基本上是相等的（假设训练样本的类别是均衡的）

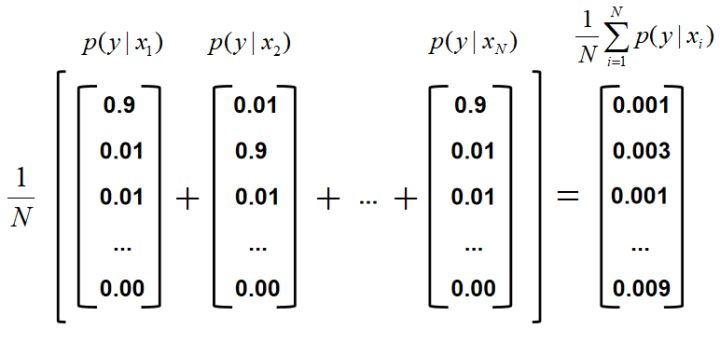
这里不太明白在这个N不确定的情况下，怎么算出等式右侧的结果的

又因为：

IS的缺陷

• 当GAN发生过拟合时，生成器只“记住了”训练集的样本，泛化性能差， 但IS无法检测到这个问题， 由于样本质量和多样性都比较好，IS仍然会很高
• 由于Inception Net-V3是在ImageNet上训练得到的， 故IS会偏爱ImageNet中的物体类别，而不是注重真实性。GAN生成的图片无论是如何逼真，只要它的类别不在ImageNet中，IS也会比较低。
• 若GAN生成类别的多样性足够，但是类内发生模式崩溃问题， IS无法探测。
• IS只考虑生成器的分布$p_g$而忽略数据集的分布$p_{data}$
• IS是一种伪度量
• IS的高低会收到图像像素的影响

Fréchet Inception Distance(FID)

分别把训练样本和生成器生成的样本送到分类器中（例如Inception Net-V3或者其他CNN等）， 抽取分类器的中间层的抽象特征，并假设该抽象特征符合多元高斯分布， 估计生成样本高斯分布的均值$\mu_g$和协方差$\sum_g$， 以及训练样本$\mu_{data}$和协方差$\sum_{data}$， 计算两个高斯分布的弗雷歇距离， 此距离即FID：

$\vec{I(y)}$

最后将FID作为评价指标。 示意图如下，其中虚线部分表示中间层

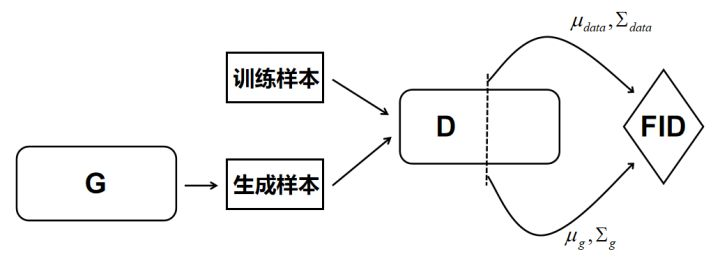
FID的数值越小，表示两个高斯分布越接近，GAN的性能越好。实践中发现，FID对噪声具有比较好的鲁棒性，能够对生成图像的质量有比较好的评价，其给出的分数与人类的视觉判断比较一致，并且FID的计算复杂度并不高，虽然FID只考虑的样本的一阶矩和二阶矩，但整体而言，FID还是比较有效的，其理论上的不足之处在于：高斯分布的简化假设在实际中并不成立。

余弦相似度

余弦相似度用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小。相比距离度量，余弦相似度更加注重两个向量在方向上的差异，而非距离或长度上。

余弦相似度可以用来度量两个人脸的身份向量的相似程度。 使用人脸识别网络提取出人脸图像的身份向量，计算其余弦相似度， 以度量两张人脸是否为同一人。

PSNR

峰值信噪比（Peak Signal to Noise Ratio，PSNR）经常用来评价图像质量。对于一张RGB三通道图像，其计算公式如下：

先计算图像与Ground Truth的均方误差MSE：

再计算PSNR：

普氏分析

PA（ 普氏分析）包含了常见的矩阵变换和SVD的分解过程，最终返回变换矩阵，调用变换矩阵，最后将原图和所求得矩阵放进warpAffine即可获的新图片。其中cv.warpAffine的功能就是根据变换矩阵对源矩阵进行变换。

点云匹配 PCL

Umeyama是一种PCL算法，简单点来理解就是将源点云(source cloud)变换到目标点云(target cloud)相同的坐标系下，包含了常见的矩阵变换和SVD的分解过程。最终返回变换矩阵。计算过程与普氏分析极其相似。

调用umeyama后获取变换所需的矩阵，最后将原图和所求得矩阵放进warpAffine即可获的新图片。

池化层

池化层的主要作用有三个：1. 增加CNN特征的平移不变性。2. 池化的降采样使得高层特征具有更大的感受野。 3. 池化的逐点操作相比卷积层的加权和更有利于优化求解。

实验证明1，3对性能的作用较小。以关键性较大的2来说： avg-pooling就是一般的平均滤波卷积操作，而max-pooling操作引入了非线性，可以用stride=2的CNN+RELU替代，性能基本能够保持一致，甚至稍好。已经有最新的一些网络结构去掉了pooling层用步长为2的卷积层代替。

可以参考这篇文献，有详细的实验对比：

Springenberg J T, Dosovitskiy A, Brox T, et al. Striving for simplicity: The all convolutional net[J]. arXiv preprint arXiv:1412.6806, 2014.

Reference

1. 机器学习笔记：张量、梯度、范数和图像分类
2. 内部协变量偏移(Internal Covariate Shift)和批归一化(Batch Normalization)
3. 视频换脸-Deepfakes代码解读和训练说明
4. 【CNN基础】常见的loss函数及其实现(一)——TV Loss
5. Total Variation
6. GAN评价指标最全汇总
7. 全面解析Inception Score原理及其局限性
8. Fréchet Inception Distance (FID)
9. 范数的理解。
10. 卷积神经网络中，步长为2的卷积层可以代替池化层吗？

• Previous
  【深度学习笔录】WGAN-GP论文阅读及其实现
• Next
  【深度学习笔录】AdaIN论文阅读及其实现