论文部分
Abstract
Gatys等人提出了一个神经算法, 它能给一个图片的内容以另一个图片的风格, 实现了所谓的风格迁移。 然而, 他们的框架需要一个缓慢的迭代优化过程, 这限制了它的实际应用性。 用前馈神经网络来快速地估计被提出来用于加速神经风格迁移。 不幸的是, 加速的同时也带来了代价:网络通常会固定在一种风格并且不能自适应任意的新风格。 在这篇文章中, 我们提出一个简单但是有效的方法第一次使得能够实时进行任意风格的迁移。我们方法的核心是一个全新的自适应的实例规范化层(AdaIN), 它将内容特征的均值和方差与样式特征的均值和方差对齐。我们的方法实现的速度可与现有最快方法相媲美,而不受限于一组预定义的样式。此外,我们的方法允许使用单个前馈神经网络灵活地进行用户控制,例如内容风格的平衡,风格插值,颜色和空间控制。
Introduction
Gatys的开创性工作展现了深度神经网络(DNN)不仅编码一张图片的内容,而且编码一张图片的风格。 而且, 图片的风格和内容是可分离的:保存一张图片的内容的同时改变它的风格是可能的。 这种风格迁移的方式足够灵活去结合内容和任意图片的风格。 然而, 它依赖于一个特别慢的优化过程。
很多人已经致力于加速神经风格的迁移。 他们尝试训练一个前馈神经网络, 它通过一个前馈过程展现出图片的风格。 大多数前馈网络的一个主要限制是每个网络受限于一种风格。 最近有很多工作解决了这个问题, 但是它们仍然首先与有限的风格集合, 或者比单风格迁移的方式慢很多。
在这片文章中, 我们提出了第一个神经风格迁移算法, 它解决了基础性的灵活性与速度难以权衡的窘境。我们的方法能够实时迁移任意种新的风格, 结合了优化模型的灵活性以及前馈方式饿的速度。 我们的方式收起发育实例规范化层(IN), 它在前馈风格迁移中十分有效。 为了解释实例规范化的成功,我们提出一种新的解释, 即实例规范化通过规范化特征数据来实现风格规范化, 它已经被发现带有图片的风格信息。 根据我们的解释, 我们为IN引入了一个简单的扩展,即自适应实例规范化(AdaIN)。给定一个内容输入和一个风格输入, AdaIN仅仅调整内容输入的均值和方差来匹配风格输入的均值和方差。 通过实验, 我们发现AdaIN通过迁移特征数据有效地结合了前者地内容和后者地风格。 然后,通过将AdaIN输出反相回到图像空间,解码器网络学习生成最终的风格化图像。
Related work
Style transfer: 样式转移的问题起源于非真实感的渲染,并且与纹理合成和迁移密切相关。一些早期的方法包括对线性滤波器响应进行直方图匹配和非参数采样。这些方法通常依赖于低级数据信息,并且通常无法捕获语义结构。Gatys等人第一次展示了印象深刻的风格迁移结果通过在一个深度神经网络的卷积层里匹配特征数据。最近,一些新的提升被提出。Li和Wand 在深层特征空间中引入了基于马尔可夫随机场(MRF)的框架来实施局部模式。Gatys等人提出的方式控制色彩保留, 空间位置, 以及风格迁移的规模。
Gatys等人的框架基于一个慢优化过程, 通过迭代更新图片以最小化通过一个损失网络计算出的一个内容损失和一个风格损失。即便在现代GPU上, 它也需要几分钟的时间来收敛。 因此,移动应用程序中的设备上处理太慢而无法实用。一个应变方法是用一个前馈神经网络来替换掉这个优化过程, 这个神经网络最小化同样的目标。这些前馈风格迁移方式三倍量级快于优化方式的风格迁移, 打开了实施应用的大门。 Wang等人用一个多分辨率结构提升了前馈风格迁移的粒度。Ulyanov等人提出的方式提升生成样本的质量和多样性。 然而, 上述的前馈方式有受限场景,因为每个网络只能有一种固定的风格。 为了解决这个问题, Dumoulin等人提出了一个网络能够编码32种风格以及它们的插值。 与我们的工作同时,Li等, 提出了一种前馈架构,可以合成多达300种纹理并迁移16种风格。但是, 以上两种方式不能适应在训练种没有见过的任意种风格。
最近, Chen和Schmidt 引入了一种前馈方法,该方法可以通过风格交换层来迁移任意风格。给定内容和风格图片的特征激活, 风格交换层通过patch-by-patch的方式将内容特征替换为最匹配的风格特征。不过, 他们的风格交换层创建了新的计算瓶颈:对于512x512输入的图片, 超过95%的计算花费在风格交换层上。我们的方式也允许任意风格的迁移,但是速度快于他们两个数量级。
另外一个关键问题是在风格迁移中使用什么样的风格损失函数。 Gatys的原始框架通过匹配特征激活之间的二阶数据来匹配样式, 由Gram矩阵捕获。其他有效的损失函数也被提出,如 MRF loss, adversarial loss, histogram loss, CORAL loss, MMD loss, 以及在通道级别的均值和方差的距离。注意到所有的损失函数目标都是在匹配风格图像和合成图像之间的特征数据。
Deep generative image modeling. 有几种图像生成的框架可供选择, 变分自编码器, auto-regressive模型, 以及生成对抗网络。 GAN已经取得了印象深刻的图像生成质量。 各种各样GAN的提升的框架被提出, 比如条件生成, 多阶段处理, 以及更好地训练目标函数。 GANs同样被应用于风格迁移和cross-domain图像生成。
Background
Batch Normalization
Ioffe和Szegedy等人的工作引入了一种批规范化层(Batch Normalization), 它通过规范化统计数据使前馈神经网络的训练变得容易。 BN层原始设计用来加速分类网络的训练, 但是发现它在生成模型中也同样有效。对于一个给定的输入$x \in R^{N \times C \times H \times W}$, BN层为每个特征通道规范化均值和标准差:
\[BN(x) = \gamma(\frac{x - \mu(x)}{\sigma(x)}) + \beta \tag 1\]其中$\gamma, \beta \in R^C$是从数据中学习到的仿射参数: $\mu(x), \sigma(x) \in R^C$是均值和标准差, 针对每个通道跨批大小维度和空间维度进行计算:
\[\mu_c(x) = \frac{1}{NHW}\sum_{n=1}^N \sum_{h=1}^H \sum_{w=1}^W x_{nchw} \tag 2\] \[\sigma_c (x) = \sqrt{\frac{1}{NHW}\sum_{n=1}^N \sum_{h=1}^H \sum_{w=1}^W (x_{nchw} - \mu_c(x))^2 + \epsilon} \tag 3\]BN在训练过程中使用小批量统计,并在推理过程中将其替换为普通的特征信息,从而在训练和推理之间引入差异。
Instance Normalization
在最初的前馈式风格化方式中,风格迁移网络在每个卷积层后包含一个BatchNorm层。惊喜的是, Ulyanov等人发现通过将BN层替换成IN层可以取得显著的提升。
\[IN(x) = \gamma(\frac{x - \mu(x)}{\sigma(x)}) + \beta \tag 4\]不同于BN层, 这里的$\mu(x)$和$\sigma(x)$分别针对每个通道和每个样本跨空间维度进行计算:
\[\mu_{nc}(x) = \frac{1}{HW}\sum_{h=1}^H \sum_{w=1}^W x_{nchw} \tag 5\] \[\sigma_{nc}(x) = \sqrt{\frac{1}{HW}\sum_{h=1}^H \sum_{w=1}^W (x_{nchw} - \mu_{nc}(x))^2 + \epsilon} \tag 6\]另外一个不同点是IN层在测试时仍然不变, 而BN层会去掉。
Conditional Instance Normalization
Dumoulin等人提出了一个条件实例规范化层, 它为每种风格s学习不同的参数$\gamma^s$和$\beta^s$的集合, 而不是学习一个仿射参数$\gamma$和$beta$的单个集合:
\[CIN(x; s) = \gamma^s(\frac{x - \mu(x)}{\sigma(x)}) + \beta^s \tag 7\]在训练期间, 一种风格图像和它的索引s随机地从一个固定的风格集合$s \in {1, 2, …, S}$(在他们的实验中S = 32)选出。内容图像被一个带有使用参数$\gamma^s$和$\beta^s$的CIN层的风格迁移网络处理。惊喜的是,使用相同的卷积但IN层中的仿射参数不同的网络可以生成完全不同样式的图像。
相比于一个不带有规范化层的网络, 一个带有CIN层的网络需要2FS额外的参数, 其中F是在网络中特征映射的总数量。因为额外参数的数量随着风格数量线性地扩大, 把他们的方式扩展成一个大量风格数量的模型是很有挑战性的。此外,他们的方式不能适应任意种新的风格,在没有重新训练的情况下。
Interpreting Instance Normalization
尽管(条件)实例规范化取得了巨大的成功, 但为什么它对风格迁移有效仍然难以捉摸。Ulyanov等人将IN的成功归因于内容图片的对比度的不变性。 然而, IN发生在特征空间中,因此它比像素空间中的简单对比度规范化具有更深远的影响。也许更令人惊讶的是,IN中的仿射参数可以完全改变输出图像的风格。
我们已经知道深度神经网络的卷积特征数据能够捕获一个图片的风格。 当Gatys等人使用二级特征数据作为他们的优化目标, Li等人最近展现了匹配更多其他的数据, 包括通道级别的均值和方差, 并且对风格迁移十分有效。 受这些观察启发, 我们认为实例规范化通过规范化特征参数, 也就是均值和方差, 表现出一种风格规范化的形式。尽管深度神经网络被用作一个图像描述子, 我们认为生成网络的特征数据能够控制生成图像的风格。
我们运行improved texture networks的代码去实现一个单风格转换, 使用IN或者BN层。 不出所料, 使用IN的模型收敛快于使用BN的模型(Fig.1(a))。 为了测试在improved texture networks的解释,我们通过在亮度通道上执行直方图均衡化,将所有训练图像标准化为相同的对比度。如Fig.1(b)所示, IN仍然有效, 表明improved texture networks的解释不完整。 为了验证我们的假设, 我们使用一个预训练的风格迁移网络规范化所有训练的图片为同样的风格(但不同与目标风格)。根据Fig.1(c), 当图像已经进行风格规范化化时,IN带来的改进变得很小。两者之间存在的差距表明这个预训练网络的风格规范化并不完美。同时, 使用BN的模型在已经风格规范化的图像上可以像使用了IN的模型在原始图像上收敛地一样快。我们的结果表明IN确实执行了一种风格规范化。
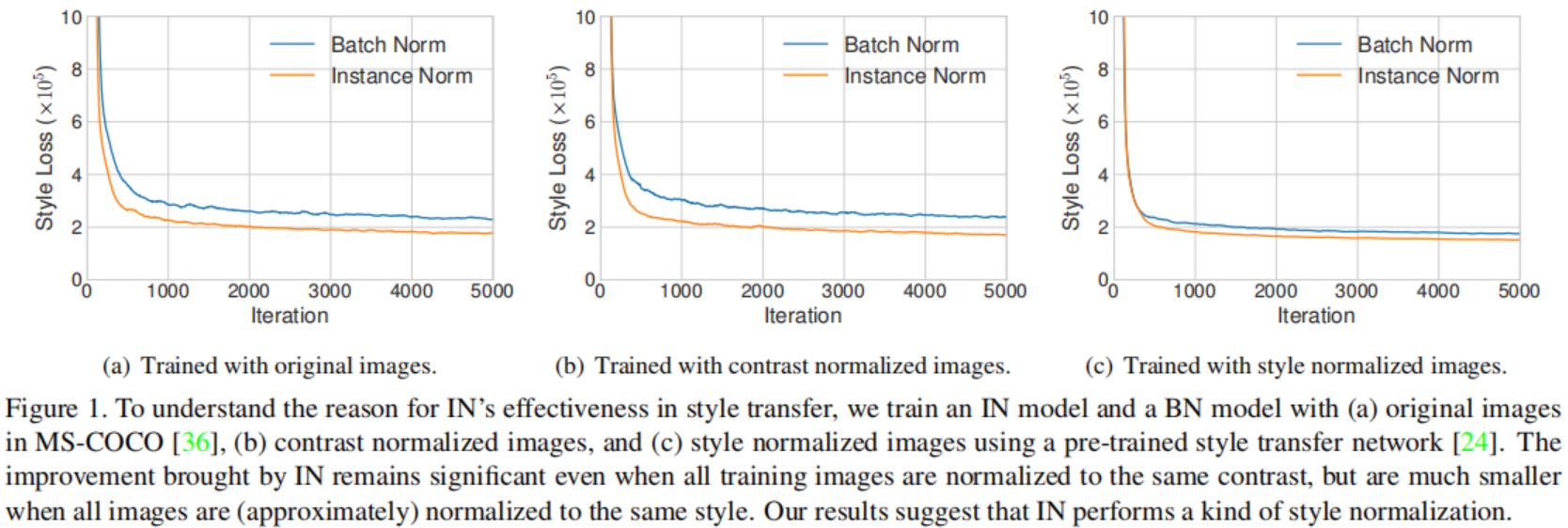
因为BN规范化了一个批量样本的统计数据而不是单个样本的统计数据, 它可以直观地理解为以单个样本风格为中心将一批样本规范化。然而,对于每个样本,可能仍然有着不同的风格。这是我们不想要的结果,当我们想要迁移所有的图像为同一种风格时, 就像原始前馈风格迁移算法情况一样。尽管卷积层可能学会去补偿批次之间的风格差异, 它给训练带来了额外的负担。IN层能够将每个样本的风格规范化为目标风格,相当于抛弃了原始的风格信息, 网络的剩余部分能够专注于内容的控制, 因此能够加速训练。CIN的成功原因也变得清晰:不同的仿射参数能够规范化特征数据为不同的值, 因此规范化输出图像为不同的风格。
Adaptive Instance Normalization
如果IN通过仿射参数规范化输入维单中指定风格, 那么它能不能使用自适应的仿射参数适应任意种给定风格呢?这里,我们提出了一种IN的简单拓展, 我们称之为自适应实例规范化(AdaIN)。AdaIN接受一个内容输入x和一个风格输入y, 然后仅仅将x通道级别的均值和方差对齐匹配成y的均值和方差。不像BN, IN或者CIN, AdaIN没有可学习的仿射参数。 相反,它自适应地计算仿射参数通过风格输入:
\[AdaIN(x, y) = \sigma(y)(\frac{x - \mu(x)}{\sigma(x)}) + \mu(y) \tag 8\]这里我们仅仅用$\sigma(y)$放缩了规范化的内容输入, 并且用$\mu(y)$偏置了它。与IN相似, 这些数据信息是跨空间位置计算的。
直观地,让我们考虑一个特征通道, 该通道可以检测特定风格的笔触。 带有这种笔触的风格图片可以对这种特征产生一个高平均的激活。由AdaIN产生的输出将对这种特征具有相同的高平均激活。 使用一个前馈解码器可以使这个笔触特征返回图像空间。 这种特征通道的方差可以编码更多微小的风格信息, 这些信息也能迁移到AdaIN的输出,最终输出图像。
简而言之, AdaIN通过迁移数据特征, 尤其是通道级别的均值和方差, 在特征空间执行风格迁移。我们的AdaIN层扮演了了像风格交换层相似的角色。 当风格交换操作是非常耗时和耗内存, 我们的AdaIN层像IN层一样简单, 几乎没有增加计算成本。
Experimental Setup
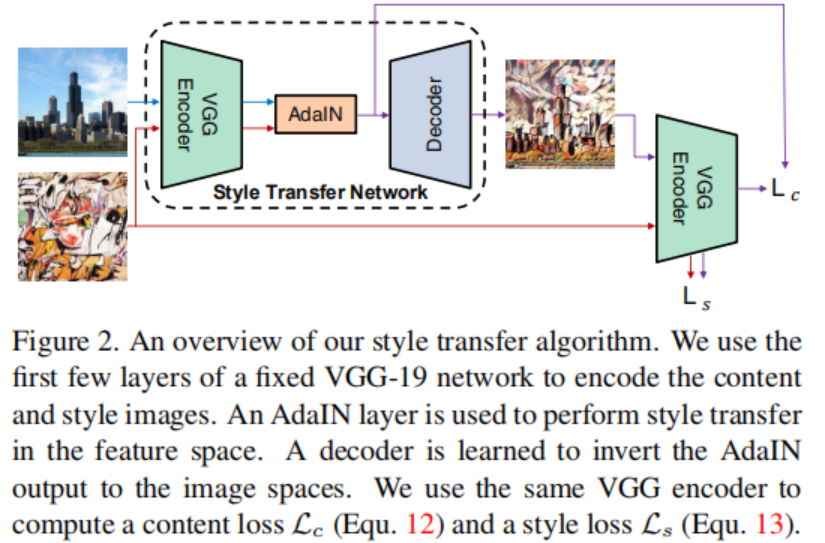
Fig.2 展示了一个基于AdaIN层我们的风格迁移网络的概览。
Architecture
我们的风格迁移网络T将内容图像c和任意风格图像s作为输入,然后合成了一个输出图像, 这个图像结合了前者的内容和后者的风格。 我们采用了一个简单的编码器-解码器结构, 其中编码器f是一个固定了前几层(到relu4_1)的预训练过的VGG19。在特征空间内容图像和风格图像的编码之后, 我们把两者的特征映射都送入AdaIN层, 它将内容特征映射的均值和方差对齐风格特征映射的均值和方差, 产生一个目标特征映射t:
\[t = AdaIN(f(c), f(s)) \tag 9\]一个随机初始化的编码器g训练将t映射到图像空间, 生成风格化的图像T(c, s):
\[T(c, s) = g(t) \tag {10}\]解码器大多数镜像解码器, 所有池化层均被最近的上采样取代,以减少棋盘效应。我们在f和g中都使用了反射填充,以避免出现边界伪像。另外一个重要的结构选择是是否解码器应该使用实例规范化、批规范化或者没有规范化层。如第四部分讨论, IN规范化每个样本到一种单风格, 而BN规范化一批样本为单风格为中心。 两者都不是我们想要的, 当我们想让编码器生成具有大量不同风格的图像。因此我们不在解码器中使用规范化层。
Training
我们训练我们的网络使用MS-COCO作为内容图像并且收集自WikiArt的油画数据集作为风格图像。每个数据集包含了大概80000个训练样本。 我们使用adam优化器并且batchsize为8内容-风格图像对。在训练期间,我们首先将两个图像的小维度拉伸到512, 在保留比例的前提下, 然后随机裁剪256x256的区域。 因为我们的网络是全卷积, 在测试时他能够被用于任意尺寸的图像。
我们使用预训练的VGG19来计算损失函数去训练解码器:
\[L = L_c + \lambda L_s \tag {11}\]它是用风格损失权重$\lambda$结合了内容损失$L_c$和风格损失$L_s$。内容损失是目标特征和输出图像的特征两者之间的欧几里得距离。我们使用AdaIN的输出t作为内容目标, 而不是通常那样使用内容图像的特征。 我们发现这会导致更快的收敛速度和对齐我们反向AdaIN输出t的目标。
\[L_c = \|f(g(t)) - t \|_2 \tag {12}\]因为我们的AdaIN层仅仅迁移了风格特征的均值和方差, 我们的风格损失函数匹配这些数据。尽管我们发现通常使用的Gram矩阵损失可以产生相似的结果, 我们匹配IN的数据因为从概念上讲它更干净。Li等人也探索了这种风格损失函数:
\[L_s = \sum_{i=1}^L \|\mu(\phi_i(g(t))) - \mu(\phi_i(s))\|_2 + \sum_{i=1}^L \|\sigma(\phi_i(g(t))) - \sigma(\phi_i(s))\|_2 \tag {13}\]其中每个$\phi_i$表示VGG19中用来计算风格损失的层。 在我们的实验中我们以相同的权重使用 $relu1_1, relu2_1, relu3_1, relu4_1$层。
实现部分
引入相关包
1
2
3
4
5
6
7
8
import torch.nn as nn
import argparse
from pathlib import Path
from PIL import Image
from torchvision import transforms
from torchvision.utils import save_image
计算均值方差
1
2
3
4
5
6
7
8
9
def calc_mean_std(feat, eps=1e-5):
# eps is a small value added to the variance to avoid divide-by-zero.
size = feat.size()
assert (len(size) == 4)
N, C = size[:2]
feat_var = feat.view(N, C, -1).var(dim=2) + eps
feat_std = feat_var.sqrt().view(N, C, 1, 1)
feat_mean = feat.view(N, C, -1).mean(dim=2).view(N, C, 1, 1)
return feat_mean, feat_std
AdaIN
1
2
3
4
5
6
7
8
9
def adaptive_instance_normalization(content_feat, style_feat):
assert (content_feat.size()[:2] == style_feat.size()[:2])
size = content_feat.size()
style_mean, style_std = calc_mean_std(style_feat)
content_mean, content_std = calc_mean_std(content_feat)
normalized_feat = (content_feat - content_mean.expand(
size)) / content_std.expand(size)
return normalized_feat * style_std.expand(size) + style_mean.expand(size)
Decoder
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
decoder = nn.Sequential(
nn.ReflectionPad2d((1, 1, 1, 1)),
nn.Conv2d(512, 256, (3, 3)),
nn.ReLU(),
nn.Upsample(scale_factor=2, mode='nearest'),
nn.ReflectionPad2d((1, 1, 1, 1)),
nn.Conv2d(256, 256, (3, 3)),
nn.ReLU(),
nn.ReflectionPad2d((1, 1, 1, 1)),
nn.Conv2d(256, 256, (3, 3)),
nn.ReLU(),
nn.ReflectionPad2d((1, 1, 1, 1)),
nn.Conv2d(256, 256, (3, 3)),
nn.ReLU(),
nn.ReflectionPad2d((1, 1, 1, 1)),
nn.Conv2d(256, 128, (3, 3)),
nn.ReLU(),
nn.Upsample(scale_factor=2, mode='nearest'),
nn.ReflectionPad2d((1, 1, 1, 1)),
nn.Conv2d(128, 128, (3, 3)),
nn.ReLU(),
nn.ReflectionPad2d((1, 1, 1, 1)),
nn.Conv2d(128, 64, (3, 3)),
nn.ReLU(),
nn.Upsample(scale_factor=2, mode='nearest'),
nn.ReflectionPad2d((1, 1, 1, 1)),
nn.Conv2d(64, 64, (3, 3)),
nn.ReLU(),
nn.ReflectionPad2d((1, 1, 1, 1)),
nn.Conv2d(64, 3, (3, 3)),
权重下载链接:
https://drive.google.com/open?id=108uza-dsmwvbW2zv-G73jtVcMU_2Nb7Y
VGG
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
vgg = nn.Sequential(
nn.Conv2d(3, 3, (1, 1)),
nn.ReflectionPad2d((1, 1, 1, 1)),
nn.Conv2d(3, 64, (3, 3)),
nn.ReLU(), # relu1-1
nn.ReflectionPad2d((1, 1, 1, 1)),
nn.Conv2d(64, 64, (3, 3)),
nn.ReLU(), # relu1-2
nn.MaxPool2d((2, 2), (2, 2), (0, 0), ceil_mode=True),
nn.ReflectionPad2d((1, 1, 1, 1)),
nn.Conv2d(64, 128, (3, 3)),
nn.ReLU(), # relu2-1
nn.ReflectionPad2d((1, 1, 1, 1)),
nn.Conv2d(128, 128, (3, 3)),
nn.ReLU(), # relu2-2
nn.MaxPool2d((2, 2), (2, 2), (0, 0), ceil_mode=True),
nn.ReflectionPad2d((1, 1, 1, 1)),
nn.Conv2d(128, 256, (3, 3)),
nn.ReLU(), # relu3-1
nn.ReflectionPad2d((1, 1, 1, 1)),
nn.Conv2d(256, 256, (3, 3)),
nn.ReLU(), # relu3-2
nn.ReflectionPad2d((1, 1, 1, 1)),
nn.Conv2d(256, 256, (3, 3)),
nn.ReLU(), # relu3-3
nn.ReflectionPad2d((1, 1, 1, 1)),
nn.Conv2d(256, 256, (3, 3)),
nn.ReLU(), # relu3-4
nn.MaxPool2d((2, 2), (2, 2), (0, 0), ceil_mode=True),
nn.ReflectionPad2d((1, 1, 1, 1)),
nn.Conv2d(256, 512, (3, 3)),
nn.ReLU(), # relu4-1, this is the last layer used
nn.ReflectionPad2d((1, 1, 1, 1)),
nn.Conv2d(512, 512, (3, 3)),
nn.ReLU(), # relu4-2
nn.ReflectionPad2d((1, 1, 1, 1)),
nn.Conv2d(512, 512, (3, 3)),
nn.ReLU(), # relu4-3
nn.ReflectionPad2d((1, 1, 1, 1)),
nn.Conv2d(512, 512, (3, 3)),
nn.ReLU(), # relu4-4
nn.MaxPool2d((2, 2), (2, 2), (0, 0), ceil_mode=True),
nn.ReflectionPad2d((1, 1, 1, 1)),
nn.Conv2d(512, 512, (3, 3)),
nn.ReLU(), # relu5-1
nn.ReflectionPad2d((1, 1, 1, 1)),
nn.Conv2d(512, 512, (3, 3)),
nn.ReLU(), # relu5-2
nn.ReflectionPad2d((1, 1, 1, 1)),
nn.Conv2d(512, 512, (3, 3)),
nn.ReLU(), # relu5-3
nn.ReflectionPad2d((1, 1, 1, 1)),
nn.Conv2d(512, 512, (3, 3)),
nn.ReLU() # relu5-4
)
权重下载链接:
https://drive.google.com/open?id=1w9r1NoYnn7tql1VYG3qDUzkbIks24RBQ
loss Net
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
class Net(nn.Module):
def __init__(self, encoder, decoder):
super(Net, self).__init__()
enc_layers = list(encoder.children())
# *list[:]返回的是迭代器一串的内容
self.enc_1 = nn.Sequential(*enc_layers[:4]) # input -> relu1_1
self.enc_2 = nn.Sequential(*enc_layers[4:11]) # relu1_1 -> relu2_1
self.enc_3 = nn.Sequential(*enc_layers[11:18]) # relu2_1 -> relu3_1
self.enc_4 = nn.Sequential(*enc_layers[18:31]) # relu3_1 -> relu4_1
self.decoder = decoder
self.mse_loss = nn.MSELoss()
# fix the encoder
for name in ['enc_1', 'enc_2', 'enc_3', 'enc_4']:
for param in getattr(self, name).parameters():
param.requires_grad = False
# extract relu1_1, relu2_1, relu3_1, relu4_1 from input image
def encode_with_intermediate(self, input):
results = [input]
for i in range(4):
func = getattr(self, 'enc_{:d}'.format(i + 1))
# enc_1(input)->enc_2(enc_1(input))->...
# 存储了input和各层的输出结果
results.append(func(results[-1]))
# 返回各层输出
return results[1:]
# extract relu4_1 from input image
def encode(self, input):
for i in range(4):
input = getattr(self, 'enc_{:d}'.format(i + 1))(input)
return input
def calc_content_loss(self, input, target):
assert (input.size() == target.size())
assert (target.requires_grad is False)
return self.mse_loss(input, target)
def calc_style_loss(self, input, target):
assert (input.size() == target.size())
assert (target.requires_grad is False)
input_mean, input_std = calc_mean_std(input)
target_mean, target_std = calc_mean_std(target)
return self.mse_loss(input_mean, target_mean) + \
self.mse_loss(input_std, target_std)
def forward(self, content, style, alpha=1.0):
assert 0 <= alpha <= 1
style_feats = self.encode_with_intermediate(style)
content_feat = self.encode(content)
t = adain(content_feat, style_feats[-1])
# 这里和faceshifter的80%类似, 为什么这么做?
t = alpha * t + (1 - alpha) * content_feat
g_t = self.decoder(t)
g_t_feats = self.encode_with_intermediate(g_t)
loss_c = self.calc_content_loss(g_t_feats[-1], t)
loss_s = self.calc_style_loss(g_t_feats[0], style_feats[0])
for i in range(1, 4):
# i = [1,4)
loss_s += self.calc_style_loss(g_t_feats[i], style_feats[i])
return loss_c, loss_s
在预测中并没有用到
图片预处理
1
2
3
4
5
6
7
8
9
def test_transform(size, crop):
transform_list = []
if size != 0:
transform_list.append(transforms.Resize(size))
if crop:
transform_list.append(transforms.CenterCrop(size))
transform_list.append(transforms.ToTensor())
transform = transforms.Compose(transform_list)
return transform
风格迁移
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def style_transfer(vgg, decoder, content, style, alpha=1.0,
interpolation_weights=None):
assert (0.0 <= alpha <= 1.0)
# 这里是 5block VGG 出来的feature?
# 在下面的代码中只是用了前32层,这里是以参数形式传入
content_f = vgg(content)
style_f = vgg(style)
# 什么是interpolation_weights?
if interpolation_weights:
_, C, H, W = content_f.size()
feat = torch.FloatTensor(1, C, H, W).zero_().to(device)
base_feat = adaptive_instance_normalization(content_f, style_f)
for i, w in enumerate(interpolation_weights):
feat = feat + w * base_feat[i:i + 1]
content_f = content_f[0:1]
else:
# 送入AdaIN的不是应该是4_1层之后的feature吗?
feat = adaptive_instance_normalization(content_f, style_f)
feat = feat * alpha + content_f * (1 - alpha)
return decoder(feat)
相关参数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
parser = argparse.ArgumentParser()
# Basic options
parser.add_argument('--content', type=str, default='./content.jpg',
help='File path to the content image')
parser.add_argument('--style', type=str, default='./style.jpg',
help='File path to the style image, or multiple style \
images separated by commas if you want to do style \
interpolation or spatial control')
parser.add_argument('--vgg', type=str, default='./vgg_normalised.pth')
parser.add_argument('--decoder', type=str, default='./decoder.pth')
# Additional options
parser.add_argument('--content_size', type=tuple, default=(512, 512),
help='New (minimum) size for the content image, \
keeping the original size if set to 0')
parser.add_argument('--style_size', type=tuple, default=(512, 512),
help='New (minimum) size for the style image, \
keeping the original size if set to 0')
parser.add_argument('--crop', action='store_true', default=False,
help='do center crop to create squared image')
parser.add_argument('--save_ext', default='.jpg',
help='The extension name of the output image')
parser.add_argument('--output', type=str, default='./',
help='Directory to save the output image(s)')
# Advanced options
parser.add_argument('--preserve_color', action='store_true', default=False,
help='If specified, preserve color of the content image')
parser.add_argument('--alpha', type=float, default=1.0,
help='The weight that controls the degree of \
stylization. Should be between 0 and 1')
parser.add_argument(
'--style_interpolation_weights', type=str, default='',
help='The weight for blending the style of multiple style images')
args = parser.parse_known_args()[0]
相关初始化
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
do_interpolation = False
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
output_dir = Path(args.output)
content_paths = [Path(args.content)]
style_paths = [Path(args.style)]
decoder.eval()
vgg.eval()
decoder.load_state_dict(torch.load(args.decoder))
vgg.load_state_dict(torch.load(args.vgg))
vgg = nn.Sequential(*list(vgg.children())[:31])
vgg.to(device)
decoder.to(device)
content_tf = test_transform(args.content_size, args.crop)
style_tf = test_transform(args.style_size, args.crop)
预测
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
for content_path in content_paths:
if do_interpolation: # one content image, N style image
style = torch.stack([style_tf(Image.open(str(p))) for p in style_paths])
content = content_tf(Image.open(str(content_path))) \
.unsqueeze(0).expand_as(style)
style = style.to(device)
content = content.to(device)
with torch.no_grad():
output = style_transfer(vgg, decoder, content, style,
args.alpha, interpolation_weights)
output = output.cpu()
output_name = output_dir / '{:s}_interpolation{:s}'.format(
content_path.stem, args.save_ext)
save_image(output, str(output_name))
else: # process one content and one style
for style_path in style_paths:
content = content_tf(Image.open(str(content_path)))
style = style_tf(Image.open(str(style_path)))
# if args.preserve_color:
# style = coral(style, content)
style = style.to(device).unsqueeze(0)
content = content.to(device).unsqueeze(0)
with torch.no_grad():
output = style_transfer(vgg, decoder, content, style,
args.alpha)
output = output.cpu()
output_name = output_dir / '{:s}_stylized_{:s}{:s}'.format(
content_path.stem, style_path.stem, args.save_ext)
save_image(output, str(output_name))
实验结果
风格图片:

内容图片:

迁移图片:

Reference
- Huang X, Belongie S. Arbitrary style transfer in real-time with adaptive instance normalization[C]//Proceedings of the IEEE International Conference on Computer Vision. 2017: 1501-1510.
- naoto0804/pytorch-AdaIN