公式推导
用$\pi_\theta(s)$表示一个参数为$\theta$的网络,也就是一个actor
$S_i$表示observation, $a_i$表示action, $r_i$表示reward
总共的reward: $R_\theta = \sum_{t=1}^{T}r_t$
即便是使用同一个actor, $R_\theta$每次也是不同的
一场游戏(episode)表示为$\tau$
- \[\tau = \{s_1, a_1, r_1, s_2, a_2, r_2, ... , s_T, a_T, r_T\}\]
- \[R(\tau) = \sum_{n=1}^{N}r_n\]
如果我们使用一个actor玩游戏,每个$\tau$有一个被采样的概率
- 概率依赖于actor的参数$\theta$: $P(\tau \mid \theta)$
使用$\pi_\theta$玩游戏N次, 得到\(\{\tau_1, \tau_2, ..., \tau_N\}\), 相当于从$P(\tau \mid \theta)$采样 $\tau$ N次
因此
\[\bar R_\theta = \sum_\tau R(\tau)P(\tau \mid \theta) \approx \frac{1}{N} \sum_{n=1}^{N} R(\tau^n)\]问题状态:
\[\theta^* = arg \max_\theta \bar R_\theta, \quad \bar R_\theta = \sum_\tau R(\tau)P(\tau \mid \theta)\]梯度下降:
- 从$\theta^0$开始
- $\theta^1 \leftarrow \theta^0 + \eta \nabla \bar R_{\theta^0}$
- $\theta^2 \leftarrow \theta^1 + \eta \nabla \bar R_{\theta^1}$
- …
因此$R(\tau)$可以是不可微的
\[\nabla \bar R_{\theta} = \sum_\tau R(\tau) \nabla P(\tau \mid \theta) = \sum_\tau R(\tau)P(\tau \mid \theta) \frac{\nabla P(\tau \mid \theta)}{P(\tau \mid \theta)} \\ = \sum_\tau R(\tau)P(\tau \mid \theta) \nabla log P(\tau \mid \theta)\]因为
\[\frac{dlog(f(x))}{dx} = \frac{1}{f(x)}\frac{df(x)}{dx}\]使用$\pi_\theta$玩游戏N次, 得到\(\{\tau^1, \tau^2, ..., \tau^N\}\)
\[\sum_\tau R(\tau)P(\tau \mid \theta) \nabla log P(\tau \mid \theta) = \frac{1}{N}\sum_{n=1}^{N} R(\tau^n)\nabla log P(\tau^n \mid \theta)\] \[\tau = \{s_1, a_1, r_1, s_2, a_2, r_2, ..., s_T, a_T, r_T\}\] \[P(\tau \mid \theta) = p(s_1)p(a_1 \mid s_1, \theta)p(r_1, s_2 \mid s_1, a_1)p(a_2 \mid s_2, \theta)p(r_2, s_3 \mid s_2, a_2)...\] \[P(\tau \mid \theta) = p(s_1) \prod p(a_t \mid s_t, \theta)p(r_t, s_{t+1} \mid s_t, a_t)\] \[log P(\tau \mid \theta) = log p(s_1) + \sum_{t=1}^{T}(log p(a_t \mid s_t, \theta) + log p(r_t, s_{t+1} \mid s_t, a_t))\]忽略掉不含$\theta$的项:
\[\nabla P(\tau \mid \theta) = \sum_{t=1}^{T} \nabla log p(a_t \mid s_t, \theta)\] \[\theta^{new} \leftarrow \theta^{old} + \eta \nabla \bar R_{\theta^{old}}\] \[\nabla \bar R_\theta \approx \frac{1}{N} \sum_{n=1}^{N} R(\tau^n) \nabla log P(\tau^n \mid \theta) = \frac{1}{N} \sum_{n=1}^{N} R(\tau^n) \sum_{t=1}^{T_n}\nabla log p(a_t^n \mid s_t^n, \theta) \\ = \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_n} R(\tau^n) \nabla log p(a_t^n \mid s_t^n, \theta)\]为什么要取log?
因为:
\[\nabla log p(a_t^n \mid s_t^n, \theta) = \frac{\nabla p(a_t^n \mid s_t^n, \theta)}{p(a_t^n \mid s_t^n, \theta)}\]相当于根据概率对梯度做了一个Normalization。
如果在$\tau^n$时, 机器在$s_t^n$时采用了$a_t^n$:
- $R(\tau^n)$是正的, 微调$\theta$减小$p(a_t^n \mid s_t^n)$
- $R(\tau^n)$是负的, 微小$\theta$增大$p(a_t^n \mid s_t^n)$
$R(\tau^n)$可能会永远都是正的
在理想情况下, a、b、c三个action根据概率增减
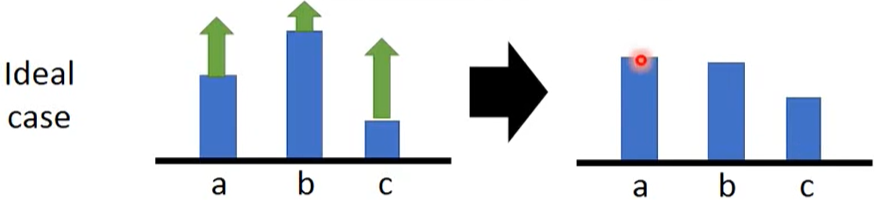
实际情况下, 可能采样不到三个action
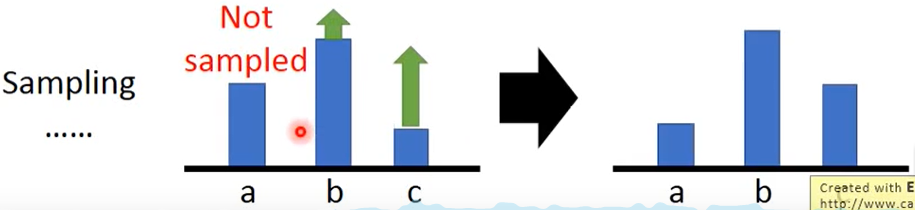
这个时候,未被采样到的action概率将会下降
解决方法,自己设计一个bias:
\[\nabla \bar R_\theta \approx \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_n}(R(\tau^n) - b) \nabla log p(a_t^n \mid s_t^n, \theta)\]如果$R(\tau^n)$比bias这个baseline大,那么action的概率才会增加,如果$R(\tau^n)$比bias小,那么action的概率还是会减小。
mark: Rainbow
Proximal Policy Optimization(PPO)
From on-policy to off-policy
以下棋为例:
on-policy: 自己下自己学
off-policy:在旁边看别人下