马尔科夫的属性

未来仅和当前有关，而与过去无关。

一个state $S_t$ 是马尔科夫， 当且仅当

\[P[S_{t+1} \mid S_t] = P[S_{t+1} \mid S_1, ..., S_t]\]

对于一个马尔科夫状态$s$和下一状态$s’$， 状态转移概率定义为：

\[P_{ss'} = P[S_{t+1} = s' \mid S_t = s]\]

状态转移矩阵$P$定义为所有的状态$s$到所有的下一状态$s’$的转移概率：

\[P = from \quad \begin{matrix} to \\ \left[\begin{array}{rr} p_{11} & ... & p_{1n} \\ ... \\ p_{n1} & ... & p_{nn} \end{array}\right] \end{matrix}\]

马尔科夫过程

马尔科夫过程是无记忆性的随机过程。

马尔科夫过程（马尔科夫链）是一个tuple $(S, P)$

• $S$是一个有限的状态集合
• $P$是状态转义概率矩阵， $P_{ss’} = P[S_{t+1} = s’ \mid S_t = s]$

Markov Reward Process(MRP)

Markov reward process是一个有value的马尔科夫链

一个Markov Reward Process是一个tuple$(S, P, R, \gamma)$

• $S$是有限状态集
• $P$是状态转移概率矩阵, $P_{ss’} = P[S_{t+1} = s’ \mid S_t = s]$
• $R$是reward函数， $R_s = E[R_{t+1} \mid S_t = s]$
• $\gamma$是系数， $\gamma \in [0, 1]$

返回的$G_t$是所有奖励乘以系数的和

\[G_t = R_{t+1} + \gamma R_{t+2} + ... = \sum_{k=0}^\infty \gamma^k R_{t + k + 1}\]

为什么是这样的一个公式呢，因为某一状态，我们可以产生多种可能的状态序列， 那么不同的序列就会计算出不同的$G_t$

注意：计算$G_t$和概率无关

Value函数

value函数 $v(s)$ 给定状态$s$长期的value

定义：

一个MRP的状态value函数$v(s)$应该从状态$s$开始返回：

\[v(s) = E[G_t \mid S_t = s]\]

此时看起来 各状态的value函数仅和$\gamma$和reward有关， 与状态转移概率无关。

MRPs的贝尔曼等式(Bellman Equation for MRPs)

value函数可以被分解为两部分：

• 立即的reward $R_{t+1}$
• 带权重的下一状态的value $\gamma v(S_{t+1})$

\[v(s) = E[G_t \mid S_t = s] \\ = E[R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + ... \mid S_t = s] \\ = E[R_{t+1} + \gamma (R_{t+2} + \gamma R_{t+3} + ...) \mid S_t = s] \\ = E[R_{t+1} + \gamma G_{t+1} \mid S_t = s] \\ = E[R_{t+1} + \gamma v(S_{t+1}) \mid S_t = s]\]

贝尔曼方程可被表示为：

\[v = R + \gamma Pv\]

其中$v$是进入每个状态的value列向量

\[\begin{matrix}\ \left[\begin{array}{ccc} v(1) \\ \vdots \\ v(n) \end{array}\right] = \left[\begin{array}{ccc} R_1 \\ \vdots\\ R_n \end{array}\right] + \gamma \left[\begin{array}{ccc} P_{11} & \cdots & P_{1n}\\ \vdots \\ P_{n1} & \cdots & P_{nn} \end{array}\right] \left[\begin{array}{ccc} v(1) \\ \vdots \\ v(n) \end{array}\right] \end{matrix}\]

贝尔曼等式是一个线性等式

它可以这样求解

\[v = R + \gamma P v\] \[(1 - \gamma P) v = R\] \[v = (1 - \gamma P)^{-1} R\]

对n个状态计算的时间复杂度为$O(n^3)$

只能对小规模的MRPs直接求解

对大规模的MRPs， 有以下的迭代方法求解：

• 动态规划(Dynamic Programming)
• 蒙特卡罗估计(Monte-Carlo evaluation)
• Temperal-Difference learning

马尔科夫决策过程(Markov Decision Process)

马尔科夫决策过程是一个tuple $(S, A, P, R, \gamma)$

• $S$是有限状态集
• $A$是有限动作集
• $P$是转移概率矩阵， $P_{ss’}^a = P[S_{t+1} = s’ \mid S_t = s, A_t = a]$
• $R$睡觉哦reward函数， $R_s^a = E[R_{t+1} \mid S_t = s, A_t = a]$
• $\gamma$是折扣系数， $\gamma \in [0, 1]$

policy $\pi$ 定义为给定states对actions的分布

\[\pi(a \mid s) = P[A_t = a \mid S_t = s]\]

policy定义为一个智能体的所有行为。

MDPs的 policies 取决于于现在的状态(不是历史状态)

• 给定一个MDP $M = (S, A, P, R, \gamma)$和一个policy $\pi$
• 状态序列$S_1, S_2, …$是一个马尔科夫过程$(S, P^\pi)$
• state和reward序列 $S_1, R_2, S_2, …$是一个Markov Reward Process $（S, P^\pi, R^\pi, \gamma）$
• 其中

\[P_{s, s'}^\pi = \sum_{a \in A} \pi(a \mid s) P_{s, s'}^a\] \[R_s^\pi = \sum_{a \in A} \pi(a \mid s) R_s^a\]

stae-value函数可以被分解为立即的reward加上下一state的折扣后的value。

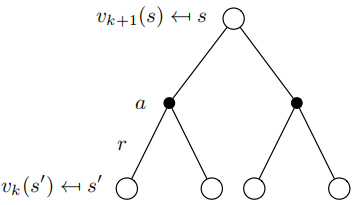
\[v_\pi(s) = E_\pi[R_{t+1} + \gamma v_\pi(S_{t+1}) \mid S_t = s]\]

action-value函数相似地可以被分解。

\[q_\pi (s, a) = E_\pi [R_{t+1} + \gamma q_\pi(S_{t+1}, A_{t+1}) \mid S_t = s, A_t = a]\]

$v$表示特定的state有多好， $q$表示采取特定的action之后有多好

$v_\pi(s)$和$q_\pi(s, a)$的关系

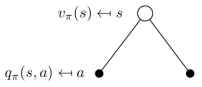
在遵循策略$\pi$时，状态$s$的价值体现在该状态下遵循某一策略而采取的所有可能行为的价值按行为发生的概率的乘积的和

\[v_\pi(s) = \sum_{a \in A} \pi(a \mid s) q_\pi(s, a)\]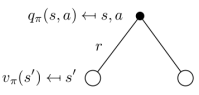

某一状态下采取一个行为的价值，可以分为两部分：一是离开这个状态的价值， 二是所有进入新的状态的价值与其转移概率乘积的和

\[q_\pi (s, a) = R_s^a + \gamma \sum_{s' \in S} P_{ss'}^a v_\pi(s')\]

Optimal Value Function

最优的 state-value 函数 $v_\pi(s)$ 是对所有policies最大化value函数：

\[v_\pi(s) = \max_\pi v_\pi(s)\]

最优的action-value函数$q_\pi(s, a)$是对所有的policies最大化 action-value函数：

\[q_\pi(s, a) = \max_\pi q_\pi (s, a)\]

Optimal Policy

对policies定义一个偏序：

\[\pi \geq \pi' \quad if \quad v_\pi(s) \geq v_{\pi'}(s), \forall s\]

对于所有的马尔科夫决策过程：

• 存在一个最优policy $\pi_$， 它和其他的policies相等或者比其他policies更好， $\pi_ \geq \pi, \quad \forall \pi$
• 所有的最优policies取得最优的value函数， $v_{\pi_}(s) = v_(s)$
• 所有的最优policies取得最优的action-value函数， $q_{\pi_}(s, a) = q_(s, a)$

$v_*$的贝尔曼最优方程

最优的value函数由贝尔曼最优方程递归地决定

\[v_*(s) = \max_a q_* (s, a)\]

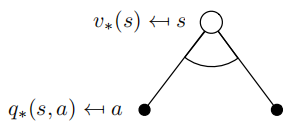
$Q^*$的贝尔曼最优方程

\[q_*(s, a) = R_s^a + \gamma \sum_{s' \in S}P_{ss'}^a v_*(s')\]

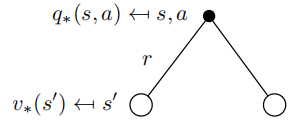
联立上面两式：

\[v_*(s) = \max_a R_s^a + \gamma \sum_{s' \in S} P_{ss'}^a v_*(s')\]

同样可以得到：

\[q_*(s, a) = R_s^a + \gamma \sum_{s' \in S} P_{ss'}^a \max_a q_*(s', a')\]

MRP和MDP的区别

MRP等于时小船随波逐流

MDP等于有个人在划船

蒙特卡罗算法计算MRP

首先$i \leftarrow 0$， $G_t \leftarrow 0$

当 $i \neq N$时：

• 从状态$s$和时间$t$产生一段episode（一局游戏）
• 使用产生的episode计算return $g = \sum_{i=t}^{H-1} \gamma^{i-t}r_i$
• 令 $G_t \leftarrow G_t + g, i \leftarrow i + 1$

最终$V_t(s) \leftarrow G_t / N$

动态规划计算MRP

对于所有的状态$s \in S$， $V’(s) \leftarrow 0, V(s) \leftarrow \infty$

当 $| V - V’ | > \epsilon$时：

• $V \leftarrow V’$
• 对于所有的状态$s \in S$， $V’(s) = R(s) + \gamma \sum_{s’\in S}P(s’ \mid s)V(s’)$

对所有的$s \in S$， 返回$V’(s)$

动态规划的属性

最佳的子结构

• 最佳适用原则
• 最优解可以被分解为多个子问题

重叠的子问题

• 子问题重复递归很多次
• 解决方案可以缓存并且复用

马尔科夫决策过程满足两个属性

• 贝尔曼方程给出递归的分解
• Value函数存储并复用解决方案

动态规划假设已经知道了MDP的所有信息

它用来在MDP中做一个计划

对于预测：

• 输入： MDP$(S, A, P, R, \gamma)$ 和 policy $\pi$， 或者 MRP$(S, P^\pi, R^\pi, \gamma)$
• 输出：value函数$v_\pi$

对于控制：

• 输入： MDP$(S, A, P, R, \gamma)$
• 输出： 最优value函数$v_$ 以及 最优的policy $\pi_$

Policy evaluation on MDP

目标： 评估一个给定的MDP的policy $\pi$

输出： 在policy $\pi$下的价值函数$v^\pi$

解决方案： 在Bellman expectation backup上迭代

算法： Synchronous backup

• 在每次迭代 t+1, 对所有的state $s \in S$， 从$v_t(s’)$更新$v_{t+1}(s)$， 其中$s’$是$s$的一个下一状态 \(v_{t+1}(s) = \sum_{a \in A} \pi(a \mid s)(R(s, a) + \gamma \sum_{s' \in S}P(s' \mid s, a)v_t(s'))\)

收敛： $v_1 \rightarrow v_2 \rightarrow … \rightarrow v^\pi$

Policy评估(Policy Evaluation， 也叫prediction)

问题：评价一个policy $\pi$

解决方法： iterative application of Bellman expectation backup

使用同步备份：

• 对每次迭代k+1
• 对所有状态 $s \in S$
• 从 $v_k(s’)$ 更新 $v_{k+1}(s)$\
• 其中 $s’$ 是 $s$ 的下一状态

\[v_{k+1} = \sum_{a \in A} \pi(a \mid s) (R_s^a + \gamma \sum_{s' \in S} P_{ss'}^a v_k(s'))\] \[v^{k+1} = R^\pi + \gamma P^\pi v^k\]

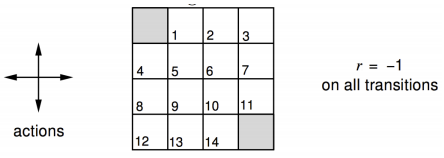
• 无折扣的MDP($\gamma = 1$)
• 非终结状态 1, …, 14
• 一个终结状态(灰色隐形， 图中出现两次)
• 离开网格的 action 保持 state 不变
• 直到终结状态达到， Reward是-1
• agent 服从均匀分布 policy， $\pi(n \mid ·) = \pi(e \mid ·) = \pi(s \mid ·) = \pi(w \mid ·) = 0.25$

最优化原则

一个policy $\pi(a \mid s)$从状态$s$得到最优的value， $v_\pi(s) = v_*(s)$， 当且仅当

• 从$s$可以到达任意的$s’$
• $\pi$从状态$s’$取得最优value， $v_\pi(s’) = v_*(s’)$

如果我们知道方案的子问题$v_*(s’)$

然后解决方案$v_*(s)$可以通过向前一步得到：

\[v_*(s) \leftarrow \max_{a \in A} R_s^a + \gamma \sum_{s' \in S} P_{ss'}^a v_*(s')\]

value iteration是指使用它们迭代更新

最优化价值函数

最优化的state-value函数$v^*(s)$是对所有的policies最大化价值函数：

\[v^*(s) = \max_\pi v^\pi(s)\]

最优的policy

\[\pi^*(s) = \mathop{argmax}_\pi v^\pi(s)\]

当我们知道最优的价值时，一个MDP就被解决了

存在一个最优的价值函数， 但可能是多个最优策略（两个actions都有最优的价值函数）

寻找最佳的policy

一个最佳的policy可以通过最大化$q^*(s, a)$得到

\[\pi^*(a \mid s) = \begin{cases} 1, \quad if \quad a = argmax_{a \in A} q^*(s, a) \\ 0, \quad otherwise \end{cases}\]

对任意的MDP总存在一个确定地最优策略

如果我们知道$q^*(s, a)$， 我们立即可以得到最优策略

MDP Control

计算最优策略

\[\pi^*(s) = \mathop{argmax}_\pi v^\pi(s)\]

最优策略对于一个MDP是一个有限范围问题(agent永远行动)：

• 确定的
• 静止的（不依赖于时间）
• 多种state-actions得到确定的最优价值

通过policy iteration提升一个策略

通过两步进行迭代：

• 评估策略$\pi$（给定当前$\pi$计算$v$）
• 分别对$v^\pi$通过贪心算法提升策略

\[\pi' = greedy(v^\pi)\]

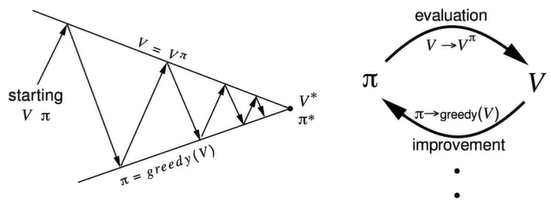
Policy Improvement

计算策略$\pi$的state-action value:

\[q^{\pi_i}(s, a) = R(s, a) + \gamma \sum_{s' \in S} P(s' \mid s, a) v^{\pi_i}(s')\]

对所有的$s \in S$计算新的policy $\pi_{i+1}$

\[\pi_{i+1}(s) = \mathop{argmax}_a q^{\pi_i}(s, a)\]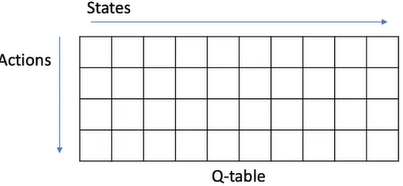

形象地描述q函数， 对不同的action和state可以形成一张q table， 在其中找出最大的q价值。

Monotonic Improvement in Policy（Policy的单调递增）

考虑一个确定地policy， $a = \pi(s)$

我们可以通过贪心算法提升policy

\[\pi'(s) = \mathop{argmax}_{a \in A} q_\pi(s, a)\]

一步对于任意的状态$s$提升value

\[q_\pi(s, \pi'(s)) = \max_{a \in A} q_\pi(s, a) \geq q_\pi(s, \pi(s)) = v_\pi(s)\]

因此它提升value函数， $v_{\pi’}(s) \geq v_\pi(s)$

\[v_\pi(s) \leq q_\pi(s, \pi'(s)) = E_{\pi'}[R_{t+1} + \gamma v_\pi(S_{t+1}) \mid S_t = s] \\ \leq E_{\pi'}[R_{t+1} + \gamma q_{\pi}(S_{t+1}, \pi'(S_{t+1})) \mid S_t = s] \\ \leq E_{\pi'}[R_{t+1} + \gamma R_{t+2} + \gamma^2 q_\pi(S_{t+2}, \pi'(S_{t+2})) \mid S_t = s] \\ \leq E_{\pi'}[R_{t+1} + \gamma R_{t+2} + ... \mid S_t = s] = v_{\pi'}(s)\]

如果提升停止

\[q_\pi(s, \pi'(s) = \max_{a \in A} q_\pi (s, a) = q_\pi (s, \pi(s)) = v_\pi(s)\]

贝尔曼最优方程满足

\[v_\pi(s) = \max_{a \in A} q_\pi(s, a)\]

因此对于所有的$s \in S$， $v_\pi(s) = v_*(s)$是最优策略

贝尔曼最优化方程

最优的价值函数通过贝尔曼最优化方程得到：

\[v^*(s) = \max_a q^*(s, a)\] \[q^*(s, a) = R(s, a) + \gamma \sum_{s' \in S} P(s' \mid s, a) v^*(s')\]

因此

\[v^*(s) = \max_a R(s, a) + \gamma \sum_{s' \in S} P(s' \mid s, a)v^*(s')\] \[q^*(s, a) = R(s, a) + \gamma \sum_{s \in S} P(s' \mid s, a) \max_{a'}q^*(s', a')\]

Value Iteration 通过将贝尔曼最优化函数作为更新规则

如果我们知道解决方案的子问题 $v^*(s’)$,， 它是最优的

然后最优的$v^*(s)$可以通过对下面的Bellman Optimality backup rule找到解

\[v(s) \leftarrow \max_{a \in A}(R(s, a) + \gamma \sum_{s' \in S}P(s' \mid s, a)v(s'))\]

value iteration就是迭代地应用这些更新

Value Iteration的算法

目标： 找到最优的policy $\pi$

解决方案： 通过Bellman optimality backup迭代

Value Iteration 算法：

• 对所有的状态$s$， 初始化 $k=1$和 $v_0(s) = 0$
• 对于 $k=1 : H$， 对于每个状态$s$

\[q_{k+1}(s, a) = R(s, a) + \gamma \sum_{s' \in S}P(s' \mid s, a)v_k(s')\] \[v_{k+1}(s) = \max_a q_{k+1}(s, a)\]

• 在value Iteration之后找到最优的policy

\[\pi(s) = \mathop{argmax}_a R(s, a) + \gamma \sum_{s' \in S} P(s' \mid s, a) v_{k+1}(s')\]

Policy Iteration和Value Iteration的对比

Policy Iteration包括： Policy evaluation + policy improvement， 重复它们两个知道policy收敛

Value Iteration包括： 找到最优的value function + 一个policy extraction。 不需要重复它们，因为一旦value function是最优的，那么policy也应该是最优的。

找到最优的value fuction也可看作policy improvement和删减的policy evaluation的结合。

Reference

1. 《强化学习》第二讲 马尔科夫决策过程
2. 强化学习纲要 第二课 马尔科夫决策过程 上

---

• Previous
  【强化学习】强化学习相关概念
• Next
  【强化学习】强化学习环境相关

---