Model-free Prediction
估计未知MDP的价值函数
什么叫已知的MDP:
- R和P都暴露给智能体
- 因此可以使用policy iteration和value iteration
Policy iteration
给定一个已知的MDP, 计算最优的策略和最优的价值函数
Policy evaluation:在Bellman expectation backup上迭代:
\[v_i(s) = \sum_{a \in A} \pi(a \mid s) (R(s, a) + \gamma \sum_{s' \in S} P(s' \mid s, a) v_{i-1}(s'))\]上面在做的事情就是 将所有可能的action得到的价值按概率求和, 也就是求期望。
Policy improvement: 对action-value function q使用贪心算法
\[q_{\pi_i}(s, a) = R(s, a) + \gamma \sum_{s' \in S} P(s' \mid s, a) v_{\pi_i}(s')\] \[\pi_{i+1}(s) = \mathop{argmax}_a q_{\pi_i}(s, a)\]上面在座的事情就是: 将policy evaluation中求和的每项找出最大的
Value iteration
给定一个已知的MDP, 计算最优的价值函数
在Bellman optimality backup上迭代:
\[v_{i+1} \leftarrow \max_{a \in A} R(s, a) + \gamma \sum_{s' \in S} P(s' \mid s, a) v_i(s')\]在Value Iteration之后检索最优策略
\[\pi^*(s) \leftarrow \mathop{arg max}_a R(s, a) + \gamma \sum_{s' \in S} P(s' \mid s, a) v_{end}(s')\]Model-free RL: Learning by interaction
Model-free RL 能够通过和环境交互解决问题
不再直接地获取已知的动态转移和奖励函数
trajectories/episode 由智能体和环境交互收集
每个trajectory/episode 包含 \(\{S_1, A_1, R_1, S_2, A_2, R_2, ..., S_T, A_T, R_T\}\)
如果我们没有获取MDP模型,估计一个特定策略的期望回报:
- Monte Caolo policy evaluation
- Temporal Difference(TD) learning
Monte Carlo Policy Evaluation
Return: 在policy$\pi$下, $G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + …$
$v^\pi(s) = E_{r \thicksim \pi}[G_t \mid s_t = s]$, 因此期望是由$\pi$产生的所有trajectories $\tau$
MC simulation: 我们可以仅仅采样很多的trajectories, 计算所有trajectory的实际回报, 然后平均它们
MC policy evaluation 使用均值回报替代期望回报
MC不需要MDP dynamics/rewards, 没有bootstrapping, 并且没有假设state是马尔科夫
仅应用于episodic MDPs(每个episode终结)
为了评估state $v(s)$
- 每个时间步骤$t$状态$s$在一个episode被访问
- 叠加计数器: $N(s) \leftarrow N(s) + 1$
- 叠加总回报: $S(s) \leftarrow S(s) + G_t$
- Value通过均值回报估计: $v(s) = S(s) / N(s)$
通过大数定律, $v(s) \rightarrow v^\pi(s)$ , 当$N(s) \rightarrow \infty$
叠加均值(Incremental mean)
均值通过样本平均$x_1, x_2, …$计算:
\[\mu_t = \frac{1}{t} \sum_{j=1}^t x_j \\ = \frac{1}{t}(x_t + \sum_{j=1}^{t-1}x_j) \\ = \frac{1}{t}(x_t + (t - 1)\mu_{t-1}) \\ = \mu_{t-1} + \frac{1}{t}(x_t - \mu_{t-1})\]Incremental MC Updates
收集一个episode $(S_1, A_1, R_1, …, S_t)$
对于每个状态 $s_t$ 计算回报 $G_t$
\[N(S_t) \leftarrow N(S_t) + 1\] \[v(S_t) \leftarrow v(S_t) + \frac{1}{N(S_t)}(G_t - v(S_t))\]或者使用running mean。 很好地解决非静止的问题:
\[v(S_t) \leftarrow v(S_t) + \alpha (G_t - v(S_t))\]什么是running mean?
如果在计算之前,你不清楚有多少数据,且数据是一个一个获得, 此时计算的平均值称之为running_mean, 这样的计算场景称之为online。
策略评估中DP和MC的区别
动态规划(DP)
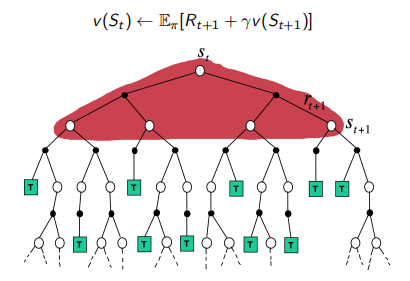
动态规划(DP)通过由$v_{i-1}$估计的价值 bootstrapping得到其余的期望回报计算$v_i$
bootstrapping的意思是 估计一个量是根据之前计算的一个量来估计的。
在Bellman expectatiob backup上迭代:
\[v_i(s) \leftarrow \sum_{a \in A} \pi(a \mid s) (R(s, a) + \gamma \sum_{s' \in S} P(s' \mid s, a) v_{i-1}(s'))\]蒙特卡罗(MC)
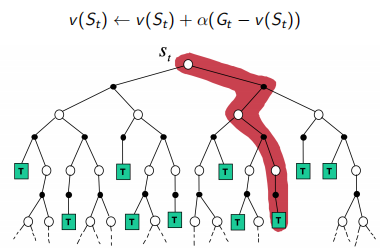
MC通过一个采样的episode更新期望回报
\[v(S_t) \leftarrow v(S_t) + \alpha (G_{i, t} - v(S_t))\]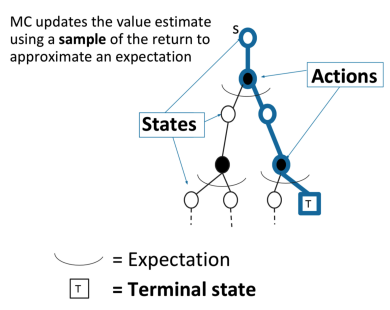
MC相对DP的优势
MC可以工作在环境未知的情况下
即便完全了解环境的动态时, 使用采样episode工作仍然巨大的优势。 例如, 转移概率复杂到难以计算。
计算单个状态价值的成本独立于状态的总数量。 因此我们可以从感兴趣的状态开始采样episodes, 然后平均回报。
Temporal-Difference(TD)Learning
TD方法从经历的episodes中直接学习
TD是model-free的: 无 MDP 转移/奖励 的知识
TD从不完整的episodes中通过bootstrapping学习
目标: 在策略$pi$下从经历中在线学习$v_\pi$
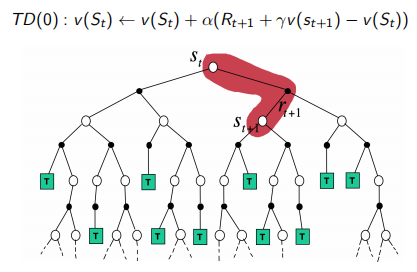
最简单的TD算法: TD(0)
- 通过估计回报$R_{t+1} + \gamma v(S_{t+1})$更新$v(S_t)$
- \[v(S_t) \leftarrow v(S_t) + \alpha(R_{t+1} + \gamma v(S_{t+1}) - v(S_t))\]
$R_{t+1} + \gamma v(S_{t+1})$被叫做TD target
$\delta_t = R_{t+1} + \gamma v(S_{t+1}) - v(S_t)$被叫做TD error
比较: 增量式的Monte-Carlo
- 给定一个episode $i$, 通过真实的回报 $G_t$ 更新 $v(S_t)$
- \[v(S_t) \leftarrow v(S_t) + \alpha (G_{i, t} - v(S_t))\]
TD相对MC的优势
TD更新价值估计 使用$s_{t+1}$的采样 去估计一个期望
TD更新价值估计通过bootstrapping, 使用$V(s_{t+1})$估计
MC更新价值估计 使用一个回报的采样 去估计一个期望
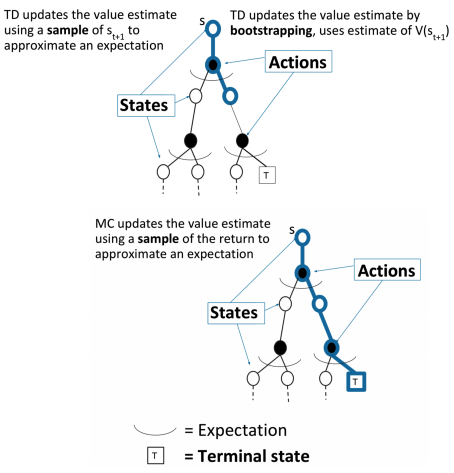
TD和MC的比较
TD能够在每一步后在线学习
MC在回报已知前必须等待至episode的结束
TD可以从不完整的序列中学习
MC只能从完成的序列中学习
TD工作在连续的(非终结的)环境
MC仅工作在episodic(终结的)的环境
TD利用了马尔科夫属性, 在马尔科夫环境中更有效
MC没有使用马尔科夫属性, 在非马尔科夫环境中更有效
n-step TD
n-step TD 方法可以推广位 one-step TD 和 MC
我们可以从1到移动到其他的一个特定任务所需的数
对于$n = 1, 2, \infty$, 考虑下面的 n-step 回报:
\[n=1(TD) \quad G_t^{(1)} = R_{t+1} + \gamma v(S_{t+1})\] \[n=2 \quad G_t^{(2)} = R_{t+1} + \gamma R_{t+2} + \gamma^2 v(S_{t+2})\] \[n = \infty(MC) \quad G_t^{\infty} = R_{t+1} + \gamma R_{t+2} + ... + \gamma^{T-t-1} R_T\]因此 n-step 回报可以定义为:
\[G_t^n = R_{t+1} + \gamma R_{t+2} + ... + \gamma^{n-1} R_{t+n} + \gamma^n v(S_{t+n})\]n-step TD:
\[v(S_t) \leftarrow v(S_t) + \alpha(G_t^n - v(S_t))\]对于DP、MC和TD的Bootstrapping和Sampling
Bootstrapping: 一次估计一次更新
- MC没有bootstrap
- DP有bootstrap
- TD有bootstrap
Sampling: 采样一次期望更新一次
- MC 采样
- DP不采样
- TD采样
Model-free Control
最优化未知MDP的价值函数
Policy Iteration
通过两步迭代:
- 评估策略$\pi$(给定当前$\pi$, 计算$v$)
- 分别对$v_\pi$使用贪心算法提升策略
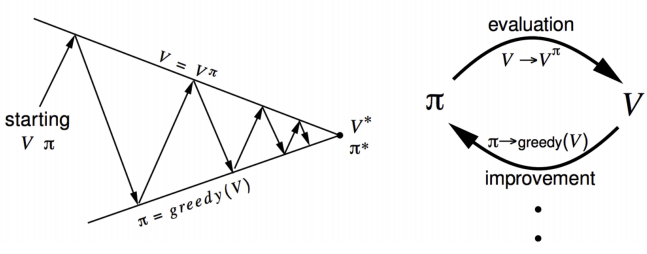
已知MDP的Policy Iteration
这是一个动态规划(DP)方法的Policy Iteration
计算一个策略$\pi$的state-action value:
\[q_{\pi_i}(s, a) = R(s, a) + \gamma \sum_{s' \in S} P(s' \mid s, a) v_{\pi_i}(s')\]对所有的$s \in S$计算新的策略$\pi_{i+1}$有:
\[\pi_{i+1}(s) = \mathop{argmax}_a q_{\pi_i}(s, a)\]问题:如果没有$R_{s, a}$和$P(s’ \mid s, a)$应该怎么做?
使用Action-Value函数的广义Policy Iteration
这是一个使用蒙特卡洛方法的Policy Iteration
策略评估: 蒙特卡罗策略评估: $Q = q_\pi$
策略提升: 通过贪心策略改进它
\[\pi(s) = \mathop{argmax}_a q(s, a)\]探索开始的蒙特卡罗(Monte Carlo ES(Exploring Starts))
能够保证$\pi$收敛的一个假设是: episode有探索的开始
探索的开始可以保证所有的action被无限地选择
初始化:
- 对于所有的$s \in S$, $\pi(s) \in A(s)$(任意地)
- 对于所有的$s \in S, a \in A(s)$, $Q(s, a) \in R$(任意地)
- 对于所有的$s \in S, a \in A(s)$, $Returns(s, a) \leftarrow$ empty list
无限循环(对于每一个episode):
- 当概率大于0时,随机地选择$S_0 \in S, A_0 \in A(S_0)$
- 在策略$\pi$下, 从$S_0, A_0$产生一段episode: $S_0, A_0, R_1, …, S_{T-1}, A_{T-1}, R_T$, $G \leftarrow 0$
- $t = T-1, T-2, …, 0$, episode的每步循环:
$G \leftarrow \gamma G + R_{t+1}$
除非在$S_0, A_0, S_1, A_1, …, S_{t-1}, A_{t-1}$中出现$S_t, A_t$
添加$G$到$Returns(S_t, A_t)$
$Q(S_t, A_t) \leftarrow average(Returns(S_t, A_t))$
$\pi(S_t) \leftarrow \mathop{argmax}_a Q(S_t, a)$
$\epsilon$-Greedy 探索的蒙特卡罗
权衡探索和发掘
$epsilon$-Greedy 探索: 确保连续的探索
- 所有的action以一个非零的概率尝试
- 以 $1 - \epsilon$ 的概率选择贪心策略的action
- 以概率$\epsilon$随机地选择action
策略提升理论: 对于任意的$\epsilon$-greedy策略$\pi$, $\epsilon$-greedy策略$\pi’$关于$q_\pi$是一种改进, $v_{\pi’} \geq v_{\pi}(s)$
\[q(s, \pi'(s)) = \sum_{a \in A} \pi'(a \mid s) q_\pi(s, a) \\ = \frac{\epsilon}{\mid A \mid} \sum_{a \in A} q_\pi(s, a) + (1 - \epsilon) \max_a q_\pi(s, a) \\ \geq \frac{\epsilon}{\mid A \mid} \sum_{a \in A} q_\pi(s, a) + (1 - \epsilon) \sum_{a \in A} \frac{\pi(a \mid s) - \frac{\epsilon}{\mid A \mid}}{1 - \epsilon} q_\pi(s, a) \\ = \sum_{a \in A} \pi(a \mid s) q_\pi(s, a) = v_\pi(s)\]因此, $v_{\pi’}(s) \geq v_\pi(s)$
算法:

MC和TDPrediction和Control
Temporal-difference(TD)learning相较于Monte-Carlo(MC)有几个优势:
- Lower variance
- Online
- 可以是不完整的序列
因此在我们的控制循环中可以使用TD替代MC:
- 将TD应用于$Q(S, A)$
- 使用$\epsilon-greedy$策略提升
- 每个time-step更新, 而不是一个episode的最后更新
回忆 TD Prediction
一个epsiode由几个state和state-action对的变化的序列组成:
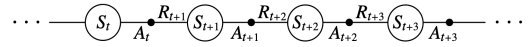
TD(0)方法用于估计value function V(S)
\[A_t \leftarrow 给定\pi, 为S找到action\] \[采用action \quad A_t, 观察 R_{t+1} 和 S_{t+1}\] \[V(S_t) \leftarrow V(S_t) + \alpha [R_{t+1} + \gamma V(S_{t+1} - V(S_t))]\]