两类重要的随机过程
到达过程: 新的“成功”和“到达”不依赖与该过程过去的历史情况。
马尔科夫过程: 未来的情况会依赖于过去的情况, 并且能够在某种程度上通过过去发生的情况去预测未来。
离散时间的马尔科夫链
离散的马尔科夫链有三个核心概念点: 离散时间、状态空间、转移概率。
在离散时间的马尔科夫链中,通常使用$n$来表示时刻, 用$S_n$来表示马尔科夫链在此时的状态, 那么马尔科夫链所有的状态会构成一个集合$S = {S_1, …, S_m}$, 这个$S$我们把它称作是离散时间马尔科夫链的状态空间。
当离散时间的马尔科夫链当前的状态时$i$时, 下一个状态等于$j$的概率就是转移概率, 记作$p_{ij}$。
转移概率$p_{ij}$本质上用一个条件概率就可以表达:
\[p_{ij} = P(X_{n+1}=j \mid X_n = i), i, j \in S\]举一个拥有三个状态的离散的马尔科夫链例子:
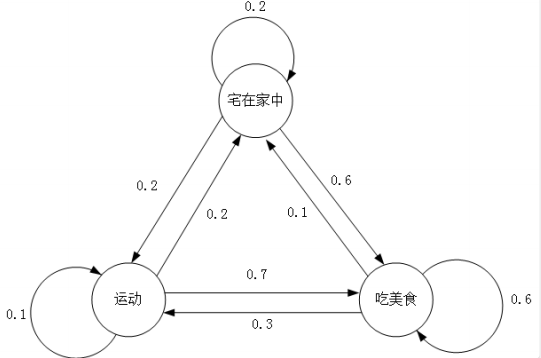
马尔科夫性(markov property)
只要时刻$n$的马尔科夫链的状态为$i$, 那么无论过去发生了什么, 也不论马尔科夫链是如何到达状态$i$的, 下一个时刻$n+1$转移到状态$j$的概率一定都是转移概率$p_{ij}$。
比如张三今天是在吃美食, 那么不管他昨天是在运动还是宅在家中, 他明天出去运动的概率都不变。
用条件概率表示:
\[P(X_{n+1} = j \mid X_n=i, X_{n-1}=i_{n-1}, ..., X_0 = i_0) = P(X_{n+1}=j \mid X_n = i) = p_{ij}\]转移概率矩阵
状态转移概率$p_{ij}$满足的性质:
- $p_{ij}$满足非负性
- $\sum_{j=1}^{m}p_{ij} = 1$
在状态空间$S$中,任意两个状态$i$和$j$之间都有一个转移概率$p_{ij}$, 并且满足$p_{ij} \geq 0$(当状态$i$无法转移到状态$j$的时候, $p_{ij}=0$)。那么我们可以把状态空间中状态间的所有转移概率按照顺序组成一个二维矩阵。
\[\begin{matrix} \left[\begin{array}{rr} p_{11} & p_{12} & \cdots & p_{1m} \\ p_{21} & p_{22} & \cdots & p_{2m} \\ \cdots & \cdots & \cdots & \cdots \\ p_{m1} & p_{m2} & \cdots & p_{mm} \end{array}\right] \end{matrix}\]一步到达与多步转移
多步转移写成条件概率的形式就是:
\[p^m(i, j) = P(X_{n+m} = j \mid X_n = i)\]例子
社会学中有一个非常著名的反映社会阶层流动的马尔科夫链, 在这个马尔科夫链的状态空间中, 有三个状态, 状态1是处于贫困水平,状态2是中产阶级, 状态3是财富自由, 它的状态转移矩阵为:
\[\begin{matrix} \left[\begin{array}{rr} 0.7 & 0.2 & 0.1 \\ 0.3 & 0.5 & 0.2 \\ 0.2 & 0.4 & 0.4 \end{array}\right] \end{matrix}\]假设爷爷处于贫困水平(状态1), 那么父亲处于中产阶级(状态2), 而你处于财富自由(状态3)的概率有多大?
从条件概率表达式入手:
\[P(X_2 = 3, X_1 = 2 \mid X_0 = 1) \\ = \frac{P(X_2 = 3, X_1 = 2, X_0 = 1)}{P(X_0 = 1)} \\ =\frac{P(X_2 = 3, X_1 = 2, X_0 = 1)}{P(X_1 = 2, X_0 = 1)} \times \frac{P(X_1 = 2, X_0 = 1)}{P(X_0 = 1)} \\ = P(X=2 \mid X_1 = 2, X_0 = 1) \times P(X_1 = 2 \mid X_0 =1)\]由于这是一个马尔科夫链, 因此满足:
\[P(X_2 = 3 \mid X_1 = 2, X_0 = 1) = P(X_2 = 3 \mid X_1 = 2)\]因此就有:
\[P(X_2 = 3, X_1 = 2 \mid X_0 = 1) = P(X_2 = 3\mid X_1 = 2)P(X_1 = 2 \mid X_0 = 1)\]因此这个问题的答案就是:
\[p_{12} p_{23} = 0.2 \times 0.2 = 0.04\]那么我们不指定父亲的状态,假设爷爷是贫困水平(状态1), 问孙子处于财富自由(状态3)的概率有多大?
\[P(X_2 = 3 \mid X_0 = 1) = P(X_2 = 3, X_1 = 1 \mid X_0 = 1) \\ + P(X_2 = 3, X_1 = 2 \mid X_0 = 1) \\ + P(X_2 = 3, X_1 = 3 \mid X_0 = 1) \\ = p_{11}p_{13} + p_{12}p_{23} + p_{13}p_{33} \\ = \sum_{k=1}^3 p_{1k}p_{k3} = 0.7 \times 0.1 + 0.2 \times 0.2 + 0.1 \times 0.4 \\ = 0.15\]多步转移与矩阵乘法
我们重点看上面这个式子:
\[P(X_2 = 3 \mid X_0 = 1) = p_{11}p_{13} + p_{12}p_{23} + p_{13}p_{33}\]转移矩阵
\[\begin{matrix} \left[\begin{array}{rr} 0.7 & 0.2 & 0.1 \\ 0.3 & 0.5 & 0.2 \\ 0.2 & 0.4 & 0.4 \end{array}\right] \end{matrix}\]上面的式子就是转移矩阵第一行和第三列点乘的结果。
如果我们讲转移概率矩阵与自身相乘, 也就是求它的二次幂, 即:
\[\begin{matrix} \left[\begin{array}{rr} 0.7 & 0.2 & 0.1 \\ 0.3 & 0.5 & 0.2 \\ 0.2 & 0.4 & 0.4 \end{array}\right]^2 = \\ \left[\begin{array}{rr} 0.7 & 0.2 & 0.1 \\ 0.3 & 0.5 & 0.2 \\ 0.2 & 0.4 & 0.4 \end{array}\right] \left[\begin{array}{rr} 0.7 & 0.2 & 0.1 \\ 0.3 & 0.5 & 0.2 \\ 0.2 & 0.4 & 0.4 \end{array}\right] \end{matrix}\]那么得到的新的$3 \times 3$二维矩阵里就包含了所有状态间, 通过两步到达的概率值。
路径概率问题
由$n$步转移概率所派生出来的路径概率问题。
给定一个马尔科夫链模型,我们可以计算未来任何一个给定状态序列的概率, 特别地:
\[P(X_0 = i_0, X_1 = i_1, ..., X_n = i_n) = P(X_0 = i_0)p_{i_0i_1}p_{i_1i_2}...p_{i_{n-1}i_n}\]首先由贝叶斯定理:
\[P(X_0 = i_0, X_1 = i_1, ..., X_n = i_n) = \\ P(X_n = i_n \mid X_0 = i_0, ..., X_{n-1} = i_{n-1})P(X_0 = i_0, ..., X_{n-1}=i_{n-1})\]依据马尔科夫性:
\[P(X_n = i_n \mid X_0 = i_0, ..., X_{n-1} = i_{n-1}) = P(X_n = i_n \mid X_{n-1} = i_{n-1}) = p_{i_{n-1}i_n}\]从而有:
\[p(X_0 = i_0, X_1 = i_1, ..., X_n = i_n) = p_{i_{n-1}i_n}P(X_0 = i_0, ..., X_{n-1}=i_{n-1})\]然后不断地递推就能够得到最开始的
\[P(X_0 = i_0, X_1 = i_1, ..., X_n = i_n) = P(X_0=i_0)p_{i_0i_1}p_{i_1i_2}...p_{i_{n-1}i_n}\]比如从你的太爷爷开始,太爷爷是贫穷,爷爷是贫穷, 爸爸是中产, 你是财富自由, 你儿子中产, 你孙子贫穷, 这就是一个典型的努力拼搏最后又富不过三代的悲剧路径。
那么路径的概率是:
\[P(X_0 = 1)p_{11}p_{12}p_{23}p_{32}p_{21}\]最左边的$P(X_0 = 1)$表示太爷爷是贫穷的概率,这个值定了,整个路径的概率就可以计算出来了。