马尔科夫链的稳态于采样的关系
马尔科夫链的稳态: 无论起始状态如何, 在状态转移矩阵P的作用下, 经过足够大的n步转移之后, 它位于每个状态的概率趋向一个定值。
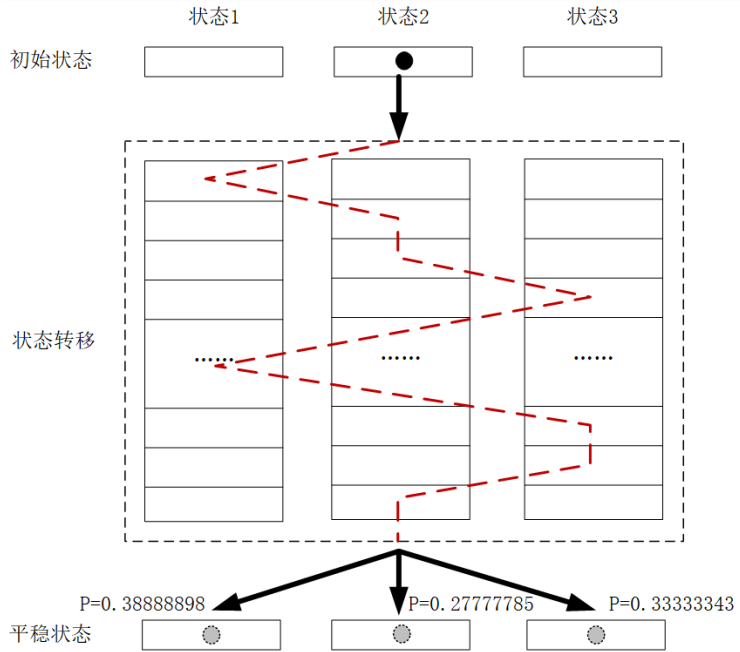
基于马尔科夫链进行采样的思路
背后的大数定律
这里提到的马尔科夫链, 它的状态转移概率矩阵:
\[\begin{matrix} \left[\begin{array}{rr} 0.7 & 0.1 & 0.2 \\ 0.3 & 0.5 & 0.2 \\ 0.1 & 0.3 & 0.6 \end{array}\right] \end{matrix}\]对应的稳态分布是[0.3888, 0.2777, 0.3333]。 如果我们利用大的数据样本, 从任意初始状态出发, 经过足够长的步数转移之后, 我们去统计和计算落入到三个状态中的小石头各自所占的比例, 就可以近似为平稳分布。
利用数值模拟的方法对这个目标平稳分布的采样, 就是基于马尔科夫链的采样方法的思维雏形。
时间分布与空间分布的一致性
如果我们对每一样本都执行依次n步转移, 但是这样计算量相当大, 每次只利用了采样过程中的最后一个状态。
稳态分布的基本定义: 对于一个马尔科夫链, 如果它的状态转移矩阵是P, 稳态分布是$\pi$, 那么它们满足$\pi = P_\pi$的相等关系。
这里的意思就是, 我们只需要对一个小石头进行状态转移就可以实现采样的目标。 即: 在它进入到稳态的那一刻(我们记作时刻$t_0$)开始, 它按照稳态分布中的概率进入到状态1、状态2或者状态3当中的任意一个, 那么当小石头从$t_0$时刻的状态向下一时刻(也就是$t_1$时刻)转移时, 依照$\pi = P_\pi$的相等关系, 这个小石头仍然是依照稳态的概率分布进入到状态1、状态2或者状态3中的任意一个。
这里用时间的平稳分布等价替代了空间的平稳分布
具体实施过程
假设我们需要采样的样本数是N个, 而进入到稳态所需要的转移次数是m次(我们把m次的转移过程称作是燃烧期), 那么我们就记录这一个小球从m到m+N这N次转移的过程中(我们把进入稳态后的转移过程称作是平稳期)的每个时间点所处的状态, 那么我们记录下的这N个状态就一定服从稳态分布中各个状态的概率。
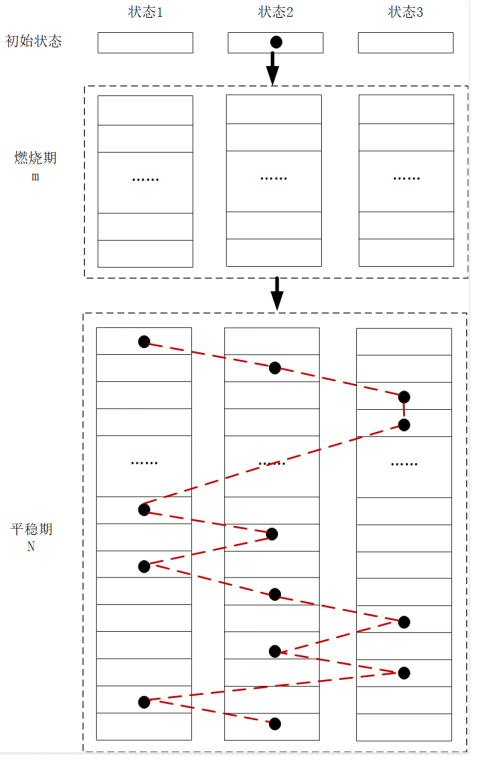
我们只跟踪这一个小石头, 当小石头经过m次转移的燃烧器进入到平稳期之后, 每一次我们都记录下它所处的状态, 我们的采样样本数是N, 那么我们就在平稳期内让小石头按照状态转移矩阵进行N次转移, 从而得到N个采样结果, 这N个采样结果的状态分布就和稳态分布一致。
采样过程的流程总结
- 我们首先曜寻找以目标分布$\pi$为平稳分布的马尔科夫链, 而且这个马尔科夫链的平稳分布是唯一的, 找到它的各个状态的转移概率矩阵P。
- 针对这个马尔科夫链, 我们设定燃烧期m和稳定器N, 随机初始一个状态,在转移概率矩阵的框架下, 在状态间进行m+N次的随机游走, 并记录下每次转移的状态
- 抛弃掉前面m次燃烧期采样得到的状态, 只保留后面平稳期的N次采样结果, 这N次采样结果就近似于目标分布$\pi$的采样。