隐马尔科夫模型
隐马尔可夫模型(Hidden Markov Model, HMM), 在这个模型中, 首先由一个隐藏的马尔科夫链随机生成一个状态随机序列, 再由状态随机序列中的每一个状态对应生成各自的观测, 这些观测组成一个观测随机序列。
因此马尔科夫模型中伴随着两条“线”, 一个是观测随机序列这条“明线”, 另一个是隐藏着的状态随机序列这条“暗线”。
典型实例: 盒子摸球实验
我们有 3 个盒⼦,编号分别为 1 号盒⼦、2 号盒⼦、3 号盒⼦,每个盒⼦⾥都装着个数不等的⿊球和⽩球,具体情况如下⾯ 描述所⽰:
- 1 号盒⼦:⿊球 2 个,⽩球 8 个
- 2 号盒⼦:⿊球 6 个,⽩球 4 个
- 3 号盒⼦:⿊球 4 个,⽩球 6 个
每次先随机出现⼀个盒⼦,然后我们从随机出现的盒⼦中随机摸出⼀个球,并且记录下球的颜⾊,最后把球放回盒 ⼦。下⼀次再随机出现⼀个盒⼦,我们同样地去摸球并记录球的颜⾊。
在试验过程中,我们只能在每次摸出球之后看到被摸出的球的颜⾊,但⽆法知道每次随机出现的盒⼦的编号。
随着试验的进⾏,会依次出现不同编号的盒⼦,这个盒⼦的序列就是我们的状态序列,由于我们始终⽆法观测到盒⼦的编号,因此也就是⼀条隐藏的暗线,也称隐含状态序列。
我们最终能够观察到的是球的颜⾊,因此球的颜⾊序列就是我们的观测序列,也就是我们的明线。
例如,试验重复进⾏ 7 次,其中⼀种可能的观测序列为:$O={⿊, ⿊, ⽩, ⽩, ⽩, ⿊, ⿊}$
我们假定每次盒⼦随机出现的过程是⼀个⻢尔科夫过程,状态集合为:$Q={盒⼦ 1, 盒⼦ 2, 盒⼦ 3},N=3$
每一次各个盒子出现所满足的概率分布如下:
- 1 号盒⼦出现的概率:0.3
- 2 号盒⼦出现的概率:0.5
- 3 号盒⼦出现的概率:0.2
我们用$\pi$表示初始状态的概率向量: $\pi = (0.3, 0.5, 0.2)^T$
各个盒⼦之间相互转换的概率转移图如下图所⽰:
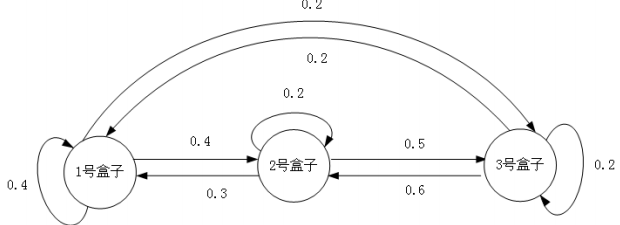
状态转移概率矩阵:
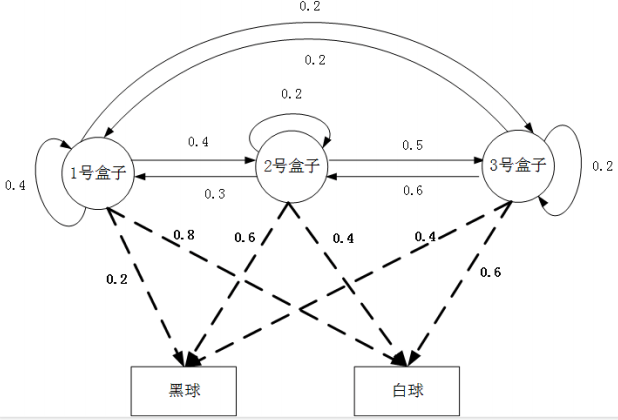
\[A = \begin{matrix} \left[\begin{array}{rr} 0.4 & 0.4 & 0.2 \\ 0.3 & 0.2 & 0.5 \\ 0.2 & 0.6 & 0.2 \end{array}\right] \end{matrix}\]然后是从盒子中摸球的过程,比如在1号盒子中: 黑球2个, 白球8个,采用的是放回式的摸球试验, 这就是最简单的古典概型。从1号盒子中摸出黑球的概率是0.2, 摸出白球的概率是0.8, 也就是所谓的观测概率, 也叫输出概率, 它是从特定的隐含状态中生成指定观测的概率。
同样的, 我们还可以一起把2号盒子和3号盒子的观测概率都集中再一起, 放在同一个矩阵当中, 得到观测概率矩阵:
\[B = \begin{matrix} \left[\begin{array}{rr} 0.2 & 0.8 \\ 0.6 & 0.4 \\ 0.4 & 0.6 \end{array}\right] \end{matrix}\]观测集合: $V = {黑球, 白球}, M=2$
我们重复7次上述过程得到两个序列。
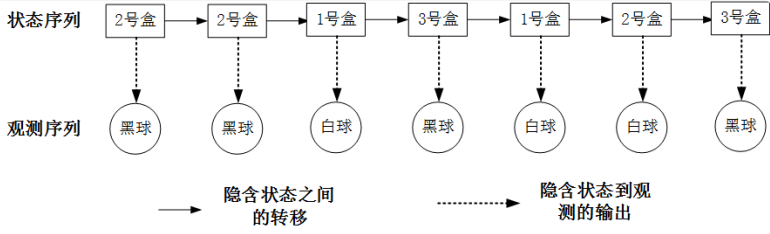
一个是长度为7的隐藏状态序列: $I = {2号盒, 2号盒, 1号盒, 3号盒, 1号盒, 2号盒, 3号盒}$, 这个序列是实际存在的,但是我们无法直接观测到它。
另一个就是对应的长度为7的观测序列: $O = {黑球, 黑球, 白球, 黑球, 白球, 白球, 黑球}$, 这个是我们可以直接通过观测得到的。
在这个盒子摸球实验中, 一明一暗两条线的关系如下图所示:
我们将观测概率也加入状态转移概率图
典型实例:婴⼉的⽇常⽣活
⽐⽅说,⼀个小宝宝有两个典型的状态:饿了和困了,这就是他的状态集,但是小宝宝不会说话表达,因此这个状态就是隐藏的。⽗⺟只能从他所表现出来的⾏为去推测,我们假设他有三种典型的⾏为:${哭闹, 无精打采, 爬来爬去}$
隐含状态之间的转移也是一个马尔科夫过程,从而各个状态所表现出的特定行为也符合一定的概率分布
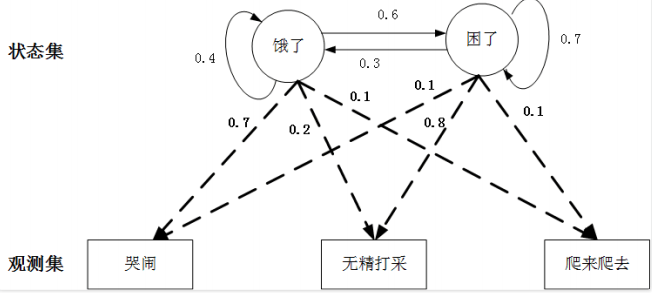
那么这其中的状态集合Q、 观测集合V、状态转移概率矩阵A、观测观测矩阵B, 就很容易通过上面这幅图得到。
隐⻢尔科夫模型的要素提炼
外在表征
隐马尔科夫模型中的关键要素:
- 隐马尔科夫模型中所有的隐含状态构成状态集合: $Q = {q_1, q_2, …, q_N}, 状态个数为N$
- 所有可能的观测构成的集合为: $V = {v_1, v_2, …, v_M}, 观测的个数为M$
- 经过一段时间T后,生成长度为T的状态序列: $I = (i_1, i_2, …, i_T)$
- 对应的观测序列: $O = (o_1, o_2, …, o_T)$
内核三要素
推动隐马尔科夫模型$\lambda$随着时间不断运行的内核时它的三要素: 状态转移矩阵$A$, 观测概率矩阵(也叫输出概率矩阵)$B$, 以及初始隐含状态概率向量$\pi$, 简写成三元组的形式就是: $\lambda = (A, B, \pi)$
其中,初始概率向量$\pi = (\pi_1, \pi_2, \pi_3, …, \pi_N)$, 其中$\pi_i$表示的就是隐含状态序列中第1个状态为$q_i$的概率, 即$\pi_i = P(i_1 = q_i)$
状态转移概率矩阵A本质上就是一个马尔科夫链的转移概率矩阵, 所有可能的隐含状态个数为N, 因此矩阵A是一个$N \times N$的方阵:
\[A = \begin{matrix} \left[\begin{array}{rr} a_{11} & a_{12} & \cdots & a_{1N} \\ a_{21} & a_{22} & \cdots & a_{2N} \\ \cdots & \cdots & \cdots & \cdots \\ a_{N1} & a_{N2} & \cdots & a_{NN} \end{array}\right] \end{matrix}\]观测概率矩阵(输出概率矩阵)B是一个$N \times M$的矩阵, 每一行表示一种状态, 每一行中的概率和为1
\[B = \begin{matrix} \left[\begin{array}{rr} b_{11} & b_{12} & \cdots & b_{1M} \\ b_{21} & b_{22} & \cdots & b_{2M} \\ \cdots & \cdots & \cdots & \cdots \\ b_{N1} & b_{N2} & \cdots & b_{NM} \end{array}\right] \end{matrix}\]模型的关键性质
t时刻隐状态只与前一时刻隐状态相关
隐藏状态的⻢尔科夫链在任意 t 时刻的隐含状态仅仅只依赖于前⼀时刻的隐含状态,而与更早的隐含状态⽆关,当然更与观测⽆关。
这个性质用条件概率的表达式表述如下:
\[P(i_t \mid i_{t-1}, o_{t-1}, i_{t-2}, o_{t-2}, ..., i_1, o_1) = P(i_t \mid i_{t-1}), 其中t = 1, 2, ..., T\]t时刻的观测只与该时刻的隐状态相关
任意时刻的观测只依赖于该时刻隐⻢尔科夫链的隐藏状态,与 其他时刻的隐藏状态和观测⽆关。
同样地, 这个性质也可以用条件概率的表达式进行描述:
\[P(o_t \mid i_t, i_{t-1}, o_{t-1}, ..., i_1, i_1) = P(o_t \mid i_t), 其中t=1, 2, ..., T\]