隐含状态解码问题
解码 Decoding,就是给定⼀个已知的观测序列,求它最有可能对应的状态序列。
⽤形式化的语⾔来说,就是已知模型$\lambda = (A, B, \pi)$和观测序列$O = (o_1, o_2, …, o_T)$, 求使得条件概率$P(I \mid O)$最大的隐状态序列$I = (i_1, i_2, …, i_T)$。
最大路径概率与维特比算法
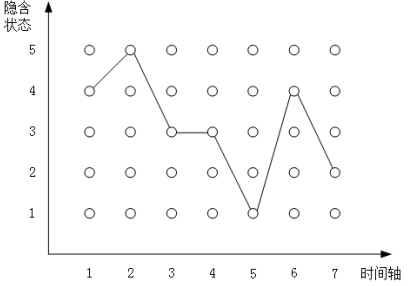
图中展现的隐⻢尔科夫模型中的状态序列,其中⼀共包含 5 种隐含状态,状态序列的⻓度为 7,那么图中很明显横轴是时间 轴,纵轴是状态轴。
我们从整个隐含状态序列的最后往前⾯看,在第 7 个时间点,也就是最后⼀个时间点这,我们要考虑状态序列的最后⼀个状态是状态[1,2,3,4,5] 中的哪⼀个?实质上就是⽐较路径以谁为结束状态,整个路径的概率最⼤。
我们⾸先关注的是最后⼀个时间节点 7,问题就落脚在: 如果状态转移路径以结束于状态 k 的路径概率最⼤, 那么这个概率该怎么表⽰呢?它依赖于时间节点 6 可能选取的 5 个状态。
时间节点 6 取 5 个状态中的任意⼀个都是有可能的,可能由时间节点 6 处的状态 1 转移到时间节点 7 处的状态 k, 也可能由状态 2 转移到时间节点 7 的状态 k,当然也可以是状态 3、状态 4 或者状态 5。最终就看从哪⾥转移过去的路径概率最⼤,就选择从哪⾥转移过去,过程⽰意如下图所⽰:
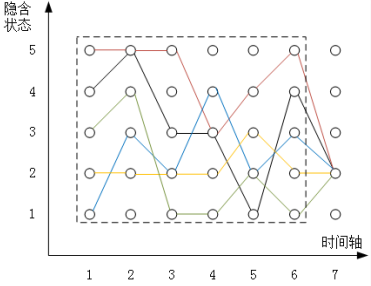
我们令$X_{6i}$表⽰到达时间节点 6 时,此时状态为 i 的最⼤路径概率,当然了,状态 i 可以取 {1,2,3,4,5} 中的任意⼀个,那么实际上就有$X_{61}$、$X_{62}$ 、 $X_{63}$、$X_{64}$、$X_{65}$五个不同的值。在上⾯这幅图中,就对应了虚线框中五种颜⾊⽰意的到达时间节点 6 的五条路径,它们分别都是在时间节点 6 时到达对应状态 i 的最⼤概率路径。
⽤它乘以对应的状态转移概率,即$A_{6i}A_{ik}$,就前进到第 7 个时间节点了。 ⾸先我们固定⼀个第 7 个时间节点结束的状态,⽐如选取状态 1,那么我们可以分别求出从第 6 个时间节点的状态 1、状态 2、状态 3、状态 4、状态 5 分别转移到第 7 个节点状态 1 的概率:$X_{61}A_{11}$、$X_{62}A_{21}$、$X_{63}A_{31}$、$X_{64}A_{41}$、$X_{65}A_{51}$, 我们计算出这 5 个值,取最⼤的就是我们结束于状态 1 的最⼤路径概率。
我们从时间节点 1 出发,正过来,描述⼀下整个过程:
- ⾸先我们在时间节点 1,我们计算出各状态出现的概率,由于只有⼀个节点,因此这个概率值就是此时的最⼤路径概率$X_{1i}$。
- 然后我们再向前前进到时间节点2,对于每⼀个状态j,我们通过利⽤时间节点1的每⼀个状态的最⼤路径概率乘以转移概率,会得到5个到达时间节点2,状态 j 的路径概率值,取最⼤的⼀个就是此时的最⼤路径概率$X_{2j}$。
- 即$X_{2j} = max(X_1A_{ij})$,i 遍历 1、2、3、4、5 每⼀个状态。同时我们还需要记录⼀下此时在时间节点 2、状态 j 这 个节点在获取最⼤路径概率$X_{2j}$的情况下,是由时间节点 1 中的哪个状态转移而来的,把状态序号记录下来。
我们基于时间节点 t,各状态的最⼤路径概率,就可以向前计算出 t+1 各状态的最⼤路径概率,直到最后⼀个时 间节点 T,我们得到时间节点 T 的所有状态的最⼤概率路径$X_{Ti}$ ,取最⼤的⼀个$max(X_{Ti})$,i 遍历 1、2、3、4、5,就是我们要求的最⼤路径概率以及结束的状态,然后依据我们记录的前⼀状态进⾏回溯,就能够把整个状态序列给找出来了。
上述,就是求取最⼤概率路径的过程,也就是⼤名⿍⿍的维特⽐算法。
应用维特比算法进行解码
维特⽐算法中的最⼤概率路径就对应着隐⻢尔科夫模 型中要找的那个最有可能的隐状态序列。
不过此时在计算的过程中,我们不光要考虑隐状态的状态转移概率,还要考虑观测输出概率。
我们要寻找⼀条隐含状态序列$(i_1, i_2, i_3, …, i_t)$,⽤它去⽣成我们指定的观测序列$(o_1, o_2, o_3, …, o_t)$,使得这个观测序列存在的概率最⼤?
⽤公式的语⾔来描述我们的⽬标就是:
\[\delta_t(i) = maxP(i_t=i, i_{t-1}, ..., i_1, o_t, ..., o_1), i=1, 2, 3, ..., N\]它表⽰在时刻 t,结束于隐状态 i,同时满⾜观测序列$(o_1, o_2, …, o_t)$的最⼤路径概率,
依次类推:
\[\delta_{t+1}(i) = max P(i_{t+1}=i, i_t, i_{t-1}, ..., i_1, o_{t+1}, o_t, ..., o_1), i=1, 2, 3, ..., N\]它们的递推关系:
\[\delta_{t+1}(i) = max(\delta_t(j)a_{ji}b_{io_{t+1}}), 1 \leq j \leq N\]和上⾯维特⽐算法中的简单路径概率的例⼦相⽐,其实就是多了⼀个观测输出概率$b_{io_{t+1}}$ ,这个值是已知的,⽐单纯的简单路径概率问题多进⾏⼀次观测输出概率的相乘运算,因此本质上并⽆⼆致。
因此,我们同样地按照维特⽐算法中的思路从$\delta_1(i)$开始起步,⼀步⼀步按照之前介绍过的⽅法推导到$\delta_T(i)$,求得最⼤的概率,同时在递推的过程中,在每⼀个时间点 t 都记录好上⼀个时间点 t-1 的隐含状态,以便于我们最后的状态回溯。
案例实践
⼿动计算
利⽤盒⼦与球的模型来进⾏计算过程的实践。
模型中,隐状态集合 Q={盒⼦ 1, 盒⼦ 2, 盒⼦ 3},N=3,初始概率 。状态概率矩阵为:
\[A = \begin{matrix} \left[\begin{array}{rr} 0.4 & 0.4 & 0.2 \\ 0.3 & 0.2 & 0.5 \\ 0.2 & 0.6 & 0.2 \end{array}\right] \end{matrix}\]观测集合 V={⿊球, ⽩球},M=2。观测概率矩阵:
\[B = \begin{matrix} \left[\begin{array}{rr} 0.2 & 0.8 \\ 0.6 & 0.4 \\ 0.4 & 0.6 \end{array}\right] \end{matrix}\]⾸先初始化,在 t=1 时,隐状态为 i 观测 为⿊球的概率$\delta_1(i)$:
\[\delta_1(1) = \pi_1 b_{1o_1} = 0.3 * 0.2 = 0.06\] \[\delta_1(2) = \pi_2 b_{2o_1} = 0.5 * 0.6 = 0.3\] \[\delta_1(3) = \pi_3 b_{3o_1} = 0.2 * 0.4 = 0.08\]递推到 t=2 时,表⽰在 t=1 时隐状态为 j 号盒⼦,输出观测$o_1 = 黑球$ ,t=2 时隐状态为 i 号盒⼦,输出观测$o_2 = 白球$的最⼤概率:
\[\delta_2(1) = max[\delta_1(j)a_{j1}]b_{1o_2} = max(\delta_1(1)a_{11}, \delta_1(2)a_{21}, \delta_1(3)a_{31})b_{1o_2} \\ = max(0.06*0.4, 0.3*0.3, 0.08*0.2) * 0.8 = max(0.024, 0.09, 0.016) * 0.8 = 0.072\]同时记录 t=1 时的回溯为 j=2 (对应 0.09 的取值)。
\[\delta_2(2) = max[\delta_1(j)a_{j2}]b_{2o_2} = max(\delta_1(1)a_{12}, \delta_1(2)a_{22}, \delta_1(3)a_{32})b_{2o_2} \\ = max(0.06*0.4, 0.3*0.2, 0.08*0.6) * 0.4 = max(0.024, 0.06, 0.048) * 0.4 = 0.024\]同时记录 t=1 时的回溯为 j=2 (对应 0.06 的取值)。
\[\delta_2(3) = max[\delta_1(j)a_{j3}]b_{3o_2} = max(\delta_1(1)a_{13}, \delta_1(2)a_{23}, \delta_1(3)a_{33})b_{3o_2} \\ = max(0.06*0.2, 0.3*0.5, 0.08*0.2) * 0.6 = max(0.012, 0.15, 0.016) * 0.6 = 0.09\]同时记录 t=1 时的回溯为 j=2 (对应 0.15 的取值)。
阶段性的,我们把递推到 t=2 的图像绘制⼀下:
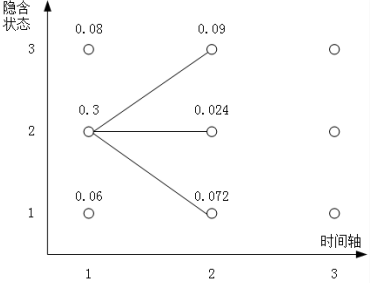
最后我们递推到 t=3:
\[\delta_3(1) = max[\delta_2(j)a_{j1}]b_{1o_3} = max(\delta_2(1)a_{11}, \delta_2(2)a_{21}, \delta_2(3)a_{31})b_{1o_3} \\ = max(0.072*0.4, 0.024*0.3, 0.09*0.2) * 0.2 = max(0.0288, 0.0072, 0.018) * 0.2 = 0.00576\]同时记录 t=2 时的回溯为 j=1 (对应 0.0288 的取值)。
\[\delta_3(2) = max[\delta_2(j)a_{j2}]b_{2o_3} = max(\delta_2(1)a_{12}, \delta_2(2)a_{22}, \delta_2(3)a_{32})b_{2o_3} \\ = max(0.072*0.4, 0.024*0.2, 0.09*0.6) * 0.6 = max(0.0288, 0.0048, 0.054) * 0.6 = 0.0324\]同时记录 t=2 时的回溯为 j=3 (对应 0.054 的取值)。
\[\delta_3(3) = max[\delta_2(j)a_{j3}]b_{3o_3} = max(\delta_2(1)a_{13}, \delta_2(2)a_{23}, \delta_2(3)a_{33})b_{3o_3} \\ = max(0.072*0.2, 0.024*0.5, 0.09*0.2) * 0.4 = max(0.0144, 0.012, 0.018) * 0.4 = 0.0072\]同时记录 t=2 时的回溯为 j=3 (对应 0.018 的取值)。
我们结合观测输出概率,看⼀下此时各个隐状态的路径概率,就得到了如下的这幅图
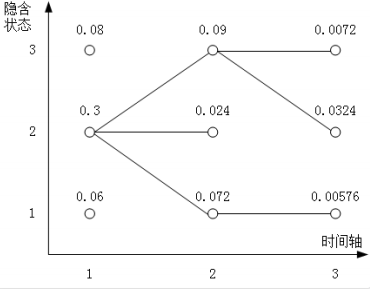
那么我们从最后⼀个时间节点 3 开始,显然选择隐状态 2,它的路径概率最⼤,然后回溯到时间节点 2,按图索骥显然是隐 含状态 3,回溯到时间节点 1,是隐含状态 2。
因此在这个盒⼦与球的模型下,我们最后解码出的隐含状态序列是:
{2 号盒⼦, 3 号盒⼦, 2 号盒⼦}