利⽤矩阵表⽰空间映射
由于矩阵乘法的作⽤,原始向量的空间位置甚⾄其所在空间的维度和形态都发⽣了改变,这便是 矩阵乘法的空间映射作用 。
矮胖矩阵对空间的降维压缩
空间降维的原理
当 m<n 的时候,矩阵是⼀个外表“矮胖“的矩阵,向量 x 是 $R^n$ 空间中的⼀个 n 维向量,x的n个基向量$e_i$分别被矩阵A映射成了n个m维向量, 由于$m < n$, 这一组目标向量所能张成的空间维数最大就是m。
在矩阵A的作用下, 位于$R^n$空间中的任意向量x, 经过映射作用,都转换到了一个维数更低的新空间中的新位置。 “矮胖”矩阵A压缩了原始空间$R^n$。
实际举例
我们用一个$2 \times 3$的矩阵A来举例
\[A = \begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23}\end{bmatrix}\]映射前的向量是$x = \begin{bmatrix}x_1 \ x_2 \ x_3\end{bmatrix}$,它的默认基底是:
\[(\begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}, \begin{bmatrix}0 \\ 1 \\ 0\end{bmatrix}, \begin{bmatrix}0 \\ 0 \\ 1\end{bmatrix})\]经过矩阵 A 的基变换后,这组默认的基底被映射为了三个⽬标向量:
\[(\begin{bmatrix}a_{11} \\ a_{21}\end{bmatrix},\begin{bmatrix}a_{12} \\ a_{22}\end{bmatrix}, \begin{bmatrix}a_{13} \\ a_{23}\end{bmatrix})\]映后的目标向量:
\[x_1\begin{bmatrix}a_{11} \\ a_{21}\end{bmatrix} + x_2\begin{bmatrix}a_{12} \\ a_{22}\end{bmatrix} + x_3\begin{bmatrix}a_{13} \\ a_{23}\end{bmatrix}\]3 个⼆维向量必然是线性相关的,但是仍然分两种情况:
第⼀种情况是:
如果这 3 个⼆维⽬标向量共⾯但不共线,那么其所有的线性组合结果就构成⼆维平⾯$R^2$ ,经过矩阵 A 的映射,整个向量空 间就被压缩成了⼆维,如图
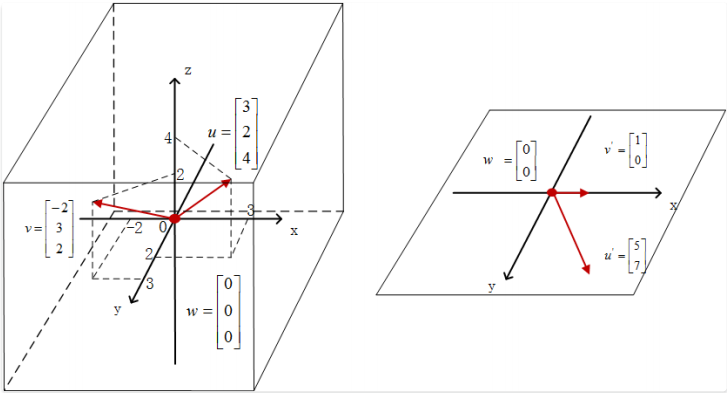
我们按照共⾯不共线的要求设定⼀个映射矩阵:
\[A = \begin{bmatrix}1 & 1 & 0 \\ 1 & 0 & 1\end{bmatrix}\]并在左侧的$R^3$空间中任取三个向量:
\[u = \begin{bmatrix}3 \\ 2 \\ 4\end{bmatrix}, v = \begin{bmatrix}-2 \\ 3 \\ 2\end{bmatrix}, w = \begin{bmatrix}0 \\ 0 \\ 0\end{bmatrix}\]在矩阵A的作用下, 向量u的映射结果是:
\[Au = \begin{bmatrix}1 & 1 & 0 \\ 1 & 0 & 1\end{bmatrix}\begin{bmatrix}3 \\ 2 \\ 4\end{bmatrix} = \begin{bmatrix}5 \\ 7\end{bmatrix}\]向量v的映射结果是:
\[Au = \begin{bmatrix}1 & 1 & 0 \\ 1 & 0 & 1\end{bmatrix}\begin{bmatrix}-2 \\ 3 \\ 2\end{bmatrix} = \begin{bmatrix}1 \\ 0\end{bmatrix}\]向量w的映射结果是二维$\begin{bmatrix}0 \ 0\end{bmatrix}$
第⼆种情况:
如果这3个二维向量共线, 那么其线性组合就只能分布在二维平面$R^2$中的一条过原点(0, 0)的直线上, 经过矩阵的映射, 整个向量空间被压缩成了一维, 如图所示:
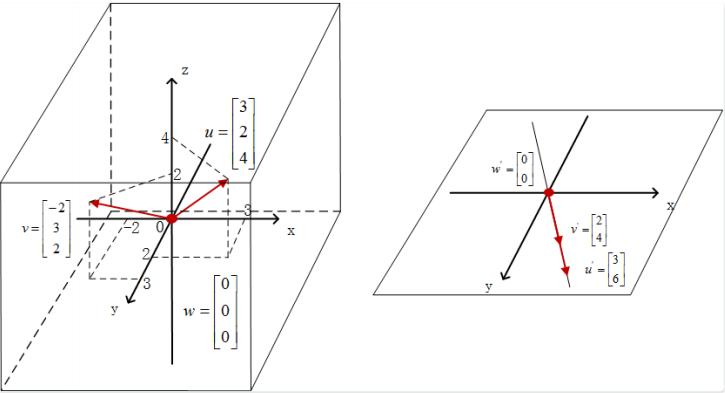
同样,为了直观演⽰这个降维压缩的过程,我们选取⼀个列向量共线的矩阵 A:
\[A = \begin{bmatrix}1 & 2 & -1 \\ 2 & 4 & -2\end{bmatrix}\]依然取上个例子中的三个三维向量:
\[u = \begin{bmatrix}3 \\ 2 \\ 4\end{bmatrix}, v = \begin{bmatrix}-2 \\ 3 \\ 2\end{bmatrix}, w = \begin{bmatrix}0 \\ 0 \\ 0\end{bmatrix}\]向量u的映射结果是:
\[Au = \begin{bmatrix}1 & 2 & -1 \\ 2 & 4 & -2\end{bmatrix}\begin{bmatrix}3 \\ 2 \\ 4\end{bmatrix} = \begin{bmatrix}3 \\ 6\end{bmatrix}\]向量v的映射结果是:
\[Av = \begin{bmatrix}1 & 2 & -1 \\ 2 & 4 & -2\end{bmatrix}\begin{bmatrix}-2 \\ 3 \\ 2\end{bmatrix} = \begin{bmatrix}2 \\ 4\end{bmatrix}\]向量 w 的映射结果仍然是⼆维的零向量$\begin{bmatrix}0 \ 0\end{bmatrix}$
⾼瘦矩阵⽆法覆盖⽬标空间
原理:向量信息不增加
即 m×n 矩阵中的 m>n 这种情况,我们称之为“⾼瘦”矩阵。
x 的 n 个基向量 分别被矩阵 A 映射成了 n 个 m 维向量,由于 m>n,看上去 x 映射后的⽬标向量的维数提⾼了,变成了 m维。
那我们能不能说:经过矩阵 A 的映射,原始向量 x 构成的空间$R^n$变成了维数更⾼的空间$R^m$呢?答案是否定的,哲学点说,⼀个事物⽆中⽣有,那是不可能的,平⽩⽆故地⼀个向量携带的信息怎么能增加呢?
实际举例
我们用一个实际的$3 \times 2$矩阵来举例:
\[A = \begin{bmatrix}a_{11} & a_{12} \\ a_{21} & a_{22} \\ a_{31} & a_{32}\end{bmatrix}\]映射前的原始向量是二维空间中的$x = \begin{bmatrix}x_1 \ x_2\end{bmatrix}$。映射的过程是:
\[Ax = \begin{bmatrix}a_{11} & a_{12} \\ a_{21} & a_{22} \\ a_{31} & a_{32}\end{bmatrix} \begin{bmatrix}x_1 \\ x_2\end{bmatrix} = x_1 \begin{bmatrix}a_{11} \\ a_{21} \\ a_{31}\end{bmatrix} + x_2 \begin{bmatrix}a_{12} \\ a_{22} \\ a_{32}\end{bmatrix}\]由于映射前的向量x是二维空间$R^2$中的任意向量, $x_1$和$x_2$取任意数, 因此在矩阵A的作用下, 整个二维空间的映射结果就是$\begin{bmatrix}a_{11} \ a_{21} \ a_{31}\end{bmatrix}$和$\begin{bmatrix}a_{12} \ a_{22} \ a_{32}\end{bmatrix}$这两个向量的张成空间。
我们对这两个三维向量, 同样分两种情况:
第一种情况是
两个向量线性无关, 那么张成空间就是一个二维平面, 这个二维平面不是一个前面见过的由x轴和y轴构成的$R^2$的平面。
我们仍然举⼀个实际的例⼦:
\[A = \begin{bmatrix}1 & 0 \\ 0 & 1 \\ 0 & -1\end{bmatrix}\]我们还是在原空间$R^2$内选取三个向量进行映射:
\[u = \begin{bmatrix}1 \\ 1\end{bmatrix}, v = \begin{bmatrix}-1 \\ 1\end{bmatrix}, w = \begin{bmatrix}0 \\ 0\end{bmatrix}\]映射后地结果分别是:
\[Au = \begin{bmatrix}1 & 0 \\ 0 & 1 \\ 0 & -1\end{bmatrix}\begin{bmatrix}1 \\ 1\end{bmatrix} = \begin{bmatrix}1 \\ 1 \\ -1\end{bmatrix}\] \[Av = \begin{bmatrix}1 & 0 \\ 0 & 1 \\ 0 & -1\end{bmatrix}\begin{bmatrix}-1 \\ 1\end{bmatrix} = \begin{bmatrix}-1 \\ 1 \\ -1\end{bmatrix}\]而向量w经过矩阵映射后,仍是三维空间中的0向量, 如图所示:
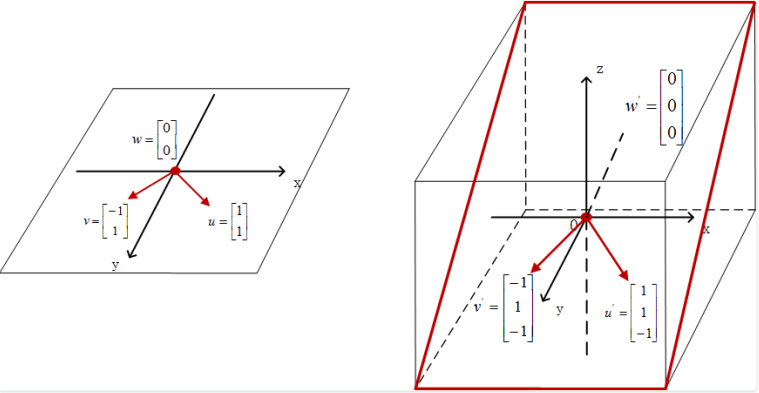
我们再讨论第二种情况
如果两个向量线性相关, 那么张成空间就是一条直线, 那么同样, 这个直线式经过零点, 并“斜穿”过三维空间$R^3$的一条直线。
我们举一个实例:
\[A = \begin{bmatrix}1 & 2 \\ 1 & 2 \\ -1 & -2\end{bmatrix}\]我们仍然选取上文中的三个向量进行映射:
\[u = \begin{bmatrix}1 \\ 1\end{bmatrix}, v = \begin{bmatrix}-1 \\ 1\end{bmatrix}, w = \begin{bmatrix}0 \\ 0\end{bmatrix}\]映射后的结果分别是:
\[Au = \begin{bmatrix}1 & 2 \\ 1 & 2 \\ -1 & -2\end{bmatrix}\begin{bmatrix}1 \\ 1\end{bmatrix} = \begin{bmatrix}3 \\ 3 \\ -3\end{bmatrix} Au = \begin{bmatrix}1 & 2 \\ 1 & 2 \\ -1 & -2\end{bmatrix}\begin{bmatrix}-1 \\ 1\end{bmatrix} = \begin{bmatrix}1 \\ 1 \\ -1\end{bmatrix}\]而向量w经过矩阵映射后, 仍是三维空间中的零向量, 如图所示:
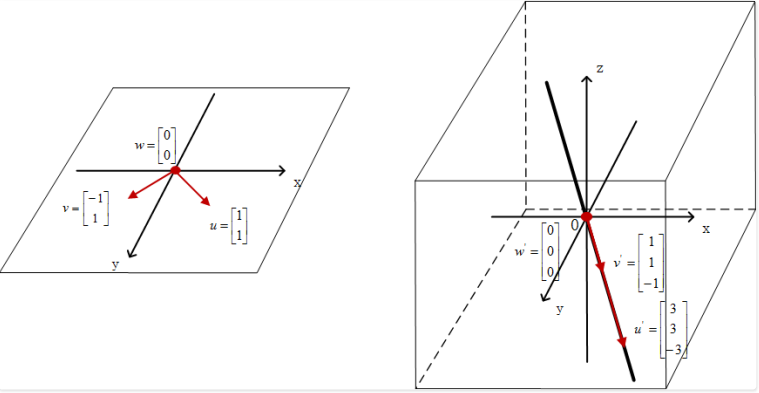
分多种情况的⽅阵映射
⾄于说如果矩阵 A 是⼀个 n 阶⽅阵,分析⽅法也是⼀样的,核⼼问题仍然是分析 A 的各列向量的线性相关性,我们很容易发现, $R^n$空间中的向量经过矩阵 A 的映射,其⽬标空间的维度就是这 n 个 n 维列向量的张成空间的维度,其映射空间的维度必然小于等于 n。
- 情况⼀: 当这三个列向量共⾯但不共线的时候, $R^3$空间中的向量经过映射,最后分布在“搭”在三维空间$R^3$中的 ⼀个平⾯上。
- 情况⼆: 当这三个列向量共线的时候, $R^3$空间中的向量经过映射,最后分布在“穿”过三维空间$R^3$中的⼀条直线 上。
空间映射形态的决定因素
矩阵的秩
我们把⼀个空间经过矩阵映射后得到的新空 间称之为它的像空间。
⼀个原始空间,经过⼏个形状相同的矩阵进⾏映射,像空间的维数可能不同;经过⼏个不同形状的矩阵进⾏映 射,⼜有可能得到维数相同的像空间。那么决定因素是什么?
决定因素就是空间映射矩阵的列向量,列向量张成空间的维数就是原始空间映射后的像空间维数。我们给矩阵列向量的张成 空间维数取了⼀个名字,就叫作: 矩阵的秩