两个问题
如果线性⽅程组⽆解怎么办
我们看看下⾯这个⽅程组:
\[2x + y = 4 \\ x + 2y = 3 \\ x + 4y = 9\]很明显,这个⽅程组没有解。但是我们不能仅仅停留在这⾥,因为实际⼯程领域如果出现这种情况,该如何去解决?换句话 说,我们如何尽可能地找到⼀$\begin{bmatrix}x \ y\end{bmatrix}$, 使得利⽤它让⽅程组左侧得到的结果离右侧$\begin{bmatrix}4 \ 3 \ 9\end{bmatrix}$的距离最近?
如果直线⽆法穿过所有点怎么处理
我们知道在平⾯上任取两个点,⼀定能找到⼀条通过它们的直线。但是如果有三个点、四个点甚⾄更多呢?⽐如下⾯这种情 况:
我们在平⾯上取三个点:(0,1)、(1,4)、(2,3),能找到⼀条直线同时通过这三个点么?答案是不⾏。那么该如何解决?我们 退⼀步,能否找到⼀条直线,距离这三个点的距离最近?
从投影的⻆度来定义“最近”
在空间中有⼀个穿过原点的直线,并且沿着向量 a 的⽅向,在空间中有⼀个点 b,它不在直线上,如何在这条直线找到⼀个 点,使之距离点 b 最近?
这个问题⼤家会觉得很简单,当然是通过 b 点,向直线做⼀条垂线就能获得最短距离,其中我们要寻找的点就是垂线与直线 的交点。如图所⽰:
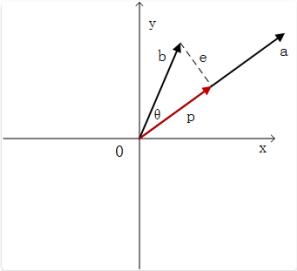
向量 b 和向量 a 的夹⻆是 ,因此通过 b 点到直线的最近距离是$\mid b \mid sin \theta$ 。向量 p,从原点出发到垂直交点的向量,它是向量 b 在向量 a 上的投影。而向量 e=b-p 我们称之为误差向量,它的⻓度就是我们 要寻找的最近距离。
利⽤矩阵⼯具来描述投影
向⼀维直线投影
我们将向量 a 作为这个直线的基向量,向量 p 就 可以⽤ a 来表⽰,记作: $p = \hat x a$( $\hat x$是⼀个标量),我们的⽬标就是求取$\hat x$ ,投影向量 p 和投影矩阵 P。
我们仍然把握⼀个核⼼,就是误差向量 e 和基向量 a 的垂直关系,因此有 $a · e = 0$,我们进⼀步展开:
\[a · e = 0 \Rightarrow a · (b - p) = 0 \Rightarrow a · (b - \hat x a) = 0\] \[a · b - \hat x a · a = 0 \Rightarrow \hat x = \frac{a · b}{a · a}\]$a · b = a^T b$, 因此最终有
\[x = \frac{a^T b}{a^T a}\]投影向量:
\[p = a \hat x = a \frac{a^T b}{a^T a}a\]最后我们探索将向量b变换到其投影p的投影变换矩阵。
由于$p = \hat x a$是标量与向量的乘法,因此交换一下位置: $p = a \hat x$同样成立, 于是有:
\[p = a \hat x = a \frac{a^T b}{a^T a} = \frac{aa^T}{a^Ta}b\]由此得到投影矩阵:
\[P = \frac{a a^T}{a^T a}\]⼀维直线投影举例
我们举一个简单的例子, 向量$a = \begin{bmatrix}1 \ 2 \ 3\end{bmatrix}$, 我们来寻找向量$b = \begin{bmatrix}1 \ 1 \ 1\end{bmatrix}$在该向量上的投影向量p以及任意向量a上的投影矩阵P。
我们先求一下投影向量p:
\[\hat x = \frac{a^T b}{a^T a} = \frac{\begin{bmatrix}1 & 2 & 3\end{bmatrix}\begin{bmatrix}1 \\ 1 \\ 1\end{bmatrix}}{\begin{bmatrix}1 & 2 & 3\end{bmatrix}\begin{bmatrix}1 \\ 2 \\ 3\end{bmatrix}} = \frac{3}{7}\]因此有:
\[p = \hat x a = \frac{3}{7} \begin{bmatrix}1 \\ 2 \\ 3\end{bmatrix}\]接下来我们求向a投影的矩阵P:
\[P = \frac{aa^T}{a^T a} = \frac{\begin{bmatrix}1 \\ 2 \\ 3\end{bmatrix}\begin{bmatrix}1 & 2 & 3\end{bmatrix}}{\begin{bmatrix}1 & 2 & 3\end{bmatrix}\begin{bmatrix}1 \\ 2 \\ 3\end{bmatrix}} = \frac{1}{14}\begin{bmatrix}1 & 2 & 3 \\ 2 & 4 & 6 \\ 3 & 6 & 9\end{bmatrix}\]最后对前后两次运算的结果进行一下校验:
\[p = Pb = \frac{1}{14} \begin{bmatrix}1 & 2 & 3 \\ 2 & 4 & 6 \\ 3 & 6 & 9\end{bmatrix}\begin{bmatrix}1 \\ 1 \\ 1\end{bmatrix} = \frac{1}{14}\begin{bmatrix}6 \\ 12 \\ 18\end{bmatrix} = \frac{3}{7}\begin{bmatrix}1 \\ 2 \\ 3\end{bmatrix}\]结果一致。
向⼆维平⾯投影
我们将问题拓展到⼆维平⾯,这个⼆维平⾯不仅仅局限于$R^2$平⾯,而是空间中任意过原点的⼆维平⾯,我们假设 这个⼆维平⾯是$R^m$的⼦空间,如果空间中同样有⼀个向量 b,我们想在这个⼆维平⾯上寻找⼀个与之距离最近的向量,那么同理也是去寻找向 量 b 在平⾯上的投影向量 p。如图所示:
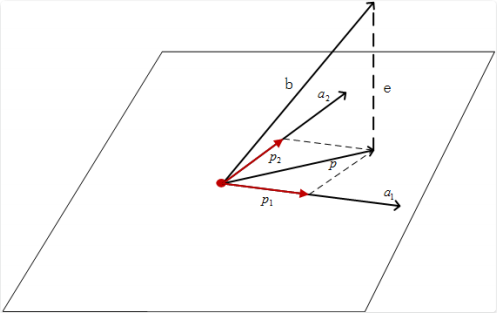
同样,我们去做向量 b 到⼆维平⾯的垂线。⼏何的常识告诉我们,⼀条直线如果与⼀条平⾯垂直,则它与该平⾯上的所有向量垂直。
选取⼆维平⾯上线性⽆关的两个向量 $a_1$、 $a_2$作为这个平⾯的⼀组基(因为我们假设这个⼆维平⾯是$R^m$的⼦空间,因此, $a_1$和$a_2$是 m 维的列向量), 由于平⾯上所有的向量都可以写成这组基$a_1$和$a_2$的线性组合的形式,那么只要保证误差向量 e 与$a_1$ 、$a_2$分别垂直,就能保证向量 e 与整个平⾯垂直,向量 p 就是向量 b 在平⾯上的投影向量。
从直线上的⼀个向量垂直的表达式拓展到平⾯上的两个垂直的表达式,我们从下⾯两个式⼦⼊⼿: $a_1 · e = 0$和$a_2 · e = 0$ ,其中,$e = b - p$。
这⾥的投影向量 p 该如何表⽰呢?投影向量 p 也在这个平⾯上,⾃然也是基向量 和 的线性组合,我们记作:$p = p_1 + p_2 = \hat x_1 a_1 + \hat x_2 a_2$。
如果⽤矩阵来进⼀步概括的话,我们可以把$a_1$和$a_2$作为矩阵 A 的列向量, 记作$A = \begin{bmatrix}a_1 & a_2\end{bmatrix}, \hat x = \begin{bmatrix}\hat x_1 \ \hat x_2\end{bmatrix}$, 因此投影向量可以被概括为: $p = A \hat x$。
代入上面两个向量垂直的等式:
\[a_1 · e = 0 \Rightarrow a_1 · (b - p) \Rightarrow a_1^T(b - A\hat x) = 0\]同理也有:
\[a_2^T(b - A \hat x) = 0\]把这两个等式结合放在一个矩阵乘法里:
\[\begin{bmatrix}a_1^T \\ a_2^T\end{bmatrix}(b - A \hat x) = 0\]我们之前让$A = \begin{bmatrix}a_1 & a_2\end{bmatrix}$, 那么就有$A^T = \begin{bmatrix}a_1^T \ a_2^T\end{bmatrix}$。
我们就得到这个等式:
\[A^T(b - A \hat x) = 0 \Rightarrow A^T A \hat x = A^T b\]假设这个⼆维平⾯是$R^m$空间中的⼀个⼦空间,那么$a_1$和$a_2$都是 m 维列向量(显然$m \geq 2$ ),因此矩阵 A 就是⼀个 m×2 且两列线性⽆关的矩阵。 因此$A^T A$的结果是一个二阶可逆矩阵。
为什么可逆?
由于矩阵 A 的各列线性⽆关,因此 A 是列满秩矩阵,其零空间 N(A) 就是⼀个 0向量,如果我们能证明$A^TA$的零空间和矩阵 A 的零空间⼀致,那么就能知道$A^TA$也是满秩⽅阵,即可逆。
我们先看$A \Rightarrow A^TA$这个⽅向,如果 Ax=0,那么$A^T(Ax)=0$ 必然成⽴,于是就有$(A^TA)x = 0$ 。 再看$A^TA \Rightarrow A$这个⽅向,如果$(A^TA)x = 0$ ,那么$x^TA^TAx = 0$,稍微处理⼀下:$(Ax)^TAx=0$ ,即得出了 Ax=0。
因此最终有:$\hat x = (A^T A)^{-1} A^T b$。
单独的矩阵$A$和$A^T$首先连方阵都不能保证,因此不能对它们单独讨论可逆性。 一定将可逆操作加载$(A^T A)$这个整体上。
因此投影向量p的表示方法是:
\[p = A \hat x = A(A^T A)^{-1} A^T b\]从投影矩阵P的角度来看, 有$p = Pb$, 因此$P = A(A^T A)^{-1}A^T$, 从维度来判断, 它是一个m阶的方阵。
二维平面投影举例
我们也举一个简单的例子:
空间中有一个向量$b = \begin{bmatrix}3 \ 0 \ 0\end{bmatrix}$, 投影平面的基是$\begin{bmatrix}1 \ 2 \ 3\end{bmatrix}$和$\begin{bmatrix}0 \ 1 \ 1\end{bmatrix}$。 我们求一下投影向量$p$和投影矩阵$P$。
我们将两个基向量作为矩阵A的列向量:
\[A = \begin{bmatrix}1 & 0 \\ 2 & 1 \\ 3 & 1\end{bmatrix}\]其中:
\[A^T A = \begin{bmatrix}1 & 2 & 3 \\ 0 & 1 & 1\end{bmatrix}\begin{bmatrix}1 & 0 \\ 2 & 1 \\ 3 & 1\end{bmatrix} = \begin{bmatrix}14 & 5 \\ 5 & 2\end{bmatrix}\] \[(A^T A)^{-1} = \begin{bmatrix}14 & 5 \\ 5 & 2\end{bmatrix}^{-1} = \frac{1}{3}\begin{bmatrix}2 & -5 \\ -5 & 14\end{bmatrix}\] \[P = A \hat x = A(A^TA)^{-1}A^T = \frac{1}{3}\begin{bmatrix}1 & 0 \\ 2 & 1 \\ 3 & 1\end{bmatrix}\begin{bmatrix}2 & -5 \\ -5 & 14\end{bmatrix}\begin{bmatrix}1 & 2 & 3 \\ 0 & 1 & 1\end{bmatrix} = \frac{1}{3}\begin{bmatrix}2 & -1 & 1 \\ -1 & 2 & 1 \\ 1 & 1 & 2\end{bmatrix}\]得到了投影矩阵, 得投影向量:
\[p = Pb = \frac{1}{3}\begin{bmatrix}2 & -1 & 1 \\ -1 & 2 & 1 \\ 1 & 1 & 2\end{bmatrix}\begin{bmatrix}3 \\ 0 \\ 0 \end{bmatrix} = \begin{bmatrix}2 \\ -1 \\ 1\end{bmatrix}\]向n维子空间投影的一般情况
有了向 2 维平⾯投影的推导过程,其实向$^m$空间中的 n 维⼦空间投影这个⼀般化的问题,就⾮常简单了。其核⼼仍然是原 始向量 b 与投影向量 p 的向量之差:即误差向量 e=b-p 与这个 n 维⼦空间垂直。
然后问题转化为在这个 n 维⼦空间中寻找 n 个线性⽆关的向量$a_1, a_2, …, a_n$作为这个⼦空间的⼀组基,然后使得向量 e与这⼀组基向量分别垂直。
⾸先满⾜:
\[a_1 · e = 0, a_2 · e = 0, ..., a_n · e = 0\]然后投影向量依旧表示为这组基的线性组合:
\[p = \hat x a_1 + \hat x_2 a_2 + ... + \hat x_n a_n\]我们依旧分别用矩阵来表示:
\[A = \begin{bmatrix} a_1, a_2, ..., a_n\end{bmatrix}, \hat x = \begin{bmatrix}\hat x_1 \\ \hat x_2 \\ \cdots \\ \hat x_n\end{bmatrix}\]投影向量依旧写成$p = A \hat x$, 依然是$e = b - A \hat x$。
最终我们把n个$a_k · e = 0 \Rightarrow a_k^T(b - A \hat x)$统一起来:
\[\begin{bmatrix}a_1^T \\ a_2^T \\ \cdots \\ a_n^T\end{bmatrix}(b - A\hat x) = 0\]之后的过程也都是⼀模⼀样:
\[A^T(b - A \hat x) = 0 \Rightarrow A^TA \hat x = A^T b\]此时A是一个$m \times n$的矩阵, 由于这是一个$R^m$中的n维子空间,因此必有$m \geq n$, 所以同样有结论, $A^TA$是n阶可逆方阵。
最终的计算结果和二维平面的投影是一模一样的:
\[\hat x = (A^TA)^{-1}A^T b\] \[p = A \hat x = A(A^T A)^{-1} A^T b\] \[P = A(A^T A)^{-1} A^T\]