基底不同,向量的坐标值就不同
向量在空间中的位置是绝对的,而其坐标值却是相对的,坐标的取 值依托于其所选取的基底。
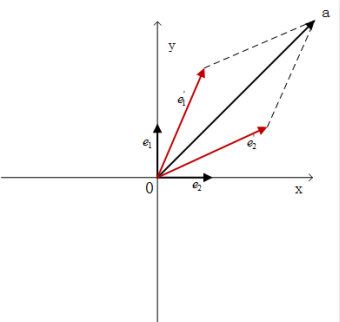
我们看到,图中的向量 a,它在空间中的位置是固定的,如果我们使⽤第⼀组基底 $e_1, e_2$,即$(\begin{bmatrix}1 \ 0\end{bmatrix}, \begin{bmatrix}0 \ 1\end{bmatrix})$ ,向量 a 表⽰ 为$3\begin{bmatrix}1 \ 0\end{bmatrix} + 3\begin{bmatrix}0 \ 1\end{bmatrix}$ ,那么在此基底下,向量 a 的坐标为$\begin{bmatrix}3 \ 3\end{bmatrix}$。
我们使用红色的两个向量$(e_1’, e_2’)$作为基底, 这两个基向量在$(e_1, e_2)$为基底的请款下其坐标分别为$\begin{bmatrix}2 \ 1\end{bmatrix}$和$\begin{bmatrix}1 \ 2\end{bmatrix}$,那么向量a在以$(e_1’, e_2’)$为基底的情况下, 则表示为$1\begin{bmatrix}2 \ 1\end{bmatrix} + 1\begin{bmatrix}1 \ 2\end{bmatrix}$, 其坐标即为$\begin{bmatrix}1 \ 1\end{bmatrix}$。
描述线性变换的矩阵也取决于基底
基底不同,描述向量线性变换的矩阵也不同
静态的向量,我们选取的基底不同,⽤于表⽰静态向量的坐标值就不同。
对于动态的向量变换, 向量从某个空间中的 位置 P 移动到位置 Q,我们知道可以⽤矩阵来表⽰向量空间位置的改变,如果我们选取的基底不同,同⼀个运动在不同基底下,显然对应的矩 阵表⽰也是不同的。
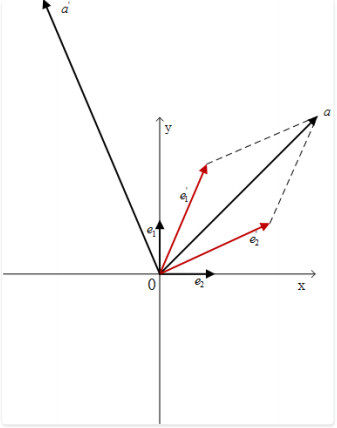
在这个二维空间$R^2$中, 向量从$a$变换到$a’$。 在基底$(\begin{bmatrix}1 \ 0\end{bmatrix}, \begin{bmatrix}0 \ 1\end{bmatrix})$的描述下, 其坐标从$\begin{bmatrix}3 \ 3\end{bmatrix}$变换到$\begin{bmatrix}-3 \ 6\end{bmatrix}$, 对应于这个线性变换的矩阵为$\begin{bmatrix}1 & -2 \ 1 & 1\end{bmatrix}$。 但是如果在基底$(\begin{bmatrix}2 \ 1\end{bmatrix}, \begin{bmatrix}1 \ 2\end{bmatrix})$的描述下, 其坐标的转换变成了$\begin{bmatrix}1 \ 1\end{bmatrix} \Rightarrow \begin{bmatrix}-4 \ 5\end{bmatrix}$, 显然前一个基底下的变换矩阵$\begin{bmatrix}1 & -2 \ 1 & 1\end{bmatrix}$就无法表示这个基底下的变换了, 因为$\begin{bmatrix}1 & -2 \ 1 & 1\end{bmatrix}\begin{bmatrix}1 \ 1\end{bmatrix} \neq \begin{bmatrix}-4 \ 5\end{bmatrix}$。
相似矩阵与相似变换
针对指定向量的同⼀个空间变换,⽤来在不同基底下进⾏描述的不同矩阵,彼此之间称之为相似矩阵。相似矩阵所表⽰的线 性变换,彼此之间称之为相似变换。
利⽤基底变换推导相似矩阵间的关系式
在基底$(e_1, e_2)$下, 坐标为x的向量通过矩阵A完成了线性变换, 线性变换后的坐标为$x’$。
我们也可以通过矩阵P, 将向量变换到$(e_1’, e_2’)$下的坐标表示, 记作$P_x$。这时在新的基底下,用来表示我们上面同一个空间变换的是另一个矩阵B, 即基底$(e_1’, e_2’)$下变换后的目标坐标为$BP_x$。
我们再次把坐标从基底$(e_1’, e_2’)$变回到$(e_1, e_2)$下, 即左乘一个逆矩阵$P^{-1}$,因此和最初直接用矩阵A变换殊途同归。
即矩阵变换$A = P^{-1}BP$, 其中矩阵A和B就是相似矩阵, 表示了向量在两个基底$(e_1, e_2)$和$(e_1’, e_2’)$下的相似变换。
相似矩阵的转换关系与各⾃基底的转换关系相对应
那具体这个矩阵 P 该如何表⽰呢,或是说它是如何得到的?我们来分析⼀下这个过程,即:向量在空间中发⽣⼀次线性变 换,由空间位置 M 变到空间位置 N。如图所⽰:
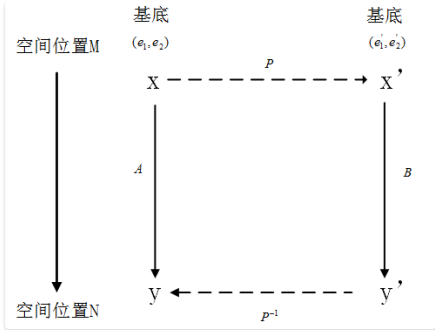
我们假设讨论的前提是: 在基底$(e_1, e_2)$下, 向量在矩阵A的作用下由坐标x变成坐标y, 在基底$(e_1’, e_2’)$下, 向量在矩阵B的作用下由坐标$x’$变成坐标$y’$, 同时$x’ = Px$。
在基底$(e_1, e_2)$下, 向量表示为$ae_i + be_j$, 其坐标为$x = \begin{bmatrix}a \ b\end{bmatrix}$, 如果在基底$(e_1’, e_2’)$下坐标该如何表示?我们假设两组基底的线性关系如下: $e_i = ce_i’ + de_j’, e_j = fe_i’ + ge_j’$, 明确了这层关系, 我们就很容易的做一个基底变换:
在基底$(e_1’, e_2’)$下, 向量表示为:
\[ae_i + be_j = a(ce_i' + de_j') + b(fe_i' + ge_j') = (ac + bf)e_i' + (ad + bg)e_j'\]其坐标为:
\[x' = \begin{bmatrix}ac + bf \\ ad + bg\end{bmatrix}\]坐标可以分解成:
\[x' = \begin{bmatrix}c & f \\ d & g\end{bmatrix}\begin{bmatrix}a \\ b\end{bmatrix}\]即
\[x' = \begin{bmatrix}c & f \\ d & g\end{bmatrix}x\]那么P就得出来了, $P=\begin{bmatrix}c & f \ d & g\end{bmatrix}$, 与两组基底之间的线性关系是完全对应的。
相似矩阵的⽤途:矩阵的对⻆化
对⻆矩阵的两⼤优势
对⻆矩阵有以下两⼤优势:
⼀⽅⾯是:⼀个 n 维列向量在 n 阶对⻆矩阵的作⽤下,其线性变换的⽅式仅仅反映在各个维度轴向上的拉伸,而不对应平 移或者旋转,即:
\[Ax = \begin{bmatrix}a_1 & & \\ & a_2 & \\ & & a_3\end{bmatrix}\begin{bmatrix}x_1 \\ x_2 \\ x_3\end{bmatrix} = \begin{bmatrix}a_1x_1 \\ a_2x_2 \\ a_3x_3\end{bmatrix}\]另⼀⽅⾯是,体现在连续的线性变换上,我们可以看出:
\[A · A = \begin{bmatrix}a_1 & & \\ & a_2 & \\ & & a_3\end{bmatrix} \begin{bmatrix}a_1 & & \\ & a_2 & \\ & & a_3\end{bmatrix} = \begin{bmatrix}a_1^2 & & \\ & a_2^2 & \\ & & a_3^2\end{bmatrix}\]因此推而⼴之有:
\[A^n = \begin{bmatrix}a_1 & & \\ & a_2 & \\ & & a_3\end{bmatrix}^n = \begin{bmatrix}a_1^n & & \\ & a_2^n & \\ & & a_3^n\end{bmatrix}\]对⻆矩阵反映的是⼀种⾮常简便的线性变换。