特征值分解的⼏何意义
通过特征值分解(EVD)的⽅法对样本的特征提取主成分,从而实现数据的降维。在介绍奇异值分解 (SVD)之前,我们再着重挖掘⼀下特征值分解的⼏何意义。
分解过程回顾
我们最开始获得的是⼀组原始的$m \times n$数据样本矩阵 A,其中,m 表⽰特征的个数,n 表⽰样本的个数。通过与⾃⾝转置 相乘: $AA^T$得到了样本特征的 m 阶协⽅差矩阵 C,通过求取协⽅差矩阵 C 的⼀组标准正交特征向量$q_1, q_2, …, q_m$ 以及对应的特征值$\lambda_1, \lambda_2, …, \lambda_m$ 。
我们这⾥处理的就是协⽅差矩阵 C,对 C 进⾏特征值分解,将矩阵分解成了
\[C = \begin{bmatrix}q_1 & q_2 & ... & q_m\end{bmatrix} \begin{bmatrix}\lambda_1 & & & \\ & \lambda_2 & & \\ & & ... & \\ & & & \lambda_m\end{bmatrix} \begin{bmatrix}q_1^T \\ q_2^T \\ ... \\ q_m^T\end{bmatrix}\]最终,我们选取前 k 个特征向量构成数据压缩矩阵 P 的各⾏,通过 PA 达到数据压缩的⽬的。
⼏何意义剖析
为了完成矩阵的特征值分解,最最关键还是要回归到这个基本性质上来:$Cq_i = \lambda_i q_i$。
结合主成分分析的推导过程我们知道,协⽅差矩阵 C 之所以能够分解,是因为在原始空间$R^m$中, 我们原本默认是⽤$e_1, e_2, …, e_m$这组默认基向量来表⽰我们空间中的任意⼀个向量 a,如果我们采⽤基变换,将 a ⽤ $q_1, q_2, …, q_m$这组标准正交基来表⽰后,Ca 的乘法运算就变得很简单了,只需要在各个基向量的⽅向上对应伸⻓$\lambda_i$倍即可,如图所 ⽰:
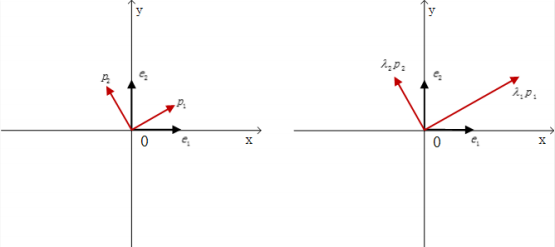
实际上,我们之前也重点分析过,因为协⽅差矩阵具备对称性、正定性,保证了它可以被对⻆化,并且特征值⼀定为正,从 而使得特征值分解的过程⼀定能够顺利完成。 因此利⽤特征值分解进⾏主成分分析,核⼼就是获取协⽅差矩阵,然后对其进⾏矩阵分解,获得⼀组特征值和其对应的⽅向。
从$Av = \sigma u$⼊⼿奇异值分解
但是,如果我们不进⾏协⽅差矩阵 C 的求取,绕开它直接对原始的数据采样矩阵 A 进⾏矩阵分解,从而进⾏降维操作,⾏ 不⾏?
如果继续沿⽤上⾯的办法,显然是不⾏的,特征值分解对矩阵的要求很严,⾸先得是⼀个⽅阵,其次在⽅阵的基础上,还得 满⾜可对⻆化的要求。但是原始的$m \times n$数据采样矩阵 A 连⽅阵这个最基本的条件都不满⾜,是根本⽆法进⾏特征值分解的。
⾸先给⼤家介绍⼀个对于任意$m \times n$矩阵的更具普遍意义的⼀般性质:
对于⼀个$m \times n$ ,秩为 r 的矩阵 A,这⾥我们暂且假设 $m > n$,于是就有 $r \leq n < m$的不等关系。我们在$R^n$空间中⼀定可以找到⼀组标准正交向量$v_1, v_2, …, v_n$,在$R^m$空间中⼀定可以找到另⼀组标准正交向量$u_1, u_2, …, u_m$ ,使之满⾜ n 组相等关系: $Av_i = \sigma_i u_i$,其中(i 取 1~n)。
$Av_i = \sigma_i u_i$这个等式⾮常神奇,我们仔细地揭开⾥⾯的迷雾,展现它的精彩之处。
矩阵 A 是⼀个$m \times n$的矩阵,它所表⽰的线性变换是将 n 维原空间中的向量映射到更⾼维的 m 维⽬标空间中,而$Av_i = \sigma_i u_i$这个等式意味着,在原空间中找到⼀组新的标准正交向量$\begin{bmatrix}v_1, v_2, …, v_n\end{bmatrix}$ ,在⽬标空间中存在着对应的⼀ 组标准正交向量$\begin{bmatrix}u_1, u_2, …, u_n\end{bmatrix}$ ,此时$v_i$与$u_i$ 线性⽆关。
当矩阵 A 作⽤在原空间上的某个基向量 上时,其线性变换的结果就是:对应在⽬标空间中的$u_i$向量沿着⾃⾝⽅向伸⻓$\sigma_i$倍,并且任意⼀对$(v_i, u_i)$向量都满⾜这种关系(显然特征值分解是这⾥的⼀种特殊情况,即两组标准正交基向量相等)。
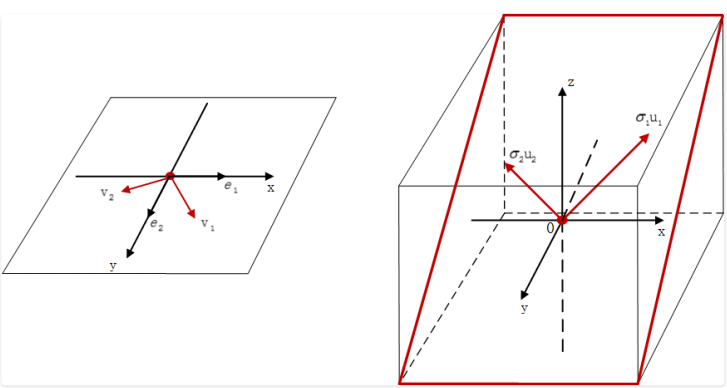
在$Av_i = \sigma_i u_i$的基础上,我们明⽩该如何往下走了:
\[A \begin{bmatrix}v_1 & v_2 & ... & v_n\end{bmatrix} = \begin{bmatrix}\sigma_1 u_1 & \sigma_2 u_2 & ... & \sigma_n u_n \end{bmatrix}\]转换成:
\[A \begin{bmatrix}v_1 & v_2 & ... & v_n\end{bmatrix} = \begin{bmatrix} u_1 & u_2 & ... & u_n \end{bmatrix}\begin{bmatrix}\sigma_1 & & & \\ & \sigma_2 & & \\ & & ... & \\ & & & \sigma_n\end{bmatrix}\]我们发现$u_{n+1}, u_{n+2}, …, u_m$并没有包含在式⼦⾥,我们把它们加进去,把$u_{n+1}, u_{n+2}, …, u_m$加到矩阵右侧,形成完整的 m 阶⽅阵:
\[U = \begin{bmatrix}u_1 & u_2 & ... & u_n & u_{n+1} & ... & u_m\end{bmatrix}\]在对⻆矩阵下⽅加上 m-n 个全零⾏,形成$m \times n$的矩阵:
\[\Sigma = \begin{bmatrix}\sigma_1 & & & \\ & \sigma_2 & & \\ & & ... & \\ & & & \sigma_n \\ & & & \\ & & &\end{bmatrix}\]由于$\Sigma$矩阵最下⾯的 m-n ⾏全零,因此右侧的计算结果不变,等式依然成⽴。
此时就有$AV = U\Sigma$ ,由于 V 的各列是标准正交向量,因此$V^{-1} = V^T$ ,移到等式右侧,得到了⼀个矩阵分解的式⼦:
\[A = U \Sigma V^T\]其中 U 和 V 是由标准正交向量构成的 m 阶和 n 阶⽅阵,而 是⼀个 的对⻆矩阵(注意,不是⽅阵)。
# 分析分解过程中的细节
此时还有⼀个最关键的地⽅似乎没有明确:就是⽅阵 U 和⽅阵 V 该如何取得,以及$\Sigma$矩阵中的各个值应该为多少,我们借助在对称矩阵那⼀讲中储备的基础知识来⼀⼀化解。
我们还是从$A = U \Sigma V^T$式⼦⼊⼿。⾸先,获取转置矩阵$A^T = (U \Sigma V^T)^T = V \Sigma U^T$ ,我们在此基础上可以获取两个对称矩阵
第⼀个对称矩阵是:
\[A^TA = V \Sigma U^T U \Sigma V^T\]由于 U 的各列是标准正交向量,因此$U^TU = I$ ,式⼦最终化简为了: $A^TA = V \Sigma^2 V^T$。
同理,第⼆个对称矩阵:
\[AA^T = U \Sigma V^T V \Sigma U^T = U \Sigma^2 U^T\]$A^TA$是 n 阶对称⽅阵, $AA^T$是 m 阶对称 ⽅阵。它们的秩相等,为$r = Rank(A)$ 。因此它们拥有完全相同的 r 个⾮零特征值,从⼤到小排列为$\lambda_1, \lambda_2, …, \lambda_r$ ,两个对称矩阵的剩余 n-r 个和 m-r 个特征值为 0。这进⼀步也印证了 $A^TA = V \Sigma^2 V^T$和$AA^T = U \Sigma^2 U^T$对⻆线上的⾮零特征值是完全⼀样的。
同时,由对称矩阵的性质可知: $A^TA$⼀定含有 n个标准正交特征向量,对应特征值从⼤到小的顺序排列为:$\begin{bmatrix}v_1 & v_2 & … & v_n\end{bmatrix}$ ,而$AA^T$也⼀定含有 m 个标准正交特征向量,对应特征值从⼤到小依次排列为$\begin{bmatrix}u_1 & u_2 & … & u_m\end{bmatrix}$。这⾥的$v_i$$u_i$和 ⼀⼀对应。
求出$AA^T$或$A^TA$的⾮零特征值,从⼤到小排列为:$\lambda_1, \lambda_2, …, \lambda_r$ , $\Sigma$矩阵中对⻆线上的⾮零值$\sigma_i$则依次为:$\sqrt{\lambda_1}, \sqrt{\lambda_2}, …, \sqrt{\lambda_r}$ 。因此, $\Sigma$矩阵对⻆线上$\sigma_r$以后的元素均为 0 了。
整个推导分析过程结束,我们隐去零特征值,最终得到了最完美的 SVD 分解结果.
\[A = \begin{bmatrix}u_1 & u_2 & ... & u_m\end{bmatrix} \begin{bmatrix}\sigma_1 & & & & \\ & \sigma_2 & & & \\ & & ... & & \\ & & & \sigma_r & \\ & & & & \\ & & & & \end{bmatrix} \begin{bmatrix}v_1^T \\ v_2^T \\ ... \\ v_n^T\end{bmatrix}\]我们⽤⼀个抽象图来⽰意⼀下分解的结果,有助于⼤家加深印象,如图所⽰:
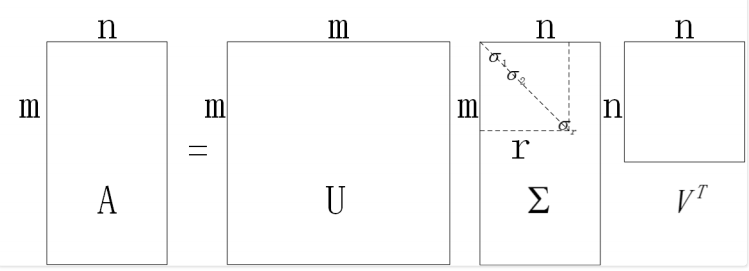
由此,我们顺利得到了任意$m \times n$矩阵 A 的 SVD 分解形式。如