最优化问题
最优化问题由两部分组成:
\[minimize f(x)\] \[\text{subject to } x \in \Omega\]它要解决的实际问题就是,针对我们上⾯所写的实值函数 f,去寻找⼀个合适的 x,使得函数 f 的取值达到最小,需要注意的 是,如果函数 f 是⼀个⼀元函数,那么 x 就是⼀个使得函数取得最小值的数值,而对于⼀个 n 元函数 f 而⾔,⾃然的,x 就是⼀个 n 维向量:$\begin{bmatrix}x_1 & x_2 & x_3 & … & x_n\end{bmatrix}^T$。
我们对应回忆⼀下⼆元函数 f(x,y) 的情形,实际上我们就是在这⾥把⾃变量 x 和 y 统⼀表述成向量$\begin{bmatrix}x_1 & x_2\end{bmatrix}^T$。
我们知道所有n维向量会构成一个$R^n$空间, 所谓的集合$\Omega$是自变量x的约束集, 在空间中, 也是$R^n$空间中的一个子集, 一般我们将约束集表示成:
\[\Omega = x : h(x) = 0, g(x) \leq 0\]换句话说, 我们所讨论的有约束条件的优化问题,就是指⾃变量 x 必须取⾃于约束集$\Omega$范围中的值,在这个范围内寻找使得 函数 f 取得极小值的 x 的取值。
当然,如果我们的约束集定义为$\Omega = R^n$,实际上就对应了另⼀种情况,也就是⽆约束的优化问题。
在实际问题中,我们可能还会想到要求取⽬标函数 f 的极⼤值,我们对其取负号 -f,就将其统⼀到求极小值的框架中来了。
关于极小值的一些概念
对于在约束域$\Omega$内的点$x^$,如果在约束域内它的邻域$\mid x - x^ \mid < \epsilon$当中,对于其余所有的⾃变量 x,都有$f(x) \geq f(x^)$,那么我们就说$x^$是函数约束域中的⼀个局部极小值点;那么如果在整个约束域$\Omega$中的自变量 x 都满足$f(x) \geq f(x^)$,那么此时的$x^$就由局部极小值点升格成了全局极小值点。
我们以⼀个最简单的⼀元函数 y=f(x) 的图像为例:
![[[[1599989885171]]]](https://markdown.xiaoshujiang.com/img/spinner.gif)
在这个例⼦中,图像上所展⽰的是函数 f(x) 在约束域内的图像,很显然$x = x_1$以及$x = x_2$都是极小值点,而进⼀步的, $x_1$是全局极小值点,$x_2$是局部极小值点。
剖析最优化分析的工具
我们以⼆元函数$f(x_1, x_2) = x_1^2 + 3x_2^2 + 2x_1x_2 + 4x_1 + 5x_2$为例。
函数 f 的⼀阶导数$D_f$是⼀个向量,它和梯度向量⼀致,即:
\[D_f = \begin{bmatrix} \frac{\partial f}{\partial x_1} & \frac{\partial f}{\partial x_2} & \cdots & \frac{\partial f}{\partial x_n} \end{bmatrix}\]在上面的例子中:
\[D_f = \begin{bmatrix}2x_1 + 2x_2 + 4 & 2x_1 + 6x_2 + 5\end{bmatrix}\]而函数的二阶导数$D^2f$将组成一个矩阵, 这就是海森(Hessian)矩阵。
\[D^2 f = \begin{bmatrix} \frac{\partial^2 f}{\partial x_1^2} & \frac{\partial^2 f}{\partial x_1 x_2} & \cdots & \frac{\partial^2 f}{\partial x_1 x_n} \\ \cdots & \cdots & \cdots & \cdots \\ \frac{\partial^2 f}{\partial x_n x_1} & \frac{\partial^2 f}{\partial x_n x_2} & \cdots & \frac{\partial^2 f}{\partial x_n^2} \\ \end{bmatrix}\]进⼀步对应的,上⾯的⼆元函数$f(x_1, x_2)$的海森矩阵为$\begin{bmatrix}2 & 2 \ 2 & 6\end{bmatrix}$。
探索极小值存在的条件
一阶必要条件
我们来看下⾯这个简单的例子$f(x_1, x_2) = x_1^2 + x_2^2$ ,我们观察它在极小值点 (0,0) 处的图像:
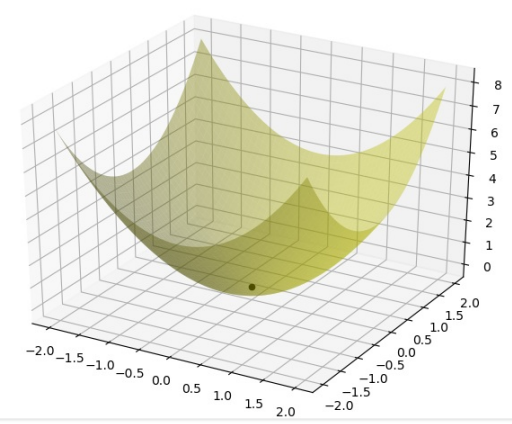
很显然,函数 f 在极小值点$x^$邻域附近的点 x 的取值需要满足$f(x) \geq f(x^)$ ,也就是说在取值点$x^*$处沿着各个方向向量 u 的导数都应该大于等于 0:
\[\lim_{h \rightarrow 0} \frac{f(p + hu) - f(p)}{h} = \nabla f(p) · u \geq 0\]思考: 为什么?
回答: 因为它附近的值都大于它, 所以往任何方向走都应该是是正的, 也就是说梯度和方向向量的点乘大于等于0.
由于我们的方向导数在任意方向上都满足大于等于 0,因此沿着 -u ⽅向,这个不等关系依然成立,也 就是说我们需要同时满足以下两个不等式:
\[\nabla f(p)·u \geq 0\] \[\nabla f(p) · (-u) \geq 0 \Rightarrow \nabla f(p) · u \leq 0\]那么显然$\nabla f(p) · u = 0$对于任意方向向量u都成立, 因此只能满足: $\nabla f(p) = 0$。
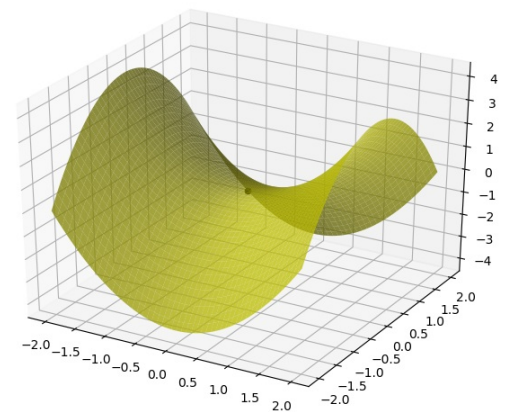
但是请注意, $\nabla f(p) = 0$只是满足极小值存在的一个必要条件, 我们可以看看另外⼀个例⼦:$f(x_1, x_2) = x_1^2 - x_2^2$的图像,它在点 p=(0,0) 处,也满足$\nabla f(p) = 0$ ,但是从图上看,它显然不是⼀个极小值点:
二阶必要条件
那我们继续探索,看看为了保证极值点存在,⼆阶导,也就是海森矩阵应该满足的条件:
我们回忆⼀下多元函数的⼆阶泰勒近似时曾经讲过的内容:
\[f(x, y) = f(x_0, y_0) + \begin{bmatrix}\frac{\partial f}{\partial x}(x_0, y_0) & \frac{\partial f}{\partial y}(x_0, y_0)\end{bmatrix}\begin{bmatrix}x - x_0 \\ y - y_0\end{bmatrix} + \frac{1}{2}\begin{bmatrix}x - x_0 & y - y_0\end{bmatrix}\begin{bmatrix}\frac{\partial^2 f}{\partial x^2}(x_0, y_0) & \frac{\partial f^2}{\partial x \partial y}(x_0, y_0) \\ \frac{\partial f^2}{\partial x \partial y}(x_0, y_0) & \frac{\partial f^2}{\partial y^2}(x_0, y_0) \end{bmatrix}\begin{bmatrix}x - x_0 \\ y - y_0\end{bmatrix} + R_2(x - x_0, y - y_0)\]其中, $R_2$表示的余项是一个高阶小量, 在$(x, y) \rightarrow (x_0, y_0)$时, $R_2 \rightarrow 0$。
我们把上面的式子,按照极小值点$x^$处的梯度$\nabla f(x^)$和海森矩阵$\nabla^2 f(x^)$进行符号化表示,并且进行一般化,x 表示一般化的多元自变量$\begin{bmatrix}x_1 & x_2 & … & x_n\end{bmatrix}$ , $x^$表示的就是极小值点:
\[f(x^* + \Delta x) = f(x^*) + (\Delta x)^T \nabla f(x^*) + \frac{1}{2} (\Delta x)^T \nabla^2f(x^*)(\Delta x) + R_2(\Delta x)\]如果满足$x^$是函数的极小值, 那么依据上面所述的一阶必要条件可知$\nabla f(x^) = 0$, 我们进一步整理:
\[f(x^* + \Delta x) - f(x^*) = \frac{1}{2} (\Delta x)^T \nabla^2 f(x^*)(\Delta x) + R_2(\Delta x) \geq 0\]由于当$\Delta x \rightarrow 0$时, 余项$R_2(x) \rightarrow 0$, 因此此时需要满足:
\[f(x^* + \Delta x) - f(x^*) = \frac{1}{2}(\Delta x)^T \nabla^2 f(x^*)(\Delta x) \geq 0\]即:$(\Delta x)^T \nabla^2 f(x^*) (\Delta x) \geq 0$对于任意向量$\Delta x$都成立, 由于海森矩阵是对称矩阵, 因此这个结论也可描述为:
如果$x^$是函数的极小值点,那么$x^$处的海森矩阵是⼀个半正定的矩阵。
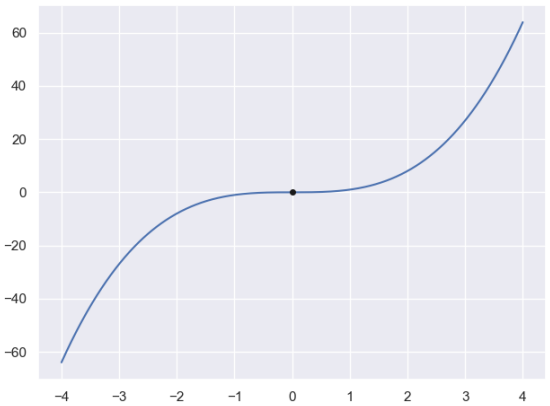
当然,这个条件也是必要非充分的,举个最简单的⼀元函数的反例: $y = x^3$,在 x=0 点处,它同时满足一阶导数 f’(x) 为 0,二阶导数 f’‘(x) 非负(一元函数的二阶导数就是海森矩阵退化后的情况)。 但是从下面的图中我们很轻松地看出,x=0 显然不是$y = x^3$的极小值点:
⼆阶充分条件
如果点$x^*$处同时满足一阶和二阶的如下条件:
\[\nabla f(x^*) = 0\] \[(\Delta x)^T \nabla^2 f(x^*) (\Delta x) > 0\]这⾥的不等关系变成了单纯的大于 0, 处的海森矩阵由半正定变成了正定。
只要满足上面的条件,就能在$\Delta x \rightarrow 0$的邻域内保证:
\[f(x^* + \Delta x) - f(x^*) = (\Delta x)^T f(x^*) + \frac{1}{2} (\Delta x)^T \nabla^2 f(x^*)(\Delta x) = 0 + \frac{1}{2}(\Delta x)^T \nabla^2 f(x^*)(\Delta x) > 0\]在任意方向上都成立。
因此,函数 f 在$x^$处同时满足$\nabla f(x^) = 0$且海森矩阵正定,是$x^*$严格极小的充分条件。
总结
- 一阶必要条件: $\nabla f(x^*) = 0$
- 二阶必要条件:$\Delta x \nabla^2 f(x^*) \Delta x \geq 0$
- 二阶充分条件:$\Delta x \nabla^2 f(x^*) \Delta x > 0$