由NFL定理可知,机器学习貌似 是不可行的。但是,随后引入了统计学知识,如果样本数据足够大,且hypothesis个 数有限,那么机器学习一般就是可行的。
回顾:
NFL定理:在D以外的数据中更接近目标函数似乎是做不到的。 NFL定理表明没有一个学习算法可以在任何领域总是产生最准确的学习器。 平常一个学习算法比另一个算法更好, 只是针对特定的问题, 特定的先验信息, 数据的分布, 训练样本的数目, 代价或奖励函数等。
Recap and Preview
我们先来看一下基于统计学的机器学习流程图:
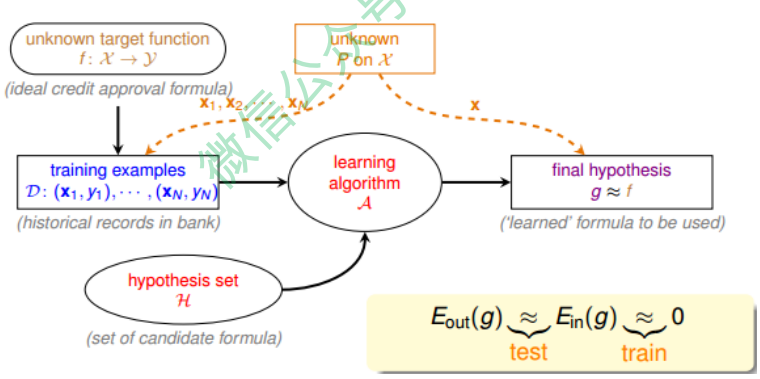
该流程图中,训练样本D和最终测试h的样本都是来自同一个数据分布,这是机器能够学习的前提。另外,训练样本D应该足够大,且hypothesis set的个数是有限的,这样根据霍夫丁不等式,才不会出现Bad Data,保证$E_{in} \approx E_{out}$,即有很好的泛化能 力。同时,通过训练,得到使$E_{in}$最小的h,作为模型最终的g,g接近于目标函数。
第一节课,我们介绍了机器学习的定义, 目标是找出最好的g,使$g \approx f$,保证$E_{out}(g) \approx 0$;
第二节课,我们介绍了如何让$E_{in} \approx 0$, 可以使用PLA、pocket等演算法来实现;
第三节课,我们介绍了机器学习 的分类,我们的训练样本是批量数据(batch),处理监督式(supervised)二元分类 (binary classification)问题;
第四节课,我们介绍了机器学习的可行性,通过统计学知识,把$E_{in}(g)$与$E_{out}(g)$联系起来,证明了在一些条件假设下,$E_{in}(g) \approx E_{out}(g)$ 成立。

这四节课总结下来,我们把机器学习的主要目标分成两个核心的问题:
- $E_{in}(g) \approx E_{out}(g)$
- $E_{in}(g)$足够小
上节课介绍的机器学习可行的一个条件是hypothesis set的个数M是有限的,那M跟上 面这两个核心问题有什么联系呢?
我们先来看一下,当M很小的时候,由上节课介绍的霍夫丁不等式,得到$E_{in}(g) \approx E_{out}(g)$, 即能保证第一个核心问题成立。
但M很小时,演算法A可以选择 的hypothesis有限,不一定能找到使$E_{in}(g)$足够小的hypothesis,即不能保证第二个核心问题成立。
当M很大的时候,同样由霍夫丁不等式, $E_{in}(g)$与$E_{out}(g)$的差距可 能比较大,第一个核心问题可能不成立。
而M很大,使的演算法A的可以选择的 hypothesis就很多,很有可能找到一个hypothesis,使$E_{in}(g)$足够小,第二个核心问 题可能成立。

从上面的分析来看,M的选择直接影响机器学习两个核心问题是否满足,M不能太大也不能太小。那么如果M无限大的时候,是否机器就不可以学习了呢?例如PLA算法 中直线是无数条的,但是PLA能够很好地进行机器学习,这又是为什么呢?如果我们能将无限大的M限定在一个有限的$m_H$内,问题似乎就解决了。

这里的意思是我们能接受的坏事情发生的概率$\delta$最大是0.05, 然后计算所需要的N。
Effective Number of Line
我们先看一下上节课推导的霍夫丁不等式:
\[P[\mid E_{in}(g) - E_{out}(g) \mid > \epsilon] \leq 2 · exp(-2 \epsilon^2 N)\]其中,M表示hypothesis的个数。每个hypothesis下的BAD events $B_m$级联的形式满 足下列不等式:
\[P[B_1 or B_2 or \cdots or B_M] \leq P[B_1] + P[B_2] + \cdots + P[B_M] \leq 2 M exp(-2 \epsilon^2 N)\]当$M = \infty$时, 上面不等式右边值将会很大,似乎说明BAD events很大, $E_{in}(g)$与$E_{out}(g)$也并不接近。但是BAD events $B_m$级联的形式实际上是扩大了上界,union bound过大。这种做法假设各个hypothesis之间没有交集,这是最坏的情况,可是实际 上往往不是如此,很多情况下,都是有交集的,也就是说M实际上没那么大,如下图 所示:
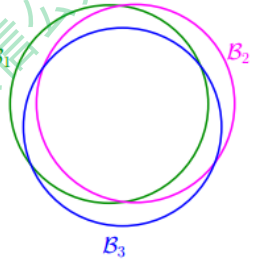
也就是说union bound被估计过高了(over-estimating)。所以,我们的目的是找出不 同BAD events之间的重叠部分,也就是将无数个hypothesis分成有限个类别。
如何将无数个hypothesis分成有限类呢?我们先来看这样一个例子,假如平面上用直线将点分开,也就跟PLA一样。如果平面上只有一个点x1,那么直线的种类有两种: 一种将x1划为+1,一种将x1划为-1:
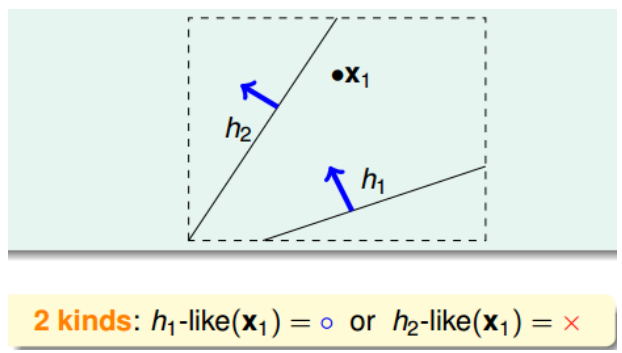
如果平面上有两个点x1、x2,那么直线的种类共4种:x1、x2都为+1,x1、x2都 为-1,x1为+1且x2为-1,x1为-1且x2为+1:
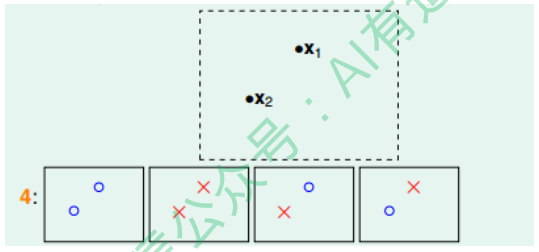
如果平面上有三个点x1、x2、x3,那么直线的种类最多8种:
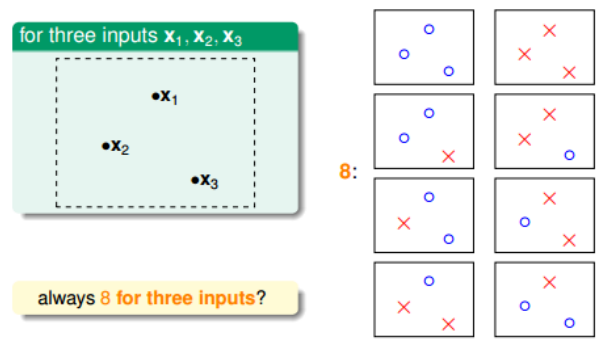
但是,在三个点的情况下,也会出现不能用一条直线划分的情况:
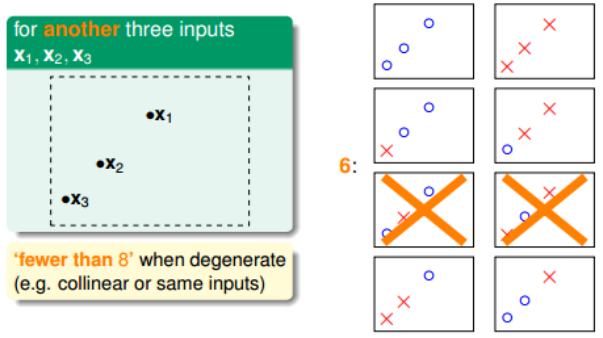
也就是说,对于平面上三个点,不能保证所有的8个类别都能被一条直线划分。那如果 是四个点x1、x2、x3、x4,我们发现,平面上找不到一条直线能将四个点组成的16个 类别完全分开,最多只能分开其中的14类,即直线最多只有14种:
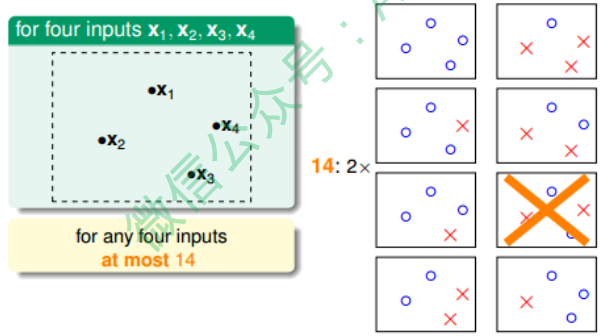
经过分析,我们得到平面上线的种类是有限的,1个点最多有2种线,2个点最多有4种 线,3个点最多有8种线,4个点最多有14($< 2^4$)种线等等。我们发现,有效直线的数量总是满足$\leq 2^N$,其中,N是点的个数。所以,如果我们可以用effective(N)代替 M,霍夫丁不等式可以写成:
\[P[\mid E_{in}(g) - E_{out}(g) \mid > \epsilon] \leq 2 · effective(N)· exp(-2 \epsilon^2 N)\]已知$effective < 2^N$, 如果能够保证$effective(N) « 2^N$, 即不等式右边接近于零,那 么即使M无限大,直线的种类也很有限,机器学习也是可能的。

Effective Number of Hypotheses
接下来先介绍一个新名词:二分类(dichotomy)。dichotomy就是将空间中的点(例如二维平面)用一条直线分成正类(蓝色o)和负类(红色x)。令H是将平面上的点 用直线分开的所有hypothesis h的集合,dichotomy H与hypotheses H的关系是:hypotheses H是平面上所有直线的集合,个数可能是无限个,而dichotomy H是平面上能将点完全用直线分开的直线种类,它的上界是$2^N$。接下来,我们要做的就是尝试 用dichotomy代替M。

成长函数(growth function),记为$m_H(H)$。成长函数的定义是:对于由N个点组成的不同集合中,某集合对应的dichotomy最大,那么这个dichotomy值就是$m_H(H)$,它的上界是$2^N$:
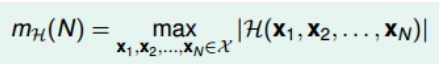
成长函数其实就是我们之前讲的effective lines的数量最大值。根据成长函数的定义, 二维平面上, $m_H(H)$随N的变化关系是:
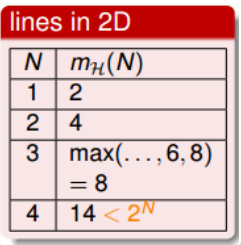
接下来,我们讨论如何计算成长函数。先看一个简单情况,一维的Positive Rays:

若有N个点,则整个区域可分为N+1段,很容易得到其成长函数$m_H(N) = N + 1$。 注意当N很大时, $(N + 1) « 2^N$,这是我们希望看到的。
另一种情况是一维的Positive Intervals:

它的成长函数可以由下面推导得出:

思考: 怎么推导的?
这种情况下,$m_H(N) = \frac{1}{2}N^2 + \frac{1}{2}N + 1 « 2^N$ ,在N很大的时候,仍然是满足的。
再来看这个例子,假设在二维空间里,如果hypothesis是凸多边形或类圆构成的封闭 曲线,如下图所示,左边是convex的,右边不是convex的。那么,它的成长函数是多少呢?
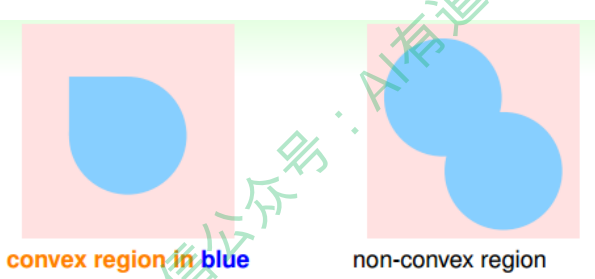
当数据集D按照如下的凸分布时,我们很容易计算得到它的成长函数$m_H = 2^N$。这 种情况下,N个点所有可能的分类情况都能够被hypotheses set覆盖,我们把这种情形 称为shattered。也就是说,如果能够找到一个数据分布集,hypotheses set对N个输 入所有的分类情况都做得到,那么它的成长函数就$2^N$ 。
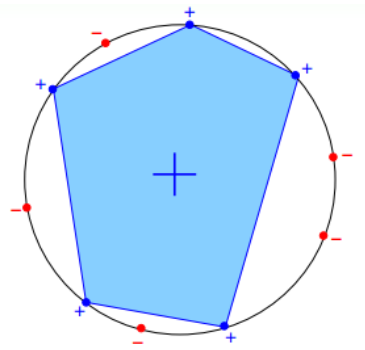
Break Point

其中,positive rays和positive intervals的成长函数都是polynomial的,如果用$m_H$代替M的话,这两种情况是比较好的。而convex sets的成长函数是exponential的,即等 于M,并不能保证机器学习的可行性。
对于2D perceptrons,我们之前分析了3个点,可以做出8种所有的dichotomy,而4个点,就无法做出所有16个点的dichotomy了。所以,我们就把4称为2D perceptrons的 break point(5、6、7等都是break point)。令有k个点,如果k大于等于break point 时,它的成长函数一定小于2的k次方。
根据break point的定义,我们知道满足$m_H(k) \neq 2^k$的k的最小值就是break point。 对于我们之前介绍的四种成长函数,他们的break point分别是:

通过观察,我们猜测成长函数可能与break point存在某种关系:对于convex sets,没 有break point,它的成长函数是2的N次方;对于positive rays,break point k=2,它 的成长函数是O(N);对于positive intervals,break point k=3,它的成长函数是$O(N^2)$。则根据这种推论,我们猜测2D perceptrons,它的成长函数$m_H(N) = O(N^{k-1})$。如果成立,那么就可以用$m_H$代替M,就满足了机器能够学 习的条件。