线性回归问题
在之前的Linear Classification课程中,讲了信用卡发放的例子,利用机器学习来决定 是否给用户发放信用卡。本节课仍然引入信用卡的例子,来解决给用户发放信用卡额度的问题,这就是一个线性回归(Linear Regression)问题。

令用户特征集为d维的$X$,加上常数项,维度为$d+1$,与权重$w$的线性组合即为Hypothesis, 记为$h(x)$。线性回归的预测函数取值在整个实数空间,这跟线性分类不同。
\[h(x) = w^T X\]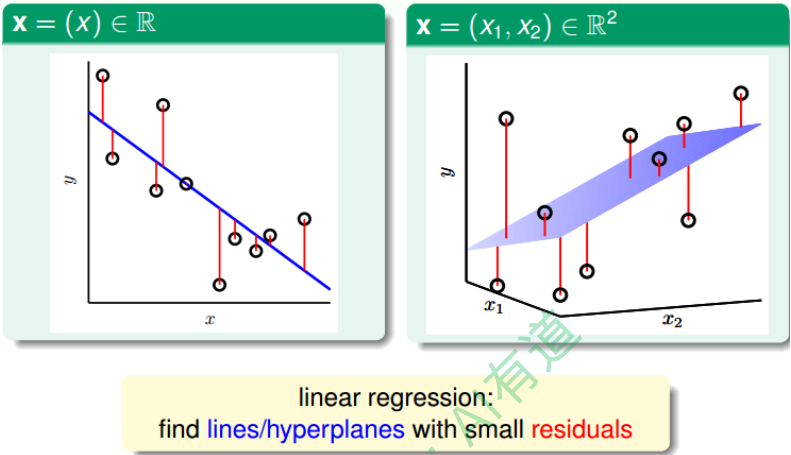
根据上图,在一维或者多维空间里,线性回归的目标是找到一条直线(对应一维)、 一个平面(对应二维)或者更高维的超平面,使样本集中的点更接近它,也就是残留误差Residuals最小化。
一般最常用的错误测量方式是基于最小二乘法,其目标是计算误差的最小平方和对应 的权重w,即squared error:

线性回归算法
样本数据误差$E_{in}$是权重$w$的函数,因为$X$和$y$都是已知的。我们的目标就是找出合适的$w$ ,使$E_{in}$能够最小。那么如何计算呢?
首先,运用矩阵转换的思想,将$E_{in}$计算转换为矩阵的形式。
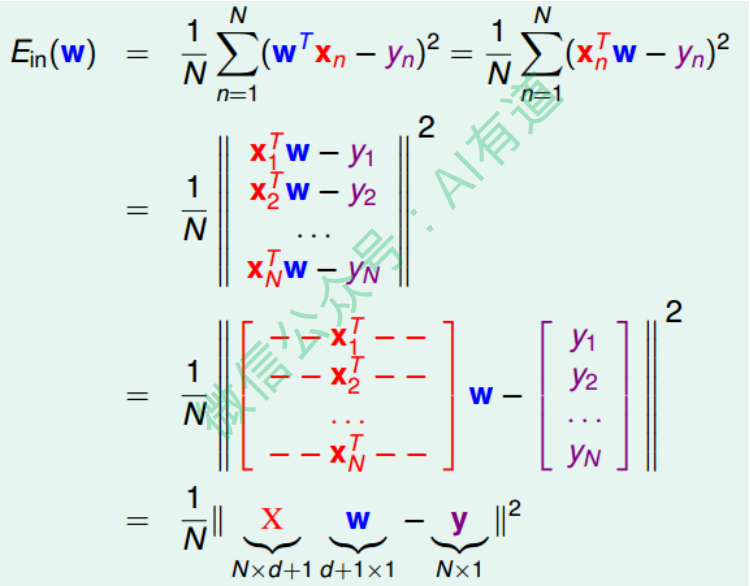
然后,对于此类线性回归问题, $E_{in}(w)$一般是个凸函数。凸函数的话,我们只要找到一阶导数等于零的位置,就找到了最优解。那么,我们将$E_{in}(w)$对每个$w_i, i = 0, 1, \cdots , d$求偏导,偏导为零的$w_i$,即为最优化的权重值分布。

根据梯度的思想,对$E_w$进行矩阵化求偏导处理:
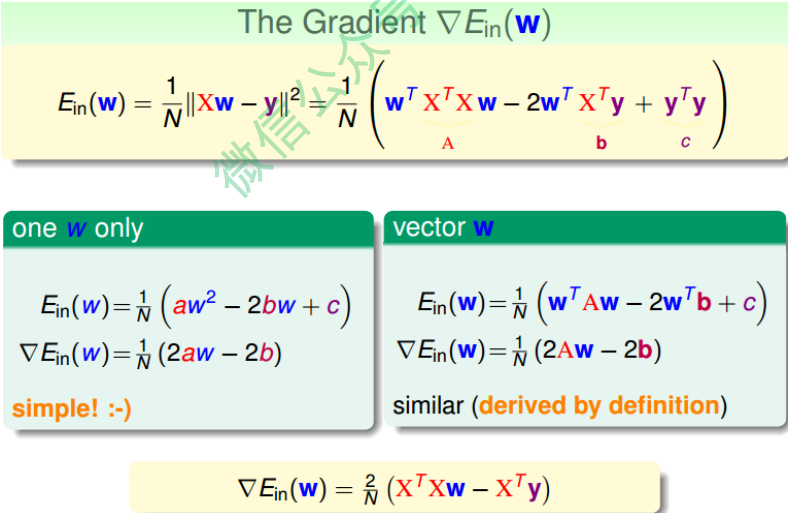
令偏导为零,最终可以计算出权重向量$w$为:

最终,我们推导得到了权重向量$w = (X^T X)^{-1} X^Ty$,这是closed-form 解。其中, $(X^TX)^{-1}X^T$又称为伪逆矩阵pseudo-inverse,记为$X^+$,维度是 $(d+1)\times N$。
但是,我们注意到,伪逆矩阵中有逆矩阵的计算,逆矩阵$(X^TX)^{-1}$是否一定存在?一 般情况下,只要满足样本数量N远大于样本特征维度d+1,就能保证矩阵的逆是存在 的,称之为非奇异矩阵。但是如果是奇异矩阵,不可逆怎么办呢?其实,大部分的计 算逆矩阵的软件程序,都可以处理这个问题,也会计算出一个逆矩阵。所以,一般伪 逆矩阵是可解的。
泛化问题
这种求解权重向量的方法是机器学习吗?或者说这 种方法满足我们之前推导VC Bound,即是否泛化能力强$E_{in} \approx E_{out}$?

有两种观点:1、这不属于机器学习范畴。因为这种closed-form解的形式跟一般的机器 学习算法不一样,而且在计算最小化误差的过程中没有用到迭代。2、这属于机器学习范畴。因为从结果上看, $E_{in}$和$E_{out}$都实现了最小化,而且实际上在计算逆矩阵的过程中,也用到了迭代。
其实,只从结果来看,这种方法的确实现了机器学习的目的。下面通过介绍一种更简 单的方法,证明linear regression问题是可以通过线下最小二乘法方法计算得到好的$E_{in}$和$E_{out}$的。
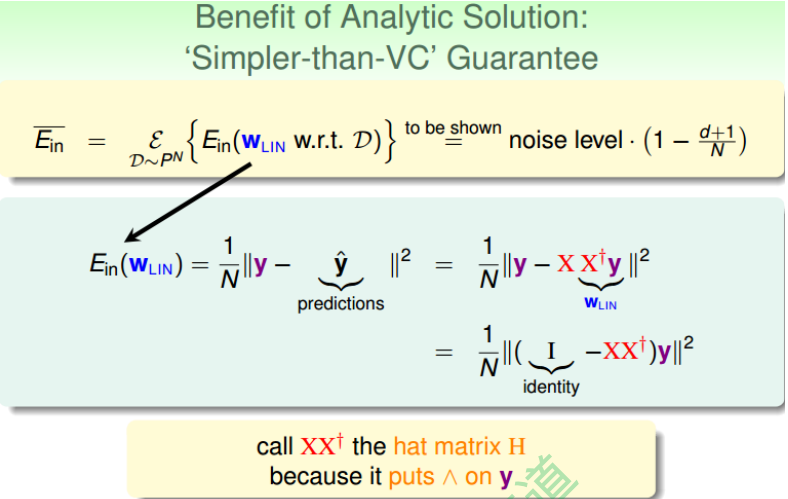
首先,我们根据平均误差的思想,把$E_{in}(w_{LIN})$写成如图的形式,经过变换得到:
\[E_{in}(w_{LIN}) = \frac{1}{N}\|(I - XX^+)y \|^2 = \frac{1}{N}\|(I - H)y\|^2\]我们称$XX^+$为帽子矩阵,用H表示。
下面从几何图形的角度来介绍帽子矩阵H的物理意义。
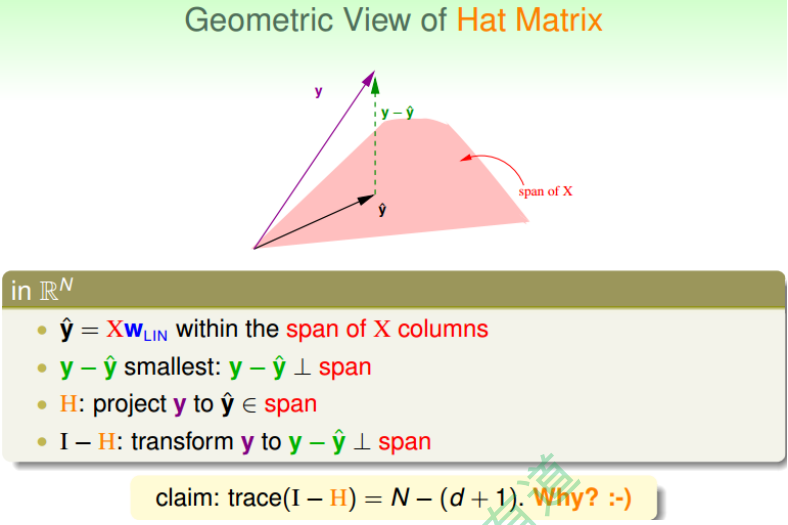
图中,y是N维空间的一个向量,粉色区域表示输入矩阵X乘以不同权值向量w所构成的 空间,根据所有w的取值,预测输出都被限定在粉色的空间中。向量$\hat y$就是粉色空间中 的一个向量,代表预测的一种。y是实际样本数据输出值。
机器学习的目的是在粉色空间中找到一个$\hat y$,使它最接近真实的y,那么我们只要将y在粉色空间上作垂直投影即可,投影得到的$\hat y$即为在粉色空间内最接近y的向量。这样即使平均误差$\bar E$最小。
从图中可以看出, $\hat y$是y的投影,已知$\hat y = H y$ ,那么H表示的就是将y投影到$\hat y$的一种操作。图中绿色的箭头$y - \hat y$是向量y与$\hat y$相减, 垂直于粉色区域。已知$(I - H)y = y - \hat y$那么$I-H$表示的就是将y投影到$y - \hat y$即垂直于粉色区域的一种操作。这样的话,我们就赋予了$H$和$I-H$不同但又有联系的物理意义。
这里$trace(I-H)$称为IH的迹,值为$N-(d+1)$。这条性质很重要,一个矩阵的$trace$等于该矩阵的所有特征值(Eigenvalues)之和。下面给出简单证明:
\[\begin{aligned} trace(I - H) &= trace(I) - trace(H) \\ &= N - trace(XX^+) = N - trace(X(X^TX)^{-1}X^T) \\ &= N - trace(X^T X (X^T X)^{-1}) = N - trace(I_{d+1}) \\ &= N - (d + 1) \end{aligned}\]介绍下该$I-H$这种转换的物理意义:原来有一个有N个自由度的向量y,投影到一个有 d+1维的空间x(代表一列的自由度,即单一输入样本的参数,如图中粉色区域),而余数剩余的自由度最大只有$N-(d+1)$种。
在存在noise的情况下,上图变为:

图中,粉色空间的红色箭头是目标函数f(x),虚线箭头是noise,可见,真实样本输出y 由f(x)和noise相加得到。由上面推导, 已知向量y经过$I-H$转换为$y - \hat y$,而noise与y是线性变换关系,那么根据线性函数知识,我们推导出noise经过$I-H$也能转换为$y - \hat y$。则对于样本平均误差,有下列推导成立:
\[E_{in}(w_{LIN}) = \frac{1}{N}\|y - \hat y\|^2 = \frac{1}{N} \|(I - H) noise\|^2 = \frac{1}{N}(N - (d + 1))\|noise\|^2\]即
\[\bar E_{in} = noiselevel * (1 - \frac{d+1}{N})\]同样, 对$E_{out}$由如下结论
\[\bar E_{out} = noiselevel * (1 + \frac{d+1}{N})\]这个证明有点复杂,但是我们可以这样理解: $\bar E_{in}$与$\bar E_{out}$形式上只差了$\frac{(d + 1)}{N}$项,从哲学上来说,$\bar E_{in}$ 是我们看得到的样本的平均误差,如果有noise,我们把预测往noise那边偏一点,让$\bar E_{in}$好看一点点,所以减去$\frac{(d + 1)}{N}$项。那么同时,新的样本$\bar E_{out}$是我们看 不到的,如果noise在反方向,那么$\bar E_{out}$就应该加上$\frac{(d+1)}{N}$项。
我们把$\bar E_{in}$与$\bar E_{out}$画出来,得到学习曲线:
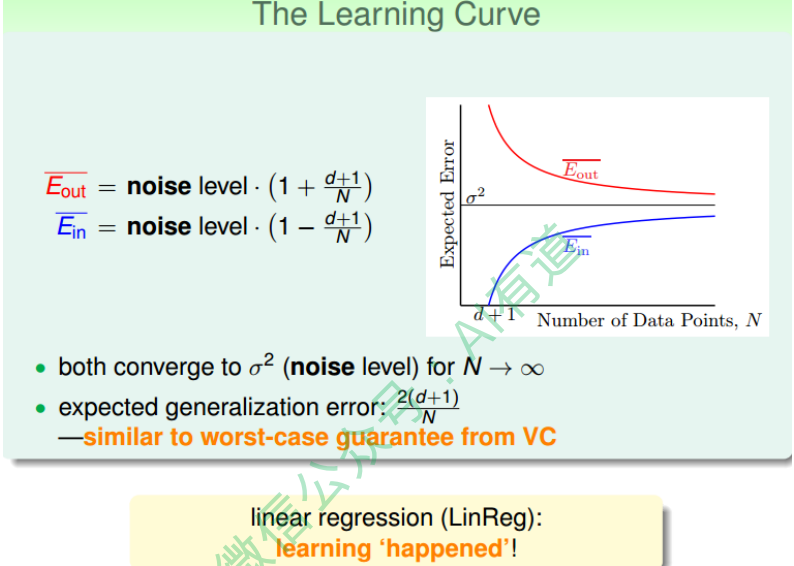
当N足够大时, $\bar E_{in}$与$\bar E_{out}$逐渐接近,满足$\bar E_{in} \approx \bar E_{out}$,且数值保持在noise level。 这就类似VC理论,证明了当N足够大的时候,这种线性最小二乘法是可以进行机器学 习的,算法有效!
Linear Regression方法解决Linear Classification问题

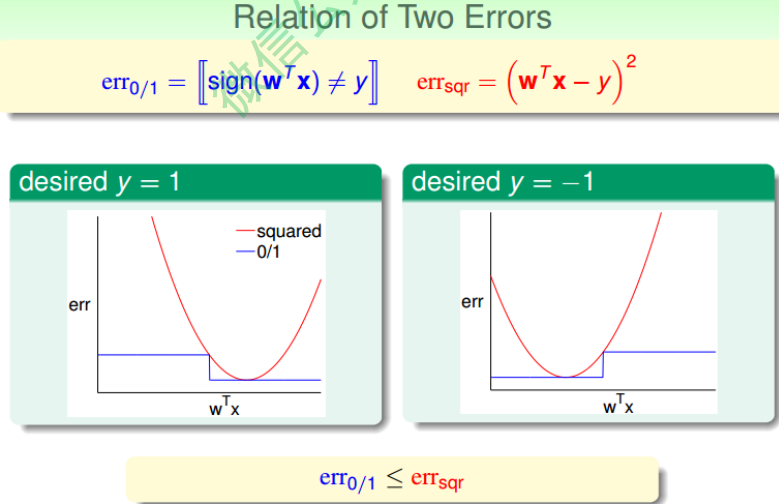
下图展示了两种错误的关系,一般情况下,squared error曲线在0/1 error曲线之上。即$err {0/1} \leq err{sqr}$。
根据之前的VC理论, $E_{out}$的上界满足:

从图中可以看出,用$err_{sqr}$代替$err_{0/1}$, $E_{out}$仍然有上界, 只不过是上界变得宽松 了。也就是说用线性回归方法仍然可以解决线性分类问题,效果不会太差。二元分类 问题得到了一个更宽松的上界,但是也是一种更有效率的求解方式。