Linear Models for Binary Classification
之前介绍几种线性模型都有一个共同点,就是都有样本特征x的加权运算,我们引入一 个线性得分函数s:
\[s = w^T x\]三种线性模型,第一种是linear classification。线性分类模型的hypothesis为$h(x) = sign(s)$, 取值范围为{-1,+1}两个值,它的err是0/1的,所以对应的$E_{in}(w)$是离散的,并不好解,这是个NP-hard问题。
第二种是linear regression。线性回归模型 的hypothesis为$h(x) = s$,取值范围为整个实数空间,它的err是squared的,所以对应的$E_{in}(w)$是开口向上的二次曲线,其解是closed-form的,直接用线性最小二乘法求解即可。
第三种是logistic regression。逻辑回归模型的hypothesis为$h(x) = \theta(s)$,取值范围为(-1,1)之间,它的err是cross-entropy的,所有对应的$E_{in}(w)$是平滑的凸函数,可以使用梯度下降算法求最小值。
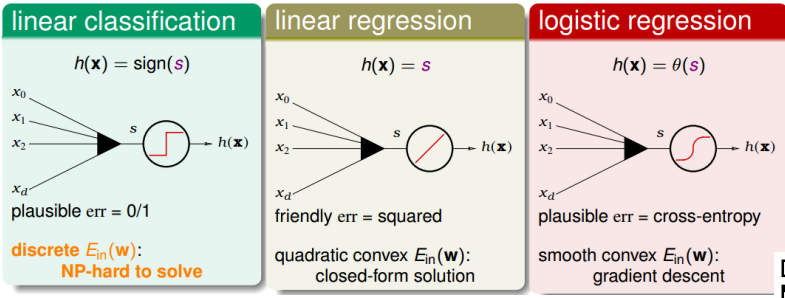
从上图中,我们发现,linear regression和logistic regression的error function都有最小 解。那么可不可以用这两种方法来求解linear classification问题呢?下面,我们来对这 三种模型的error function进行分析,看看它们之间有什么联系。
对于linear classification,它的error function可以写成:
\[err_{0/1}(s, y) = \mid sign(s) \neq y \mid = \mid sign(ys) \neq 1 \mid\]对于linear regression, 它的error function可以写成:
\[err_{SQR}(s, y) = (s - y)^2 = (ys - 1)^2\]对于logistics regression, 它的error function可以写成:
\[err_{CE}(s, y) = ln(1 + exp(-ys))\]上述三种模型的error function都引入了ys变量,那么ys的物理意义是什么?ys就是指 分类的正确率得分,其值越大越好,得分越高。
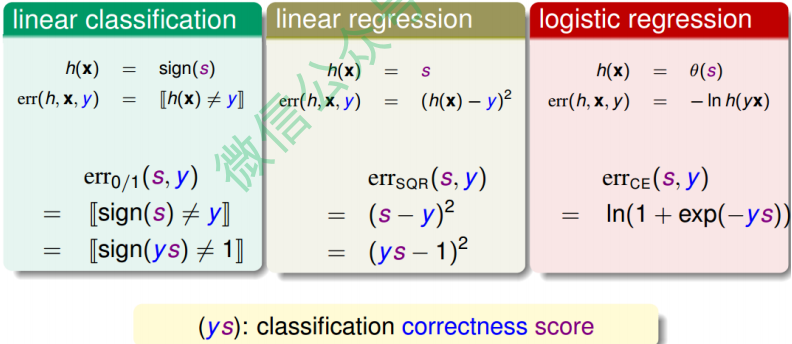
下面,我们用图形化的方式来解释三种模型的error function到底有什么关系:

从上图看出, ys是横坐标轴, $err_{0/1}$是呈阶梯状的, 在$ys > 0$时, $err_{0/1}$恒取最小值0.
$err_{SQR}$呈抛物线形式, 在$ys = 1$时, 取最小值, 且在$ys = 1$左右很小的区域内, $err_{0/1}$和$err_{SQR}$近似。 $err_{CE}$是呈指数下降的单调函数, ys越大, 其值越小。 同样在ys=1左右很小区域内, $err_{0/1}$和$err_{CE}$近似。 但是我们发现$err_{CE}$并不是始终在$err_{0/1}$上, 所以为了计算讨论方便, 我们把$err_{CE}$做幅值上的调整, 引入$err_{SCE} = log_2(1 + exp(-ys)) = \frac{1}{ln2}err_{CE}$, 这样能保证$err_{SCE}$始终在$err_{0/1}$上面, 如下图所示:

由上图可以看出:
\[err_{0/1}(s, y) \leq err_{SCE}(s, y) = \frac{1}{ln2}err_{CE}(s, y)\] \[E_{in}^{0/1}(w) \leq E_{in}^{SCE}(w) = \frac{1}{ln2} E_{in}^{CE}(w)\] \[E_{out}^{0/1}(w) \leq E_{out}^{SCE}(w) = \frac{1}{ln2} E_{out}^{CE}(w)\]那么由VC理论可以知道:
从0/1出发:
\[E_{out}^{0/1}(w) \leq E_{in}^{0/1}(w) + \Omega^{0/1} \leq \frac{1}{ln2} E_{in}^{CE}(w) + \Omega^{0/1}\]从CE出发:
\[E_{out}^{0/1}(w) \leq \frac{1}{ln2} E_{out}^{CE}(w) \leq \frac{1}{ln2}E_{in}^{CE}(w) + \frac{1}{ln2} \Omega^{CE}\]
问题: 这里的$\Omega$指什么?
通过上面的分析,我们看到err 0/1是被限定在一个上界中。这个上界是由logistic regression模型的error function决定的。而linear regression其实也是linear classification的一个upper bound,只是随着sy偏离1的位置越来越远,linear regression的error function偏差越来越大。综上所述,linear regression和logistic regression都可以用来解决linear classification的问题。
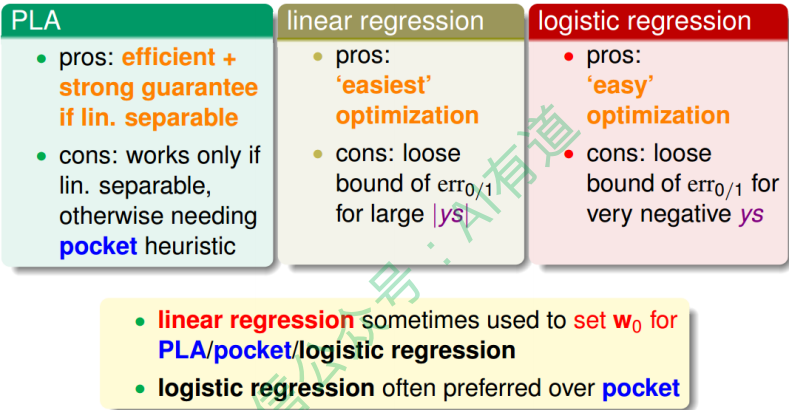
下图列举了PLA、linear regression、logistic regression模型用来解linear classification问题的优点和缺点。通常,我们使用linear regression来获得初始化的$w_0$ ,再用logistic regressiow_0n模型进行最优化解。
Stochastic Gradient Descent
之前介绍的PLA算法和logistic regression算法,都是用到了迭代操作。PLA每次迭代 只会更新一个点,它每次迭代的时间复杂度是O(1);而logistic regression每次迭代要对所有N个点都进行计算,它的每时间复杂度是O(N)。为了提高logistic regression中 gradient descent算法的速度,可以使用另一种算法:随机梯度下降算法(Stochastic Gradient Descent)。
随机梯度下降算法每次迭代只找到一个点,计算该点的梯度,作为我们下一步更新w的依据。这样就保证了每次迭代的计算量大大减小,我们可以把整体的梯度看成这个随机过程的一个期望值。

随机梯度下降可以看成是真实的梯度加上均值为零的随机噪声方向。单次迭代看,好 像会对每一步找到正确梯度方向有影响,但是整体期望值上看,与真实梯度的方向没 有差太多,同样能找到最小值位置。随机梯度下降的优点是减少计算量,提高运算速 度,而且便于online学习;缺点是不够稳定,每次迭代并不能保证按照正确的方向前 进,而且达到最小值需要迭代的次数比梯度下降算法一般要多。

对于logistic regression的SGD,它的表达式为:
\[w_{t+1} \leftarrow w_t + \eta \theta (-y_n w_t^T x_n)(y_nx_n)\]我们发现,SGD与PLA的迭代公式有类似的地方,如下图所示:
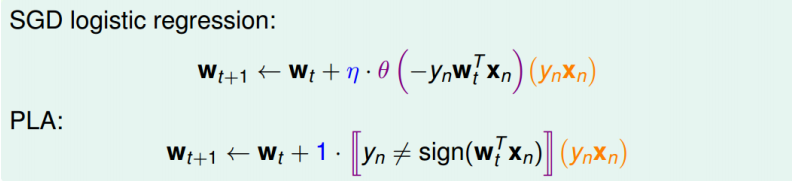
我们把SGD logistic regression称之为’soft’ PLA,因为PLA只对分类错误的点进行修正,而SGD logistic regression每次迭代都会进行或多或少的修正。另外,当$\eta = 1$, 且$w_t^T x_n$足够大的时候,PLA近似等于SGD。

除此之外,还有两点需要说明:1、SGD的终止迭代条件。没有统一的终止条件,一 般让迭代次数足够多;2、学习速率 。 的取值是根据实际情况来定的,一般取值0.1 就可以了。
Multiclass via Logistic Regression
假设平面上有四个类,分别是正方形、菱形、三角形和星形, 如何进行分类模型的训练呢?
首先我们可以想到这样一个办法,就是先把正方形作为正类,其他三种形状都是负类,即把它当成一个二分类问题,通过linear classification模型进行训练,得出平面上 某个图形是不是正方形,且只有{-1,+1}两种情况。然后再分别以菱形、三角形、星形 为正类,进行二元分类。这样进行四次二分类之后,就完成了这个多分类问题。
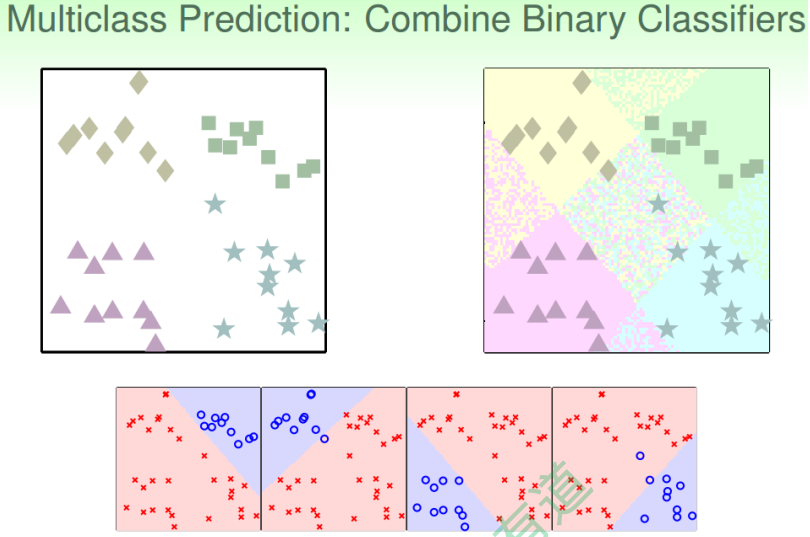
但是,这样的二分类会带来一些问题,因为我们只用{-1,+1}两个值来标记,那么平面上某些可能某些区域都被上述四次二分类模型判断为负类,即不属于四类中的任何 一类;也可能会出现某些区域同时被两个类甚至多个类同时判断为正类,比如某个区 域又判定为正方形又判定为菱形。那么对于这种情况,我们就无法进行多类别的准确判断,所以对于多类别,简单的binary classification不能解决问题。
针对这种问题,我们可以使用另外一种方法来解决:soft软性分类,即不用{-1,+1}这 种binary classification,而是使用logistic regression,计算某点属于某类的概率、可能性,去概率最大的值为那一类就好。
soft classification的处理过程和之前类似,同样是分别令某类为正,其他三类为负,不同的是得到的是概率值,而不是{-1,+1}。最后得到某点分别属于四类的概率,取最 大概率对应的哪一个类别就好。效果如下图所示:
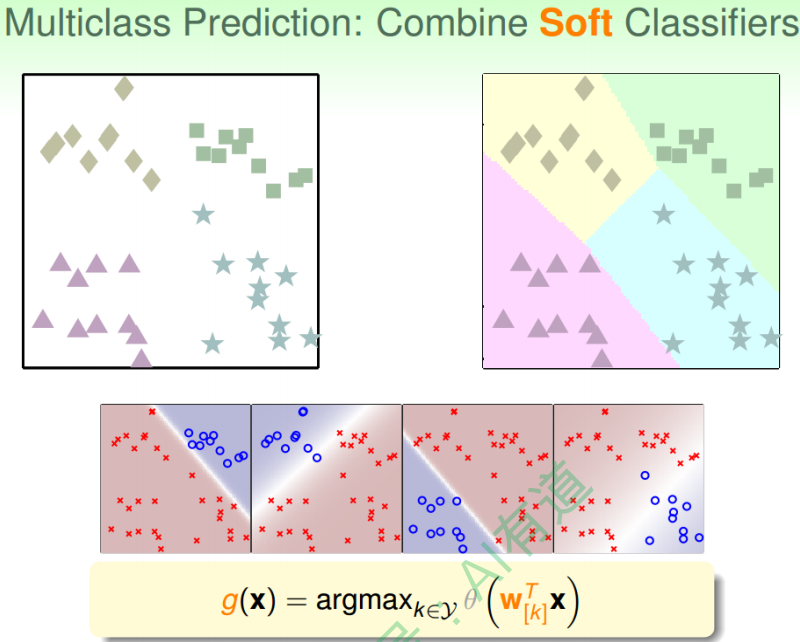
这种多分类的处理方式,我们称之为One-Versus-All(OVA) Decomposition。这种方法 的优点是简单高效,可以使用logistic regression模型来解决;缺点是如果数据类别很 多时,那么每次二分类问题中,正类和负类的数量差别就很大,数据不平衡 unbalanced,这样会影响分类效果。

Multiclass via Binary Classification
多分类算法OVA,这种方法存在一个问题,就是当类别k很多的时候,造成正负类数据unbalanced,会影响分类效果,表现不好。现在,我们介绍 另一种方法来解决当k很大时,OVA带来的问题。
这种方法呢,每次只取两类进行binary classification,取值为{-1,+1}。假如k=4,那 么总共需要进行$C_4^2 = 6$ 次binary classification。那么,六次分类之后,如果平面有个 ,有三个分类器判断它是正方形,一个分类器判断是菱形,另外两个判断是三角 形,那么取最多的那个,即判断它属于正方形,我们的分类就完成了。这种形式就如 同k个足球对进行单循环的比赛,每场比赛都有一个队赢,一个队输,赢了得1分,输 了得0分。那么总共进行了$C_k^2$次的比赛,最终取得分最高的那个队就可以了。
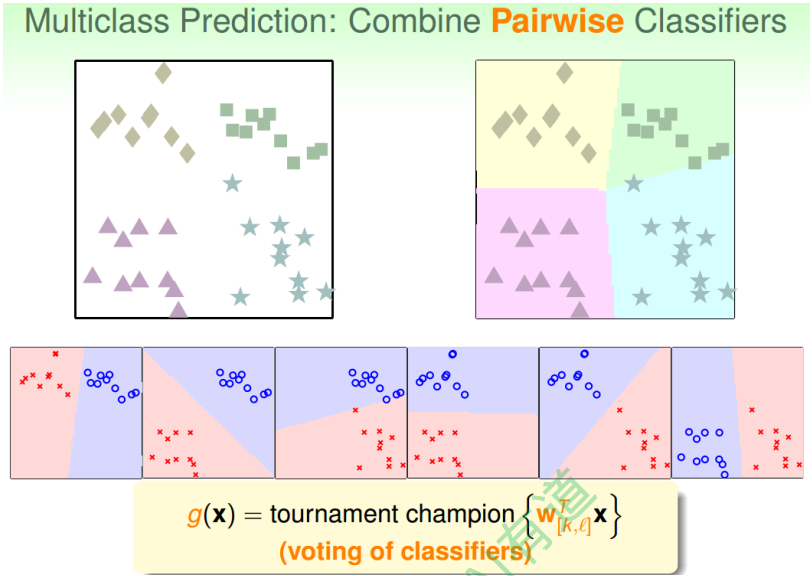
这种区别于OVA的多分类方法叫做OneVersusOne(OVO)。这种方法的优点是更加高 效,因为虽然需要进行的分类次数增加了,但是每次只需要进行两个类别的比较,也 就是说单次分类的数量减少了。而且一般不会出现数据unbalanced的情况。缺点是需 要分类的次数多,时间复杂度和空间复杂度可能都比较高。
