Logistic Regression Problem
一个心脏病预测的问题:根据患者的年龄、血压、体重等信息,来预测患者是否会有 心脏病。很明显这是一个二分类问题,其输出y只有{-1,1}两种情况。
二元分类,一般情况下,理想的目标函数f(x)>0.5,则判断为正类1;若f(x)<0.5,则判 断为负类-1。
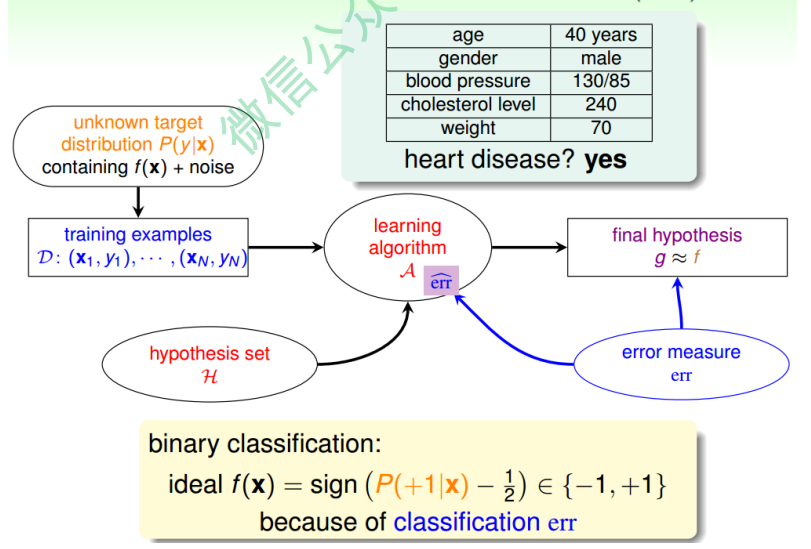
但是,如果我们想知道的不是患者有没有心脏病,而是到底患者有多大的几率是心脏病。这表示,我们更关心的是目标函数的值(分布在0,1之间),表示是正类的概率 (正类表示是心脏病)。这跟我们原来讨论的二分类问题不太一样,我们把这个问题 称为软性二分类问题(’soft’ binary classification)。这个值越接近1,表示正类的可能 性越大;越接近0,表示负类的可能性越大。
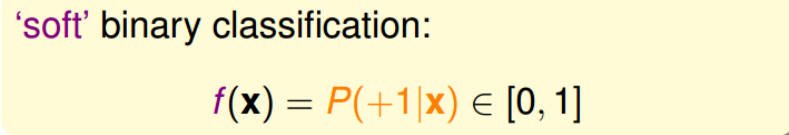
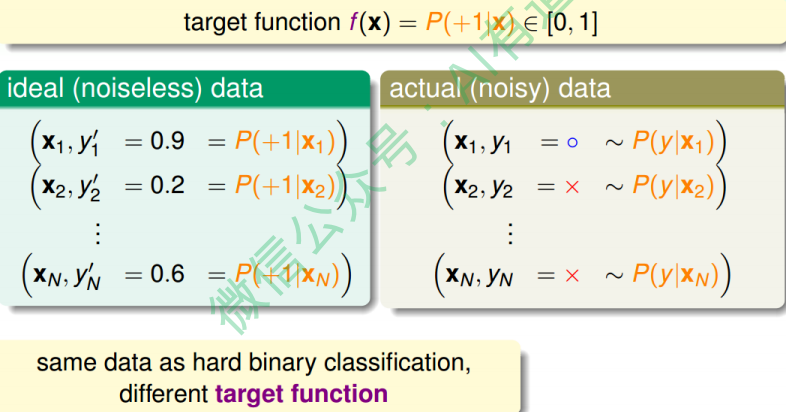
对于软性二分类问题,理想的数据是分布在[0,1]之间的具体值,但是实际中的数据只可能是0或者1,我们可以把实际中的数据看成是理想数据加上了噪声的影响。
如果目标函数是$f(x) = P(+1 \mid x) \in [0, 1]$的话,我们如何找到一个好的Hypothesis跟这个目标函数很接近呢?
首先,根据我们之前的做法,对所有的特征值进行加权处理。计算的结果s,我们称之 为’risk score’:

但是特征加权和$s \in (-\infty, +\infty)$,如何将s值限定在[0,1]之间呢?一个方法是使用 sigmoid Function,记为$\theta(s)$。那么我们的目标就是找到一个hypothesis:$h(x) = \theta(w^Tx)$。

Sigmoid Function函数记为$\theta(s) = \frac{1}{1 - e^{-s}}$, 满足$\theta(-\infty) = 0, \theta(0) = \frac{1}{2}, \theta(+\infty) = 1$。 这个函数是平滑的、单调的S型函数。 则对于逻辑回归问题, hypothesis就是这样的形式:
\[h(x) = \frac{1}{1 + e^{-w^Tx}}\]那我们的目标就是求出这个预测函数h(x),使它接近目标函数f(x)。
Logistic Regression Error
现在我们将Logistic Regression、Linear Classification、Linear Regression 做个比较:
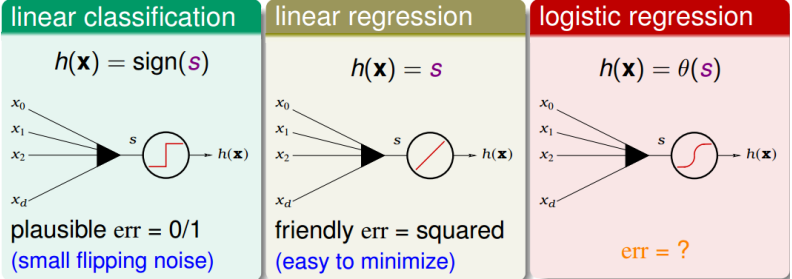
这三个线性模型都会用到线性scoring function $s = w^Tx$。linear classification的误差 使用的是0/1 err;linear regression的误差使用的是squared err。那么logistic regression的误差该如何定义呢?
先介绍一下“似然性”的概念。目标函数$f(x) = P(+1 \mid x)$,在所有的Hypothesis集合中找到一个 hypothesis与target function最接近,能产生同样的数据集D,包含y输出label,则称这 个hypothesis是最大似然likelihood。

logistic function: $h(x) = \theta(w^T x)$满足一个性质: $1 - h(x) = h(-x)$。那么,似然性h:
\[likelihood(h) = P(x_1)h(+x_1) \times P(x_2)h(-x_2) \times \cdots P(x_N)h(-x_N)\]因为$P(x_n)$对所有的h来说,都是一样的,所以我们可以忽略它。那么我们可以得到 logistic h正比于所有的$h(y_n x)$乘积。我们的目标就是让乘积值最大化。

如果将w代入的话:
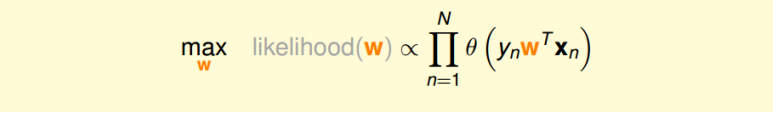
为了把连乘问题简化计算,我们可以引入ln操作,让连乘转化为连加:
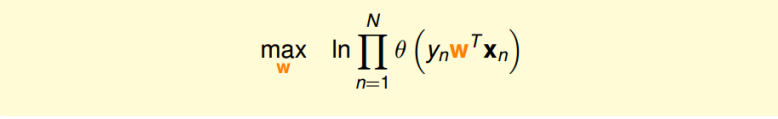
接着,我们将maximize问题转化为minimize问题,添加一个负号就行,并引入平均数操作$\frac{1}{N}$:
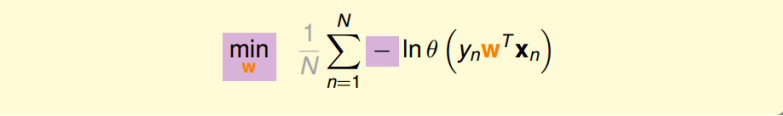
将logistic function的表达式带入,那么minimize问题就会转化为如下形式:
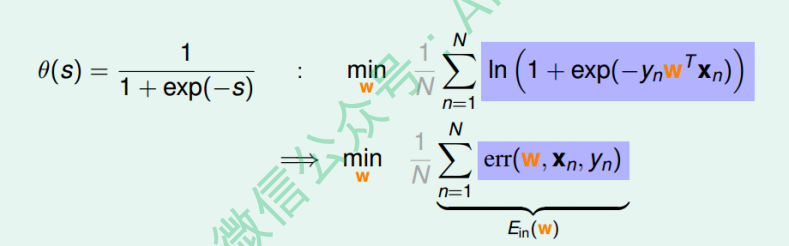
ps:这里的负号抵消掉了
至此,我们得到了logistic regression的err function,称之为crossentropy error交叉熵误差:

Gradient of Logistic Regression Error
我们已经推导了$E_{in}$的表达式,那接下来的问题就是如何找到合适的向量w,让$E_in$最小。
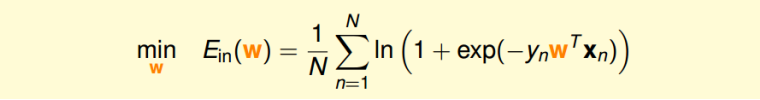
Logistic Regression的 是连续、可微、二次可微的凸曲线(开口向上),根据之前 Linear Regression的思路,我们只要计算$E_{in}$的梯度为零时的w,即为最优解。

对$E_{in}$计算梯度:
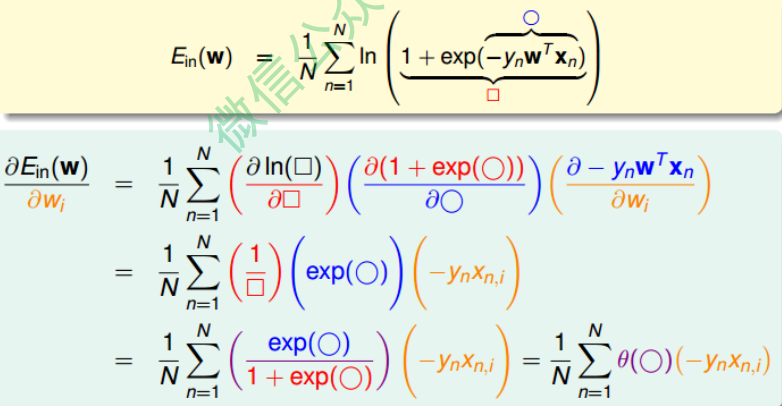
最终得到的梯度表达式为:
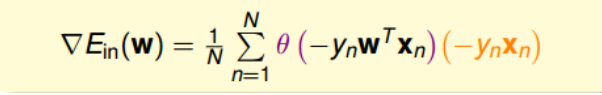
为了计算$E_{in}$最小值,我们就要找到让$\nabla E_{in}(w)$等于0的位置。
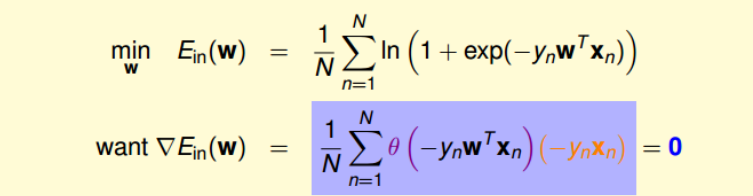
上式可以看成$\theta(-y_n w^T x_n)$是$-y_n x_n$的线性加权。要求$\theta(-y_n w^T x_n)$与$-y_nx_n$的 线性加权和为0,那么一种情况是线性可分,如果所有的权重$\theta(-y_n w^T x_n)$为0, 那么就能保证$\nabla E_{in}(w)$为0。$\theta(-y_nw^Tx_n)$是sigmoid function, 根据其特性, 只要让$-y_n w^T x_n « 0$, 即$y_n w^T x_n » 0$。 $y_n w^T x_n » 0$表示对于所有的点, $y_n$与$w^T x_n$都是同号的, 这表示数据集D必须是全部线性可分的才能成立。
回忆:什么叫线性可分?
回答:假设现在有一堆训练数据,它们是由两类点组成的,其中一类点用三角符号画在坐标系中,另一类点用圆圈画在坐标系中。现在拿出直尺和笔在坐标系中画一条直线,如果可以把三角点分到直线的一边,圆圈点分到直线的另一边的话,就说这个训练数据是线性可分的;否则,数据就是线性不可分的。
然而,保证所有的权重$\theta(-y_n w^T x_n)$为0是不太现实的,总有不等于0的时候,那么另一种常见的情况是非线性可分,只能通过使加权和为零,来求解w。这种情况没有 closed-form解,与Linear Regression不同,只能用迭代方法求解。

之前所说的Linear Regression有closed-form解,可以说是“一步登天”的;但是PLA算 法是一步一步修正迭代进行的,每次对错误点进行修正,不断更新w值。PLA的迭代 优化过程表示如下:

w每次更新包含两个内容:一个是每次更新的方向$y_n x_n$,用$v$表示,另一个是每次更新的步长$\eta$。参数$(v, \eta)$和终止条件决定了我们的迭代优化算法。

Gradient Descent
根据上一小节PLA的思想,迭代优化让每次w都有更新:
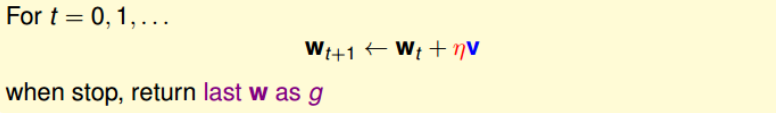
我们把$E_{in}(w)$曲线看做是一个山谷的话,要求$E_{in}(w)$最小,即可比作下山的过程。 整个下山过程由两个因素影响:一个是下山的单位方向$v$;另外一个是下山的步长$\eta$。

利用微分思想和线性近似,假设每次下山我们只前进一小步,即 很小,那么根据泰 勒Taylor一阶展开,可以得到:
\[E_{in}(w_t + \eta v) \approx E_{in}(w_t) + \eta v^T \nabla E_{in}(w_t)\]迭代的目的是让$E_{in}$越来越小,即让$E_{in}(w_t + \eta v) < E_{in}(w_t)$。 $\eta$是标量,因为如果两个向量方向相反的话,那么他们的内积最小(为负),也就是说如果方向$v$与梯度$\nabla E_{in}(w_t)$反向的话,那么就能保证每次迭代$E_{in}(w_t + \eta v) < E_{in}(w_t)$都成立。则,我们令下降方向$v$为:
\[v = -\frac{\nabla E_{in}(w_t)}{\|\nabla E_{in}(w_t)\|}\]$v$是单位向量, 每次都是沿着梯度的反方向走,这种方法称为梯度下降(gradient descent)算法。那么每次迭代公式就可以写成:
\[w_{t+1} \leftarrow w_t - \eta \frac{\nabla E_{in}(w_t)}{\| \nabla E_{in}(w_t) \|}\]思考:为什么是梯度方向的反方向走?
回答: 因为梯度方向是函数变化率最大的方向,因为要下降,所以往反方向走。
下面讨论一下$\eta$的大小对迭代优化的影响: $\eta$如果太小的话,那么下降的速度就会很慢; $\eta$如果太大的话,那么之前利用Taylor展开的方法就不准了,造成下降很不稳定, 甚至会上升。
因此, $\eta$应该选择合适的值,一种方法是在梯度较小的时候,选择小的$\eta$,梯度较大的时候,选择大的$\eta$,即$\eta$正比于$| \nabla E_{in}(w_t) |$。这样保证了能够快速、 稳定地得到最小值$E_{in}(w)$。
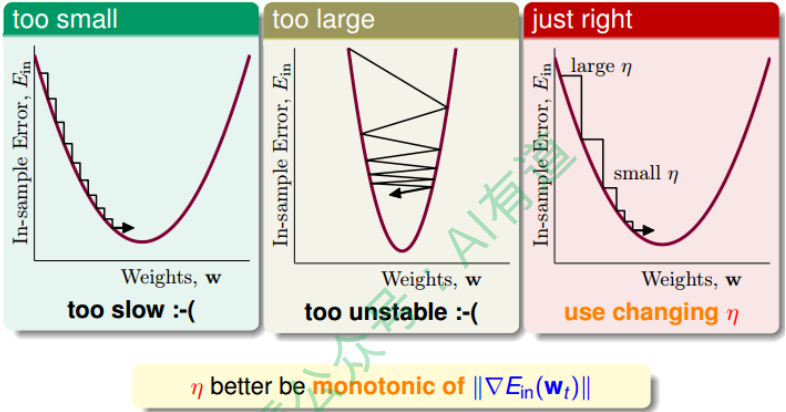
对学习速率 做个更修正,梯度下降算法的迭代公式可以写成:
\[w_{t+1} \leftarrow w_t - \eta' \nabla E_{in}(w_t)\]其中:
\[\eta' = \frac{\eta}{\| \nabla E_{in} (w_t)\|}\]总结一下基于梯度下降的Logistic Regression算法步骤如下:
- 初始化$w_0$
- 计算梯度$\nabla E_{in}(w_t) = \frac{1}{N} \sum_{n=1}^N \theta(-y_n w_t^T x_n)(-y_n x_n)$
- 迭代更新$w_{t+1} \leftarrow w_t - \eta \nabla E_{in}(w_t)$
- 满足$\nabla E_{in}(w_{t+1}) \approx 0$或者达到迭代次数, 迭代结束。