起步:用牛顿法解方程
原理分析
在解⼀元函数的⾼阶⽅程,形如$ax^n + bx^{n-1} + cx^{n-2} + \cdots + 1 = 0$时,⼤家肯定会想到⽤因式分解或者是⽤求根公式来获取⽅程的解析解,但是事实总不会是那么⼀帆⻛顺的,有时候复杂的 ⽅程我们没办法通过上述⽅法求取它的解,那么我们就得⽤迭代的⽅法来获取它的近似解,⽜顿法就是⼀种常⽤的⽅法。
它的理论基础还是基于函数的泰勒近似:
对于⽅程式$f(x)=0$,我们先选择⼀个点$x_0$作为⾸轮迭代的初始点,在$x_0$处对$f(x)$进⾏⼀阶泰勒展开:
\[f(x) \approx f(x_0) + (x - x_0)f'(x_0)\]⼤家知道,$f(x)$在$x = x_0$处的⼀阶泰勒展开$f(x_0) + (x - x_0)f’(x_0)$是函数$f(x)$在$x = x_0$处的切线,并以这条切线作为函数$f(x)$在$x = x_0$邻域的近似,那我们就通过这个直线⽅程$f(x_0) + (x - x_0)f’(x_0)$的根,来近似的作为$f(x)=0$的根。
具体获得的解如下:
\[f(x_0) + (x - x_0)f'(x_0) = 0 \Rightarrow x = x_0 - \frac{f(x_0)}{f'(x_0)}\]作为⼀条直线,获得这个切线⽅程的解是⼀件⾮常容易的事情,但是就这么求出来的解能够直接⽤来作为原⽅程$f(x)=0$的解吗?看看这误差,想想也不太敢直接⽤吧,下⾯这幅图显⽰得就⼀清⼆楚:
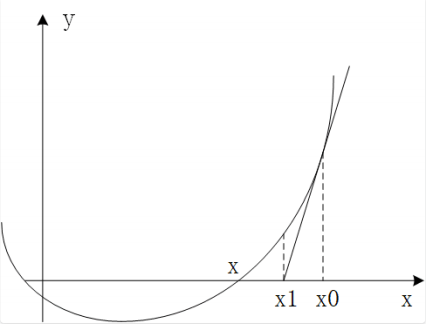
显然, 利用一阶泰勒展开式求得的近似解$x_1 = x_0 - \frac{f(x_0)}{f’(x_0)}$, 距离原⽅程$f(x)=0$真正的解距离还很远,但是它的的确确是⽐初始点$x_0$要更加接近于⽅程的真实解$x^*$,这也是⼀个好的趋势。
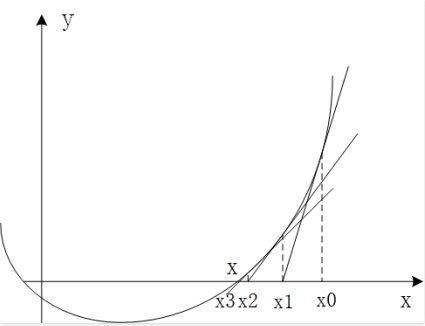
我们按照$x_{k+1} = x_k - \frac{f(x_k)}{f’(x_k)}$这个⽅法继续迭代下去,就会产⽣⼀个⽜顿法的近似解序列$x_1, x_2, x_3, …$,总的来说,它会越来越试图靠近⽅程的实际解析解,直到最后得到的两个相邻近似解之差小于预设的阈值$\epsilon$时(即此时满⾜$\mid x_{k+1} - x_k \mid < \epsilon$),这个迭代过程才停⽌,整个迭代的过程如下图所⽰: