从一元分布到多元分布
在⼀元⾼斯分布中,我们从⼀组样本$X = (x_1, x_2, x_3, …, x_N)$来引入, 我们基于这组样本中的$N$个样本值对⼀元⾼斯分布的两个参数进行极⼤似然估计。每⼀个样本都是⼀个随机变量,更直⽩的说就是⼀个随机的“数值”。
多元⾼斯分布中,同样我们也有⼀组这样的样本$X$,但是这⾥⾯的每⼀个样本 则不再是⼀个个的随机变量,而是多维的随机向量,每⼀个样本有p维:
\[x = \begin{bmatrix}x_1 \\ x_2 \\ x_3 \\ \cdots \\ x_p\end{bmatrix}\]我们假定有$N$个样本(随机变量),每⼀个样本有$p$维,那么可以集中将其对应的表⽰成矩阵的形式:
\[X = \begin{bmatrix} x_{11} & x_{12} & x_{13} & ... & x_{1p} \\ x_{21} & x_{22} & x_{23} & ... & x_{2p} \\ ... & ... & ... & ... & ... \\ x_{N1} & x_{N2} & x_{N3} & ... & x_{Np} \end{bmatrix}\]如何来解释这个$N$⾏$p$列的样本矩阵呢?
矩阵$X$有$N$⾏,代表了有$N$个样本,而$p$列代表了每⼀个样本有$p$个特征,或者说的直⽩些叫$p$个属性,就好⽐说这$N$个样本代表了某市的$N$个学⽣,而$p$个属性则分别可能是学⽣的⾝⾼、体重、考试成绩等等各种值。
而⼀元⾼斯分布则是$p = 1$的⼀种特殊情况,即每⼀个样本我们只看它的⼀个属性。此时的样本也可以看作是⼀个列为 1 的“特殊矩阵”了。
\[X = \begin{bmatrix} x_{11} \\ x_{21} \\ x_{31} \\ ... \\ x_{N1}\end{bmatrix}\]多元⾼斯分布的参数形式
和⼀元⾼斯分布类似,多元⾼斯分布的参数同样包含两个部分,⼀个⽤来描述分布的均值,另⼀个也是⽤来描述分布的⽅ 差,但是⼜有所不同:
⾸先⽤来描述分布均值的 不再是⼀个数值,而是⼀个和样本特征维度相对应的$p$维向量:
\[\mu = \begin{bmatrix}\mu_1 \\ \mu_2 \\ \mu_3 \\ ,,, \\ \mu_p\end{bmatrix}\]而向量$\mu$中的每⼀维$\mu_i$则具体反映了分布中第$i$个特征的均值。
而反映⽅差的参数也不再是⼀个数值,而是⼀个协⽅差矩阵 ,它是⼀个$p \times p$的矩阵:
\[\Sigma = \begin{bmatrix} \sigma_{11} & \sigma_{12} & \sigma_{13} & ,,, & \sigma_{1p} \\ \sigma_{21} & \sigma_{22} & \sigma_{23} & ... & \sigma_{2p} \\ \sigma_{31} & \sigma_{32} & \sigma_{33} & ... & \sigma_{3p} \\ ... & ... & ... & ... & ... \\ \sigma_{p1} & \sigma_{p2} & \sigma_{p3} & ... & \sigma_{pp} \end{bmatrix}\]我们需要来仔细理解⼀下这个多元随机变量协⽅差矩阵$\Sigma$的细节,⾸先这个⽅阵对⻆线的值$\sigma_{ii}$表⽰的是分布中第$i$个特征属性的⽅差,而⾮对⻆线上的值$\sigma_{ij}$则表⽰分布中第$i$个特征属性和第$j$个特征属性的协⽅差,依据协⽅差的定义,它反映的是多元⾼斯分布中,第$i$个特征属性和第$j$个特征属性的相关性。
那么⽐较特殊的情况就是,当协⽅差矩阵$\Sigma$是⼀个对⻆矩阵,即所有⾮对⻆位置上的值均为 0 的时候,意味着该分布中,不同特征属性之间都是不具备相关性的。
⼆元⾼斯分布的具体⽰例
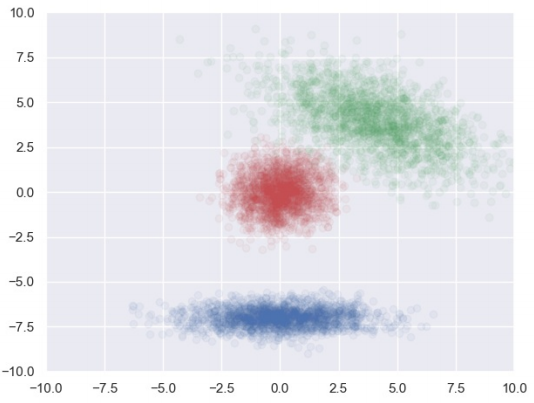
我们设置了三个不同参数的⼆元⾼斯分布,它们整体上的分布都呈现出椭圆形(或正圆形),但是我们发现由于均值向量$\mu$和协⽅差矩阵$\Sigma$设置的不同,三个分布呈现出不同的形态特点:
红色的分布1:
\[\mu = \begin{bmatrix}0 \\ 0\end{bmatrix}, \Sigma = \begin{bmatrix}1 & 0 \\ 0 & 1\end{bmatrix}\]分布中包含两维特征属性,均值均为 0,⽅差均为 1,协⽅差为 0,因此整个分布的中⼼点为 (0,0),两维特征属性彼此不相 关,因此分布形态为⼀个正圆。
蓝色的分布2:
\[\mu = \begin{bmatrix}0 \\ -7\end{bmatrix}, \Sigma = \begin{bmatrix}4 & 0 \\ 0 & 0.25\end{bmatrix}\]分布中包含的两维特征属性中,第⼆维特征属性的均值为 -7,因此整个分布的中⼼点位于 (0,-7),协⽅差矩阵同样是⼀个对⻆矩阵,因此两维特征彼此⽆关,因此椭圆的⻓短轴和 x 轴、y 轴⽅向⼀致,没有倾斜,但是不同的是,第⼀维特征属性的⽅差要明显⼤于第⼆维特征属性的⽅差,因此沿 x 轴⽅向的分布 要更加分散⼀些。
绿色的分布3:
\[\mu = \begin{bmatrix}4 \\ 4\end{bmatrix}, \Sigma = \begin{bmatrix}4 & -3 \\ -3 & 0.25\end{bmatrix}\]分布中唯⼀不同的就是协⽅差矩阵不再是⼀个对⻆矩阵,两维特征属性呈现出负相关,因此整个分布呈现出来的是⼀个左上 ⽅向的椭圆。
多元⾼斯分布的⼏何特征
从上⾯的例⼦中我们感性的认识到,⼆元⾼斯分布整体上是⼀个椭圆形,那我们如何从严格意义上来证明这⼀点呢?
我们假定$X$是⼀个$p$维的随机向量,服从$p$维⾼斯分布,它的两个参数为$p$维均值向量$\mu$和$p \times p$的协⽅差矩阵$\Sigma$ ,⾸先我们来看⼀下多元⾼斯分布的概率密度函数:
\[p(x \mid \theta) = \frac{1}{(2 \pi)^{\frac{p}{2}}\mid \Sigma \mid^{\frac{1}{2}}}e^{-\frac{1}{2}(x - \mu)^T \Sigma^{-1}(x - \mu)}\]对于一个特定的样本$x_i$, 它的概率密度值其实就取决于$-\frac{1}{2}(x - \mu)^T \Sigma^{-1} (x - \mu)$。
协⽅差矩阵是半正定的对称矩阵,可以得到由⼀组标准正交特征向量构成的特征矩阵。即, 矩阵$Q$可以表示成: $\begin{bmatrix}q_1 & q_2 & … & q_p\end{bmatrix}$。
协⽅差矩阵可以分解为$\Sigma = Q \Lambda Q^T$的形式,其中满⾜$QQ^T = I$,而$\Lambda=\begin{bmatrix}\lambda_1 &&& \ & \lambda_2 && \ &&…& \ &&& \lambda_p \end{bmatrix}$
因此协方差矩阵就可以写成:
\[\Sigma = \begin{bmatrix}q_1 & q_2 & ... & q_p \\ \end{bmatrix}\begin{bmatrix}\lambda_1 &&& \\ & \lambda_2 && \\ && ... & \\ &&& \lambda_p\end{bmatrix}\begin{bmatrix}q_1^T \\ q_2^T \\ ... \\ q_p^T\end{bmatrix} = \sum_{i=1}^p q_i \lambda_i q_i^T\] \[\Sigma^{-1} = (Q \Lambda Q^T)^{-1} = (Q^T)^{-1} \Lambda^{-1} Q^{-1} = Q \Lambda^{-1}Q^{-1}\]其中,对角矩阵
\[\Lambda^{-1} = \begin{bmatrix}\frac{1}{\lambda_1} &&& \\ & \frac{1}{\lambda_2} && \\ && ... & \\ &&& \frac{1}{\lambda_p}\end{bmatrix}\]因此:
\[\Sigma^{-1} = \sum_{i=1}^p q_i \frac{1}{\lambda_i}q_i^T\]我们回到上⾯那个决定概率密度的表达式: $(x - \mu)^T \Sigma^{-1}(x - \mu)$当中去。
\[(x - \mu)^T \Sigma^{-1}(x - \mu) = (x - \mu)^T [\sum_{i=1}^p q_i \frac{1}{\lambda_i}q_i^T](x - \mu) = \sum_{i=1}^P(x - \mu)^T q_i \frac{1}{\lambda_i}q_i^T(x - \mu)\]此时,我们对这个看似复杂的式⼦做⼀个小小变换和替代,令:
\[y_i = (x - \mu)^T q_i\]这是⼀个先平移、后投影的操作,先让随机变量$X$整体按照均值向量$\mu$进⾏平移,也就是使得原点称为分布的中⼼点,然 后向单位向量$q_i$做⼀个投影,这其中,很显然$y_1$是样本$x$在$q_1$⽅向上的投影⻓度,而$y_2$则是样本$x$在$q_2$⽅向上的投影⻓度,$q_1$和$q_2$是彼此正交的单位向量。
为了⽅便的说明问题,我们这⾥令维度$p=2$ ,那么等式就简化为:
\[\sum_{i=1}^2 (x - \mu)^T q_i \frac{1}{\lambda_i}q_i^T(x - \mu) = y_1 \frac{1}{\lambda_1} y_1^T + y_2 \frac{1}{\lambda_2}y_2^T = \frac{y_1^2}{\lambda_1} + \frac{y_2^2}{\lambda_2}\]那么, 最终的结论就是: 只要$\sum_{i=1}^2 (x - \mu)^T q_i \frac{1}{\lambda_i}q_i^T(x - \mu)$也就是$\frac{y_1^2}{\lambda_1} + \frac{y_2^2}{\lambda_2}$这个等式的值一固定, 那么整个二元高斯分布的概率密度函数
\[p(x \mid \theta) = \frac{1}{(2 \pi)^\frac{p}{2} \mid \Sigma \mid ^{\frac{1}{2}}}e^{- \frac{1}{2}(x - \mu)^T \Sigma^{-1}(x - \mu)}\]的值就确定了。
换句话说,就是 使得$\sum_{i=1}^2 (x - \mu)^T q_i \frac{1}{\lambda_i}q_i^T(x - \mu)$ 等于某个具体的常数$c$的所有样本$x$, 出现的概率是一样大的。
思考: 这里是什么意思?
那么进一步等价为$\frac{y_1^2}{\lambda_1} + \frac{y_2^2}{\lambda_2}$等于常数c的时候, 样本出现的概率都是一样的。
$\frac{y_1^2}{\lambda_1} + \frac{y_2^2}{\lambda_2} = c$的几何含义代表什么?
我们先令$c = 1$, 此时$\frac{y_1}{\lambda_1} + \frac{y_2}{\lambda_2} = 1$表示的就是一个椭圆的方程。
只不过这个椭圆的长轴和短轴发生了变化, 不再是我们印象中的$x$轴和$y$轴, 而是协方差矩阵经过特征值分解得到的两个标准正交的特征向量$q_1$和$q_2$, 他们构成了这个椭圆的长轴和短轴, 而这个椭圆在两个轴上的长度就是$\sqrt{\lambda_1}$和$\sqrt{\lambda_2}$, 而$y_1$和$y_2$就是原来$xoy$坐标系中的样本在$q_1$和$q_2$上的投影长度, 就是样本点以$q_1$和$q_2$为新坐标系的坐标值。
那么进⼀步我们来看,对于等式$\sum_{i=1}^2 (x - \mu)^T q_i \frac{1}{\lambda_i}(x - \mu)$, 每固定一个常数$c$, 就相当于在平面上以$q_1$和$q_2$为轴, $\sqrt{c \lambda_1}$和$\sqrt{c \lambda_2}$为轴长, 画了一个椭圆, 而这个椭圆上所有的样本点出现的概率是相等的。
随着常数c不断增大, 也就是$\sum_{i=1}^2 (x - \mu)^T q_i \frac{1}{\lambda_i}q_i^T(x - \mu)$的取值不断增大, 椭圆也在不断地增大, 而$p(x \mid \theta) = \frac{1}{(2 \pi)^{\frac{p}{2}}\mid \Sigma \mid ^{\frac{1}{2}}}e ^{-\frac{1}{2}(x - \mu)^T \Sigma^{-1}(x - \mu)}$的取值不断地减小, 越大的椭圆上分布的样本概率越小。
# ⼆元⾼斯分布⼏何特征实例分析
我们结合下⾯这个例⼦,把上⾯的分析过程总结⼀下,以下⾯这个⼆元⾼斯分布为例,分布的参数如下:
\[\mu = \begin{bmatrix}20 \\ -20\end{bmatrix}, \Sigma = \begin{bmatrix}34 & 12 \\ 12 & 41\end{bmatrix}\]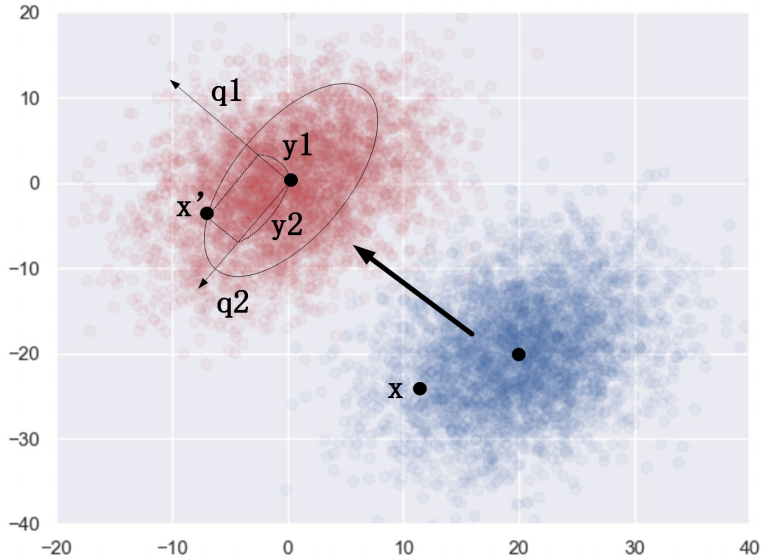
在图中,蓝⾊的为原始的⼆维⾼斯分布的样本点,样本减去均值向量$\mu = \begin{bmatrix}20 \ -20\end{bmatrix}$之后,整体平移⾄红⾊的分布区域。
我们对协方差矩阵$\Sigma = \begin{bmatrix}34 & 12 \ 12 & 41\end{bmatrix}$进⾏特征值分解得到特征向量$q_1 = \begin{bmatrix}-0.8 \ 0.6\end{bmatrix}$和$q_2 = \begin{bmatrix}-0.6 \ -0.8\end{bmatrix}$, 它们分别对应特征值为: $\lambda_1 = 25、\lambda_2 = 50$。
这意味着在平移后的红色区域中,拥有无数个以$\begin{bmatrix}0 \ 0\end{bmatrix}$为中心, 以$q_1$和$q_2$为轴的同心椭圆, 椭圆的长轴短轴之比$\frac{\sqrt{50}}{\sqrt{25}}$, 每个椭圆上的样本存在的概率相等,椭圆越⼤,样本存在的概率越小,这⾥我们从图中由⾥到外颜⾊由深变浅就能很 好地看出来。