高斯判别的前提假设回顾
和高斯判别分析⼀样,朴素贝叶斯分类器也是⼀种生成模型,并且也是针对联合概率进⾏建模:
\[y = argmax_{y \in 0, 1} p(y \mid x) = \text{argmax } p(x)p(x \mid y)\]并且都对先验概率$p(x \mid y)$有着非常强的假设前提,也正是因为这些很强的假设前提,才让我们的模型变得简化。
回忆先验、后验、似然函数的概念:
贝叶斯公式:
\(P(\theta \mid x) = \frac{p(x \mid \theta)p(\theta)}{p(x)}\)
$x$: 观察得到的数据(结果)
$\theta$:决定数据分布的参数(原因)
$p(\theta \mid x)$: posterior
$p(\theta)$: prior
$p(x \mid \theta)$: likelihood
$p(x)$: evidence
高斯判别分析中,它假设在指定类别$y = C_i$的情况下,概率$p(x \mid y = C_i)$满足高斯分布$p$,高斯分布的维度和样本特征的维度$p$一致, 不同类别的⾼斯分布仅仅只有均值不同,但是协⽅差矩阵都是⼀样的,如下图所⽰。
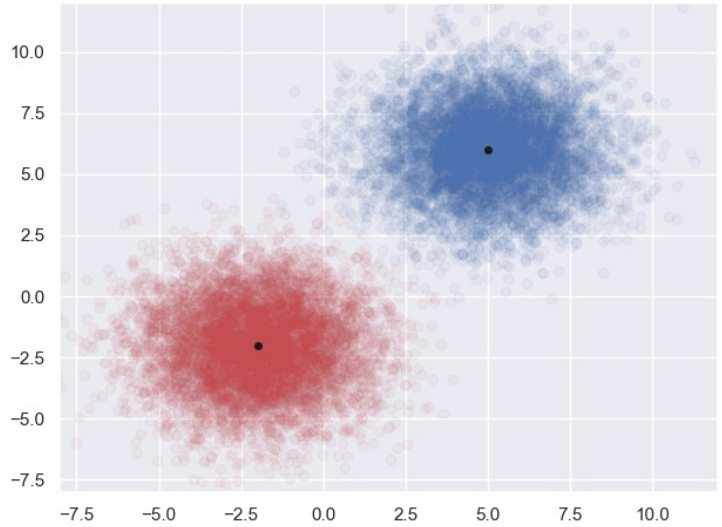
上图中我们可以看出,对于平⾯上任意⼀个点,它既可能属于$C_1$,也可能属于$C_2$,那么到底属于哪⼀类,就要看$p(y=C_1)p(x \mid y = C_1)$和$p(y = C_2)p(x \mid y = C_2)$谁更大。
朴素贝叶斯的前提假设
朴素⻉叶斯也有⼀个前提假设,同样我们也假设随机变量$y$表⽰分类, $y \in {0, 1}$, 而样本$x$是一个$p$维的随机向量, $x \in R^p$代表了样本的$p$个特征属性, 给定一个具体的样本$x$的时候, 如何判定它具体应该属于哪⼀个类别?
我们假定给定一组样本:
\[(x_i, y_i)_{i=1}^N\]其中$x_i \in R^p, y_i \in {0, 1}$, 这⾥也假定是⼀个⼆分类问题,当然多分类问题的道理也是⼀样,没有什么不同。
\[y = argmax_{y \in 0, 1} p(y \mid x) = \text{argmax }p(y)p(x \mid y)\]这⾥问题的关键仍然是$p(x \mid y)$,⾼斯判别分析⾥,我们假设给定$y$的分类取值的情况下, $x \mid y$服从⼀个$p$维的⾼斯分布,然 后就得到了$p(x \mid y)$的表达式, 使得我们可以获得似然函数的表达式。
朴素⻉叶斯分类器当中, 我们也有⼀个假设,那就是条件独立性假设,即在给定分类$y$的情况下,样本$x$的$p$个维度属性之间是独⽴的:
\[x_i \perp x_j \mid y\]有了条件独⽴的假设之后,我们就很容易地对$p(x \mid y)$进⾏处理了,即:
\[\begin{aligned} \text{argmax } p(y)p(x \mid y) & = \text{argmax}p(y)p(x_1, x_2, x_3, ..., x_p \mid y) \\ & = \text{argmax } p(y)p(x_1 \mid y)p(x_2 \mid y)p(x_3 \mid y) ... p(x_p \mid y) \end{aligned}\]以上,就是通过条件独⽴性进⾏的式⼦处理,那么后⾯再该怎么办?
我们⼀样需要求得最⼤的似然函数值,但是这⾥我们不需要像⾼斯判别分析中那样进⾏复杂的求导运算来对参数进⾏估计, 这⾥⽆论是$p(y)$还是$p(x_i \mid y)$都可以通过我们的样本集进⾏直接统计得到。
贝叶斯
| 序号 | 驾龄 | 平均车速 | 性别 |
|---|---|---|---|
| 1 | 1 | 60 | 男 |
| 2 | 2 | 80 | 男 |
| 3 | 3 | 80 | 男 |
| 4 | 2 | 80 | 男 |
| 5 | 1 | 40 | 男 |
| 6 | 2 | 40 | 女 |
| 7 | 1 | 40 | 女 |
| 8 | 1 | 40 | 女 |
| 9 | 3 | 60 | 女 |
| 10 | 3 | 80 | 女 |
此时,当我们拿到⼀个样本,此⼈驾龄 2 年,平均⻋速 80,我们来⽤朴素⻉叶斯分类器来推测此⼈的性别:
那么此时分类$y = {男, 女}$, 样本有两个特征, 其中$x_1$表示驾龄, $x_2$表示平均车速。
那么,我们来计算不同分类下的$p(y)p(x_1 \mid y)p(x_2 \mid y)$,来看哪个⼤。
\[p(y = 男)p(x_1 = 2 \mid y = 男)p(x_2 = 80 \mid y = 男) = 0.5 * 0.4 * 0.6 = 0.12\] \[p(y = 女)p(x_1 = 2 \mid y = 女)p(x_2 = 80 \mid y = 女) = 0.5 * 0.2 * 0.2 = 0.02\]因此我们选择使得似然函数取值最⼤的$y$值,显然,我们推测此⼈为男性。
条件独立性引申思考
实际上针对我们建模的联合概率分布 ,我们依据概率的链式法则进⾏展开:
\[\begin{aligned} p(y, x) & = p(y, x_1, x_2, x_3, ..., x_p) \\ & = p(x_1 \mid x_2, ..., x_n, y) ... p(x_{n-2} \mid x_{n-1}, x_n, y)p(x_{n - 1} \mid x_n, y)p(x_n \mid y)p(y) \end{aligned}\]而这⾥引⼊的条件独⽴性假设$x_i \perp x_j \mid y$ ,指的就是:
\[p(x_i \mid x_{i+1}, x_{i+2}, ..., x_n, y) = p(x_i \mid y)\]也就是在给定$y$的条件下, $x_i$以外的特征取值与否,都不影响$x_i$出现的条件概率,因此整个概率的链式等式得以最终化简。
实际上,这个前提假设其实是⾮常强的,因此在正常情况下,$x_i$和$x_j$⼀般都是有关联的,可能并不是相互独⽴的,但是特征属性之间的相关性⼜会在特征数量较多的时候,在⾼维的情况下带来极⼤的复杂性,因此⼀些出于简化模型的前提假设就提出来了,这⾥的条件独⽴性假设就是其中⼀种。
朴素⻉叶斯模型也是最简单的⼀种有向的概率图模型,它的概率图表⽰如下所⽰,当然概率图的内容我们后续会专题介绍, 这⾥不太清楚也没有关系,有个印象就好了。
随机过程中的⻢尔科夫性也同样属于这⼀类情况,例如⼀阶⻢尔科夫性定义为,下⼀时刻的状态只与当前状态有关,与过去 的状态⽆关:

同样地,这种马尔科夫性的前提假设⼀样地也能在概率的链式法则中帮助我们进⾏化简,这⾥就不展开了,后⾯随机过程和概率图模型中还会花大篇幅去讲。
