高斯过程概述
从字面上分解,我们就可以看出它包含两部分:
- 高斯,指的是高斯分布
- 过程,指的是随机过程
⾸先当随机变量是 1 维的时候,我们称之为⼀维高斯分布,概率密度函数$p(x) = N(\mu, \sigma^2)$,当随机变量的维度上升到有限的$p$维的时候,就称之为⾼维⾼斯分布,$p(x) = N(\mu, \Sigma_{p \times p})$ 。而高斯过程则更进⼀步,它是⼀个定义在连续域上的⽆限多个 ⾼斯随机变量所组成的随机过程,换句话说,⾼斯过程是⼀个⽆限维的高斯分布。
我们用符号来更严谨地描述:
对于⼀个连续域$T$(假设它是⼀个时间轴),如果我们在连续域上任选$n$个时刻: $t_1, t_2, t_3, …, t_n \in T$,使得获得的⼀个$n$维向量$\xi_1, \xi_2, \xi_3, .., \xi_n$都满足其是⼀个$n$维⾼斯分布,那么这个$\xi_t$就是⼀个高斯过程。
高斯过程的一个实际例子
在下面的图中, 横轴$T$是一个关于时间的连续域, 表示人的一生, 而纵轴表示的是体能值, 对于同一个人种的男性而言, 在任意不同的时间点体能值都服从正态分布, 但是不同时间点分布的均值和方差不同。
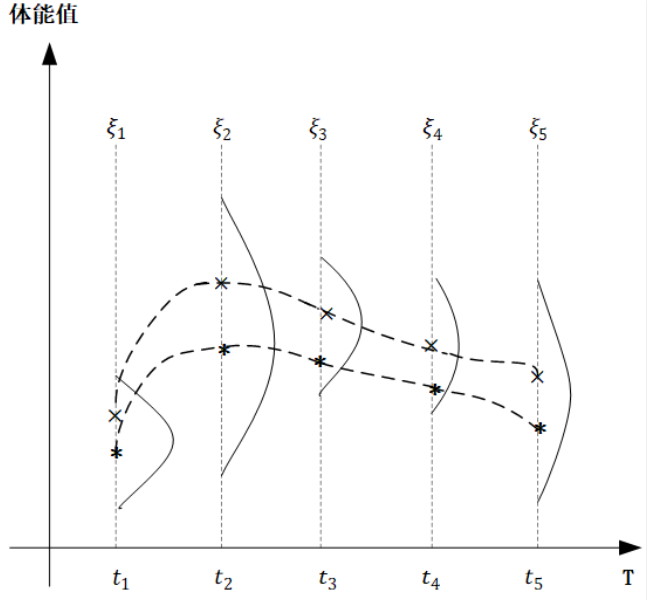
图中,我们取出了$t_1, t_2, t_3, t_4, t_5$五个时间点, 分别代表同一个男性群体童年、少年、青年、中年、老年的具体时刻, $\xi_1, \xi_2, \xi_3, \xi_4, \xi_5$分别对应五个时刻的体能值, 它们都服从高斯分布, 从图中可以看出, 均值和方差都不同。
对于任意$t \in 连续时间轴T$, $\xi_t \thicksim N(\mu_t, \sigma^2_t)$,也就是对于⼀个确定的高斯过程而⾔,对于任意时刻$t$,它的$\mu_t$和$\sigma_t^2$都已经确定了。而像上图中,我们对同⼀⼈种男性体能值在关键节点进⾏采样,然后平滑连接,也就是图中的两条虚线,就形成了 这个高斯过程中的两个样本。
高斯过程的核心要素和严谨描述
我们把高斯过程看作无限维的高斯分布。
对于一个$p$维的高斯分布而言, 决定它的分布是两个参数, 一个是$p$维的均值向量$\mu_p$, 它反映了$p$w维高斯分布中,每一维随机变量的期望, 另一个就是$p \times p$的协方差矩阵$\Sigma_{p \times p}$, 它反映了高维分布中,每一维自身的方差,以及不同维度之间的协方差。
定义在连续域$T$上的高斯过程其实也是⼀样,它是无限维的高斯分布,它同样需要描述每⼀个时间点$t$上的均值,但是这个时候就不能用向量了,因为是在连续域上的,维数是无限的,因此就应该定义成⼀个关于时刻$t$的函数:$m(t)$ 。
协⽅差矩阵也是同理,⽆限维的情况下就定义为⼀个核函数$k(s, t)$,其中$s$和$t$表⽰任意两个时刻。 核函数也称协⽅差函数。核函数是⼀个⾼斯过程的核⼼,它决定了⾼斯过程的性质,在研究和实践中, 核函数有很多种不同的类型,它们对⾼斯过程的衡量⽅法也不尽相同,这⾥我们介绍和使⽤最为常⻅的⼀个核函数:径向基函数$RBF$, 其定义如下:
\[k(s, t) = \sigma^2 e^{-\frac{\|s - t\|^2}{2 l^2}}\]核函数类比于协方差
\[\begin{aligned} Cov(X, Y) & = E[(X - E[X])(Y - E[Y])] \\ & = E[XY] - 2E[Y]E[X] + E[X]E[Y] \\ & = E[XY] - E[X]E[Y] \end{aligned}\]这里面的$\sigma$和$l$是径向基函数的超参数, 是我们提前可以设置好的, 例如我们可以让$\sigma = 1, l=1$, 从这个式子中,我们可以解读出它的思想:
$s$和$t$表示高斯过程连续域上的两个不同的时间点, $|s - t|^2$是一个二范式, 简单点说就是$s$和$t$之间的距离,径向基函数输出的是⼀个标量,它代表的就是$s$和$t$两个时间点各⾃所代表的⾼斯分布之间的协⽅差值,很明 显径向基函数是⼀个关于$s、 t$距离负相关的函数,两个点距离越⼤,两个分布之间的协⽅差值越小,即相关性越小,反之越靠近的两个时间点对应的 分布其协⽅差值就越⼤。
由此,⾼斯过程的两个核⼼要素——均值函数和核函数的定义我们就描述清楚了,按照⾼斯过程存在性定理,一旦这两个要素确定了,那么整个⾼斯过程就确定了:
\[\xi_t \thicksim GP(m(t), k(t, s))\]径向基函数的代码演示
1
2
3
4
5
6
7
8
9
10
11
12
13
import numpy as np
def guassian_kernel(x1, x2, l=1.0, sigma_f=1.0):
m, n = x1.shape[0], x2.shape[0]
dist_matrix = np.zeros((m, n), dtype=float)
for i in range(m):
for j in range(n):
dist_matrix[i][j] = np.sum((x1[i] - x2[j]) ** 2)
return sigma_f ** 2 * np.exp(-0.5 / l ** 2 * dist_matrix)
train_X = np.array([1, 3, 7, 9]).reshape(-1, 1)
print(guassian_kernel(train_X, train_X))
运行结果:
1
2
3
4
[[1.00000000e+00 1.35335283e-01 1.52299797e-08 1.26641655e-14]
[1.35335283e-01 1.00000000e+00 3.35462628e-04 1.52299797e-08]
[1.52299797e-08 3.35462628e-04 1.00000000e+00 1.35335283e-01]
[1.26641655e-14 1.52299797e-08 1.35335283e-01 1.00000000e+00]]
在这个函数中, 我们输入4个时间点: $t_1, t_2, t_3, t_4$, 输出的是一个$4 \times 4$的协方差矩阵, 反映的任意$t_i$和$t_j$两个时间点对应的高斯分布的协方差值, 当$i=j$时, 就是自身的协方差。
高斯过程回归原理详解
最后我们来看⾼斯过程回归。
这个过程我们其实可以看作是⼀个先验+观测值,然后推出后验的过程。
我们先通过$\mu(t)$和$k(s, t)$定义⼀个⾼斯过程,但是因为此时并没有任何的观测值,所以这是⼀个先验。
那么,如果我们获得了⼀组观测值之后,如何来修正这个⾼斯过程的均值函数和核函数,使之得到它的后验过程呢?
我们先回顾⼀下⾼维⾼斯分布的条件概率,我们知道,⾼斯分布有⼀个很好的特性,那就是⾼斯分布的联合概率、边缘概 率、条件概率仍然是满⾜⾼斯分布的,假设$n$维的随机变量满⾜⾼斯分布:
\[x \thicksim N(\mu, \Sigma_{n \times n})\]那么如果我们把这个$n$维的随机变量分成两部分, $p$维的$x_a$和q维的$x_b$, 满足$n = q + p$, 那么按照均值向量$\mu$和协方差矩阵$\Sigma$的分块规则, 就可以写成:
\[x = \begin{bmatrix}x_a \\ x_b\end{bmatrix}_{p+q} \quad \mu = \begin{bmatrix}\mu_a \\ \mu_b\end{bmatrix}_{p+q} \quad \Sigma = \begin{bmatrix}\Sigma_{aa} & \Sigma_{ab} \\ \Sigma_{ba} & \Sigma_{bb}\end{bmatrix}\]根据高斯分布的性质,我们知道下列条件分布依然是一个高维的高斯分布:
\[x_b \mid x_a \thicksim N(\mu_{b \mid a}, \Sigma_{b \mid a})\] \[\mu_{b \mid a} = \Sigma_{ba} \Sigma_{aa}^{-1} (x_a - \mu_a) + \mu_b\] \[\Sigma_{b \mid a} = \Sigma_{bb} - \Sigma_{ba}\Sigma_{aa}^{-1}\Sigma_{ab}\]思考: 什么性质?
高斯分布的性质:
设$X \thicksim N(\mu, \sigma^2)$, 其分布函数为$F(x)$, 则
- $f(x) = \Phi(\frac{x - \mu}{\sigma})$, $\frac{X - \mu}{\sigma} \thicksim N(0, 1)$
- 当$x_1 < x_2$时, $P{x_1 < X \leq x_2} = \Phi(\frac{x_2 - \mu}{\sigma}) - \Phi(\frac{x_1 - \mu}{\sigma})$
- 概率密度$f(x)$关于$x = \mu$对称, $\varphi(x)$是偶函数
- $\Phi(-x) = 1 - \Phi(x)$, $\Phi(0) = \frac{1}{2}$
- 当$X \thicksim N(0, 1)$时, $P{\mid X \mid \leq a} = 2 \Phi(a) - 1$, $a > 0$
二维高斯分布的性质, 设$(X, Y) \thicksim N(\mu_1, \mu_2; \sigma_1^2, \sigma_2^2; \rho)$,则:
- $X \thicksim N(\mu_1, \sigma_1^2)$, $Y \thicksim N(\mu_2, \sigma_2^2)$
- $X$与$Y$相互独立的充分必要条件时$\rho = 0$ 。 ($(X, Y)$ 服从二维正态分布可以保证$X$和$Y$均服从一维正态分布, 反过来则不能成立, 即已知$X$与$Y$均服从正态分布, 并不能保证$(X, Y)$服从二维正态分布。)
- $aX + bY \thicksim N(a\mu_1 + b\mu_2, a^2\sigma_1^2 + 2ab\sigma_1\sigma_2\rho + b^2\sigma_2^2)$
在数理统计中,常有随机变量$X_1, X_2, …, X_n$相互独立, 且$X_i \thicksim N(\mu, \sigma^2)$($i=1, 2, …, n$), 则有$\sum_{i=1}^n c_i X_i \thicksim N(\sum_{i=1}^n c_i \mu, \sum_{j=1}^n c_j^2 \sigma^2)$。
如果$X_1, X_2, …, X_n$相互独立且$X_i \thicksim N(\mu_i, \sigma_i^2)(i=1, 2, …, n)$, 则有: \(\sum_{i=1}^n c_i X_i \thicksim N(\sum_{i=1}^n c_i \mu_i, \sum_{j=1}^n c_j^2 \sigma_j^2)\)
也就是说,设置了高斯过程的先验参数, 一旦我们拿到一些观测值, 那么就可以对高斯过程的均值函数和核函数进行修正, 得到一个修正后的后验高斯过程,而更新后验参数的信息就来自于观测值。
那么将高斯过程对比高维高斯分布,我们把均值向量替换成均值函数, 把协方差矩阵替换成核函数, 就能够得到高斯过程基于观测值的后验过程的参数表达式。
我们的一组观测值, 它们的时刻对应一个向量$X$, 那么对应的值是另一个同维度的向量$Y$, 假设有4对观测值, 那就是:
\[(X[1], Y[1]), (X[2], Y[2]), (X[3], Y[3]), (X[4], Y[4])\]那么余下的所有非观测点,在连续域上我们定义为$X^$, 值定义为$f(X^)$。
首先, 联合分布显然是满足无限维高斯分布的:
\[\begin{bmatrix}Y \\ f(X^*)\end{bmatrix} \thicksim N(\begin{bmatrix}\mu(X) \\ \mu(X^*)\end{bmatrix}, \begin{bmatrix}k(X, X) & k(X, X^*) \\ k(X^*, X) & k(X^*, X^*)\end{bmatrix})\]从这个联合分布所派生出来的条件概率$f(X^) \mid Y$同样也服从高斯分布, 当然这里指的是无限维高斯分布, 对比一下, 把$Y$看作是$x_a$, 把$f(X^)$看作是$x_b$, 直接类比条件分布的参数表达式:
\[f(X^*) \mid Y \thicksim N(\mu^*, k^*)\]这里面的$\mu^$和$k^$就是条件分布下的后验高斯过程的均值函数和核函数的形式。
类比我们就可以写成表达式:
\[\mu^* = k(X^*, X)k(X, X)^{-1}(Y - \mu(X)) + \mu(X^*)\] \[k^* = k(X^*, X^*) - k(X^*, X)k(X, X)^{-1}k(X, X^*)\]高斯过程回归代码演示
在我们的例子中,高斯过程先验, 我们设置均值函数为$\mu(X) = 0$, 径向基函数$k(X, X^) = \sigma^2 e^{- \frac{|X - X^|^2}{2l^2}}$中的超参数为$l=0.5, \sigma = 0.2$。
然后我们$X = \begin{bmatrix}1, 3, 7, 9\end{bmatrix}$的位置上设置一组观测值, $Y$为$X$取正弦的基础上加上一点高斯噪声(这个$Y$的公式没有任何实际物理意义, 纯为随机选取):
\[y = 0.4sin(x) + N(0, 0.05)\]我们在四个观测点的基础上,来求高斯过程的后验。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
import matplotlib.pyplot as plt
import numpy as np
def gaussian_kernel(x1, x2, l=0.5, sigma_f=0.2):
m, n = x1.shape[0], x2.shape[0]
dist_matrix = np.zeros((m, n), dtype=float)
for i in range(m):
for j in range(n):
dist_matrix[i][j] = np.sum((x1[i] - x2[j]) ** 2)
return sigma_f ** 2 * np.exp(-0.5 / l ** 2 * dist_matrix)
def getY(X):
X = np.asarray(X)
Y = np.sin(X) * 0.4 + np.random.normal(0, 0.05, size=X.shape)
return Y.tolist()
def update(X, X_star):
X = np.asarray(X)
X_star = np.asarray(X_star)
K_YY = gaussian_kernel(X, X)
K_ff = gaussian_kernel(X_star, X_star)
K_Yf = gaussian_kernel(X, X_star)
K_fY = K_Yf.T
K_YY_inv = np.linalg.inv(K_YY + 1e-8 * np.eye(len(X)))
mu_star = K_fY.dot(K_YY_inv).dot(Y)
cov_star = K_ff - K_fY.dot(K_YY_inv).dot(K_Yf)
return mu_star, cov_star
f, ax = plt.subplots(2, 1, sharex=True, sharey=True)
X_pre = np.arange(0, 10, 0.1)
mu_pre = np.array([0] * len(X_pre))
Y_pre = mu_pre
cov_pre = gaussian_kernel(X_pre, X_pre)
uncertainty = 1.96 * np.sqrt(np.diag(cov_pre))
ax[0].fill_between(X_pre, Y_pre + uncertainty, Y_pre - uncertainty, alpha=0.1)
ax[0].plot(X_pre, Y_pre, label="expection")
ax[0].legend()
X = np.array([1, 3, 7, 9]).reshape(-1, 1)
Y = getY(X)
X_star = np.arange(0, 10, 0.1).reshape(-1, 1)
mu_star, cov_star = update(X, X_star)
Y_star = mu_star.ravel()
uncertainty = 1.96 * np.sqrt(np.diag(cov_star))
ax[1].fill_between(X_star.ravel(), Y_star + uncertainty, Y_star - uncertainty, alpha=0.1)
ax[1].plot(X_star, Y_star, label="expection")
ax[1].scatter(X, Y, label="observation point", c="red", marker="x")
ax[1].legend()
plt.show()
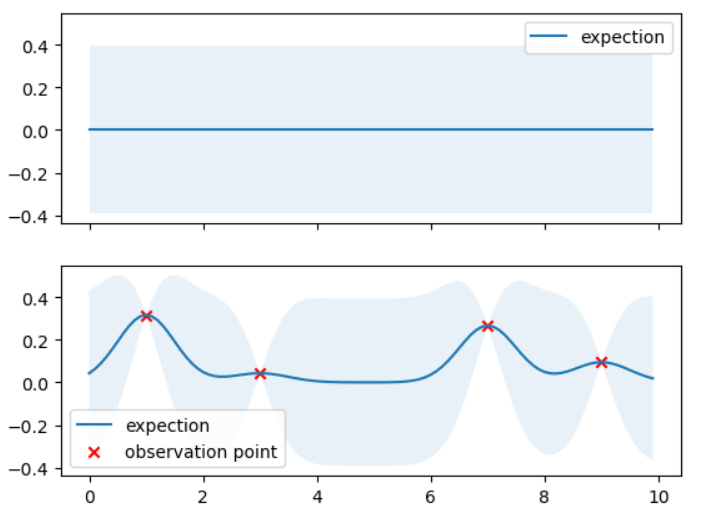
我们分析⼀下试验结果,图中浅蓝半透明区域表⽰在该点均值附近取 95% 置信区间的区域,上⾯⼀幅图是⾼斯过程的先验,下⾯是在四对观测值的基础上的⾼斯过程后验,明显可以看出,由于观测 点信息的带⼊,连续域上各个点的均值发⽣了变化,同时⼤部分取值点的 95% 置信空间也收窄了,证明确定性得到了增强。