马尔科夫链回顾
随机过程指的就是⼀个随机变量的序列$X_t$, 而马尔科夫链就是随机过程中的一种非常典型的类型,它的概率图如下:
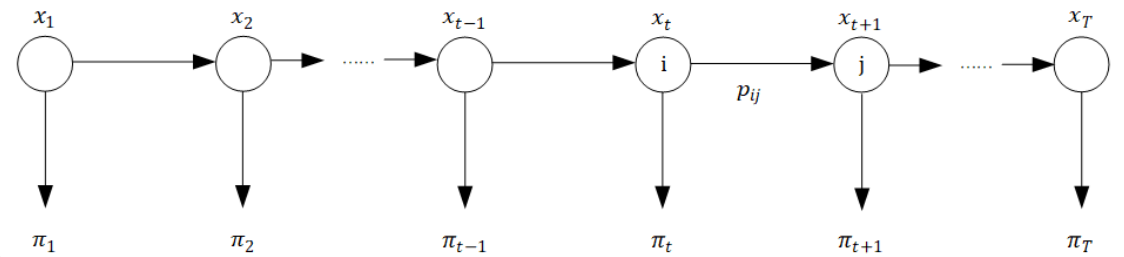
马尔科夫链在不同的时间$t$对应着不同的状态节点$x_t$, 实际上就是用时间串联起来的一个个随机变量, 这一组随机变量共享一个状态空间,其中包含$n$个状态, 每一个时间节点对应的随机变量都会取这个状态空间中的一个具体状态。
随着时间的不断向前移动, 马尔科夫链当中的不同状态节点就在不同的状态之间进行着转移, 这就派生了马尔科夫链中的另一个重要参数——状态转移矩阵$P$, 显然这个矩阵应该是一个$n \times n$的方阵:
\[P = \begin{bmatrix} p_{11} & p_{12} & p_{13} & ... & p_{1n} \\ p_{21} & p_{22} & p_{23} & ... & p_{2n} \\ p_{31} & p_{32} & p_{33} & ... & p_{3n} \\ ... & ... & ... & ... & ... \\ p_{n1} & p_{n2} & p_{n3} & ... & p_{nn} \end{bmatrix}\]其中某个具体的元素$P_{ij}$表示从状态$i$转移到状态$j$的概率。用条件概率描述就是$P_{ij} = p(x_{t+1} = j \mid x_t = i)$。
这里我们只考虑一阶齐次马尔科夫链, 简单点说, 就是未来的状态只取决于现在, 而与过去无关。 用条件概率描述就是:
\[p(x_{t+1} = x \mid x_1, x_2, ..., x_t) = p(x_{t+1} = x \mid x_t)\]马尔科夫链概率图中每个时间$t$时刻节点对应的$\pi_t$表示$t$时刻的概率分布。 因为节点之间的状态是依照概率进行转移的, 也就是说任意时刻$t$节点,对于$n$个状态中的任意一个状态, 他都有可能取到, 因此$\pi_t$是一个向量, 对应的是在$t$时刻, $n$个不同状态中每一个状态出现的概率:
\[\pi_t = [\pi_t(1), \pi_t(2), \pi_t(3), ..., \pi_t(n)]\]并且满足:
\[\sum_{i=1}^n \pi_t(i) = 1\]那么依照状态转移的定义, 将$t$时刻和$t+1$时刻的状态分布$\pi_t, \pi_{t+1}$, 以及状态转移概率矩阵$P$结合起来就有:
\[\pi_{t+1}(x^*) = \sum_x \pi_t(x)p(x^* \mid x)\]这是什么含义? : 如果初始状态定了, 根据状态转移概率,某一时间各个状态出现的概率是确定的, 就是$\pi$。
这其中,$x$和$x^*$是这个马尔科夫链状态空间中$n$个状态里任意两个状态。
总体合成状态转移矩阵和状态分布向量之间相乘的形式就是:$\pi_tP = \pi_{t+1}$。
核心:马尔科夫链的平稳分布
对于某一个具体的马尔科夫链而言, 每一个时刻$t$都有一个状态分布$\pi_t$, 但是如果对于任意不同的时刻$t$和$t+1$, 它们的分布保持不变, 都为$\pi$的话,那么状态分布$\pi$就是这个马尔科夫链的平稳分布, 按照定义它满足:
\[\pi(x^*) = \sum_x \pi(x)p(x^* \mid x)\]而此时,平稳分布$\pi$和状态转移矩阵$P$满足:$\pi P = \pi$。
换句话说, 也就是意味着, 当从某个时刻$t$开始, 它的各个状态服从平稳分布$\pi$的话, 那么后续的任意时刻, 状态的分布都为平稳分布$\pi$。
马尔科夫链稳态的价值和意义
那么这个稳态有什么意义呢?⽐如进⼊到⻢尔科夫链的稳态之后,每⼀个不同的时刻$t$都会对应状态集中的⼀个状态,当然它是随机的,但是由于进⼊了稳态,它们都服从同样⼀个分布,也就是该⻢尔科夫链的稳态分布$\pi$,那么依照⼤数定律,将进⼊平稳状态之后的每个$t$时刻的状态都作为⼀个样本,而形成⼀个样本集,那么这个样本集就可以作为这个平稳分布的近似。
这⾥有两个问题,实际在⼯程中,如何判断是否进⼊到平稳分布?进⼊平稳分布前的时间我们称之为是“燃烧期”,那么如 果让燃烧期取⼀个相对较⻓的时间,⼀般而⾔就可以保证⻢尔科夫链进⼊到稳态。
第⼆,进⼊到稳态之后,采样的时间节点越多,那么样本集就越能够作为平稳分布的近似。
那么后续的思路就很直接了,如果要通过采样的⽅式去求取⽬标分布$p(z)$,那我们就引⼊⻢尔科夫链的稳态分布,让我们的⽬标分布恰为某⼀个⻢尔科夫链的稳态分布,那么我们在该⻢尔科夫 链上进⾏⻓时间的状态转移,燃烧期之后我们收集到进⼊稳态后各个时刻点的样本,该样本集就可以作为⽬标分布的⼀个近似了。
稳态判定:细致平稳条件
那么如何达到上述目标? 如何判断一个分布$\pi$式一个给定马尔科夫链的平稳分布?
给定一个马尔科夫链的状态转移矩阵$P$, 以及一个分布$\pi$, 如果满足: \(\pi(x)p(x^* \mid x) = \pi(x^*)p(x \mid x^*)\) 其中, $x$和$x^*$是该马尔科夫链状态空间中任意两个给定状态, 那么分布$\pi$就是该马尔科夫链的平稳分布。
由于$\pi(x) p(x^* \mid x) = \pi(x^)p(x \mid x^)$, 那么对等式两侧同时关于状态$x$所有的可取值进行求和:
\[\sum_x \pi(x)p(x^* \mid x) = \sum_x \pi(x^*)p(x \mid x^*) = \pi(x^*)\sum_x p(x \mid x^*)\]显然, 当$x$取遍状态集中所有的状态时, 有:
\[\sum_x p(x \mid x^*) = 1\]因此:
\[\sum_x \pi(x)p(x^* \mid x) = \pi(x^*)\]这个就是平稳分布的定义, 因此我们证明了细致平稳条件。