动态图模型的共性特征
有向图模型,也就是⻉叶斯⽹络模型中的⼀组典型案例——隐⻢尔可夫模型、卡尔曼滤波器和粒⼦滤波,这三个有向图模型都有⼀个统⼀的名字——动态图模型,它们拥有如下的通⽤概率图表达形式:
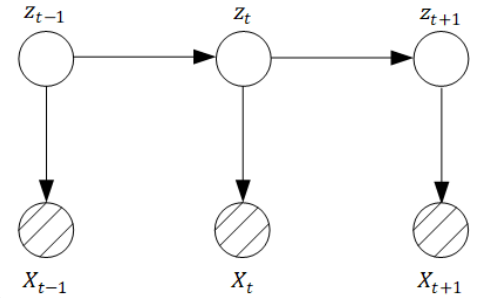
在上⾯的概率图中有⼏个很重要的要素:
- 第⼀个:在这个模型中,我们拥有观测变量 ,以及隐藏变量 ,代表了隐含状态;
- 第⼆个:就是可以看出这个模型中明显包含了⼀条时间轴。
隐⻢尔可夫模型、卡尔曼滤波器和粒⼦滤波这三种具体模型承袭于动态图模型,那么它们显然都具备动态图模型的 两个共同假设。
⼀个是基于隐变量序列 的,⻬次⻢尔科夫假设:即$Z_{t+1}$的取值只与$Z_t$有关,而与$Z_1, Z_2, …, Z_{t-1}$ 的各⾃取值均⽆关联。
\[p(Z_{t+1} \mid Z_t) = p(Z_{t+1} \mid Z_t, Z_{t-1}, Z_{t-2}, ..., Z_1)\]另一个是基于同一组观测变量$X_t$和隐含变量$Z_t$的关系, 即观测独立性假设: 观测变量$X_t$的取值只与隐含变量$Z_t$有关, 而与其他的观测变量、隐变量的取值均无关系。
\[p(X_t \mid Z_t) = p(X_t \mid Z_1, Z_2, ..., Z_T, X_1, ..., X_{t-1}, X_{t+1}, ..., X_T)\]几种模型各自的区别
这两个假设是这三个模型的共性特征,那么它们的区别在哪呢?就在于观测变量$X$和隐藏变量$Z$各⾃的变量分布形式,以及变量之间的关系上。
对于隐⻢尔可夫模型模型而⾔,要求隐变量必须是离散型随机变量,观测变量可以是离散的也可以是连续型的,相邻隐含变量$Z_t$和$Z_{t-1}$之间的转移过程以及隐含变量$Z_t$到观测变量$X_t$的输出过程都遵循状态转移矩阵中的概率约束。
对于卡尔曼滤波器而⾔,情况就有所不同,隐含变量$Z$和观测变量$X$都是连续型随机变量,并且都符合⾼斯分布。同时$Z_t$和$Z_{t-1}$间的关系以及隐含变量$Z_t$到观测变量 $X_t$的关系都是符合带有⾼斯噪声的线性关系。
而粒⼦滤波则具备更为⼀般性的情况,即隐含变量$Z$和观测变量$X$均不需要服从⾼斯分布,并且它们之间也不需要满⾜线性关系。
动态图模型的重点问题
- 第⼀类⼤问题我们称之为学习(learning):⽐如在隐⻢尔科夫模型中,我们会通过模型的观测值$X$,利⽤ EM ⽅法去迭代探索模型的参数:初始状态分布向量$\pi$,状态转移矩阵$A$和发射矩阵$B$。
- 第⼆类⼤问题我们称之为推断(inference):但它们本质上都是已知⼀组观测变量$X$,对我们所感兴趣的后验概率进⾏估计,但是推断的问题当中⼜分了很多具体的细类。
在隐⻢尔可夫模型中,我们⽐较关⼼状态解码:
状态解码(decoding)是已知⼀组观测变量$x_1, x_2, …, x_t$,去推断最可能对应的⼀组隐状态$z_1, z_2, …, z_t$,实际上就是去估计后验概率$p(z_1, z_2, …, z_t \mid x_1, x_2, …, x_t)$。
针对卡尔曼滤波或者粒子滤波主要有下面三类情形。
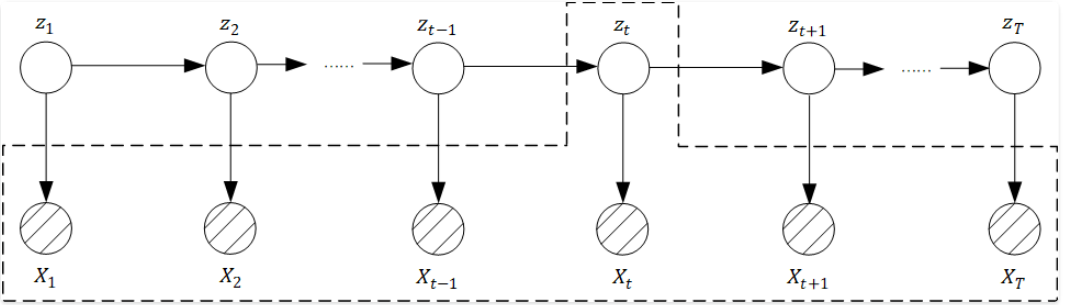
一种称之为滤波(filtering), 它需要去求的后验概率的形式为: $p(z_t \mid x_1, x_2, …, x_t)$。
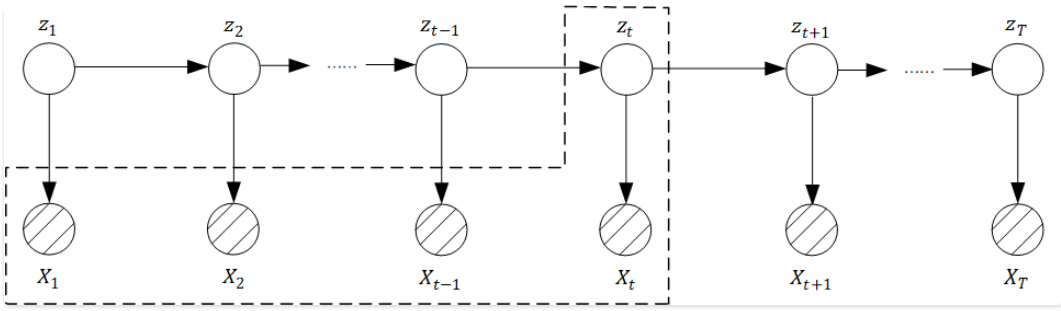
另一种就称之为平滑(smoothing), 它需要去求的后验概率的形式为: $p(z_t \mid x_1, x_2, x_3, …, x_T)$。
滤波和平滑的后验概率形式看上去挺像的, 但是有一点本质的区别, 滤波是起始的$t_1$开始, 当得到第$t$时间点的观测变量时, 对$t$时刻的隐含变量$Z_t$进行估计, 所以我们可以看出, 滤波的过程是随着时间的进行, 动态实时进行的, 因此滤波是一个在线过程,而平滑不同, 它是获得了所有$T$时间点的观测变量后, 对$t$时刻的隐含变量$Z_t$的概率进行估计。
第三类就是预测类问题(Predict),很显然顾名思义是通过直⾄当前时刻的观测变量,去预测下⼀时间点的状态变量$z_{t+1}$和观测变量$x_{t+1}$,即估计的是下⾯两类后验概率值:$p(z_{t+1} \mid x_1, x_2, …, x_t)$和$p(x_{t+1} \mid x_1, x_2, …, x_t)$。