问题
能够在$n$次多项式空间中另找一组基函数
\[\varphi_0(x), \varphi_1(x), ..., \varphi_n(x)\]使得:
\[P_n(x) = c_0 \varphi_0(x) + c_1\varphi_1(x) + ... + c_n \varphi_n(x)\]并且每增加一个插值节点时, 只需重新计算一个基函数。
牛顿插值法 就是基于这种想法提出来的。
牛顿插值法
牛顿插值函数:
\[N_n(x) = a_0 + a_1(x - x_0) + ... + a_n(x - x_0)(x - x_1) ... (x - x_n)\]基函数:
\[1, (x - x_0), (x - x_0)(x - x_1), ..., (x - x_0)(x - x_1)...(x - x_n)\]研究问题:
组合系数$a_0, a_1, a_2, …, a_n = ?$, 使得$N(x_i) = y_i(i = 0, 1, …, n)$。
\[N_n(x) = c_0 + c_1(x - x_0) + ... + c_n(x - x_0)(x - x_1)...(x - x_n)\]例如:
两点的线性插值多项式
\[\begin{aligned} P_1(x) & = y_0 + \frac{y_1 - y_0}{x_1 - x_0}(x - x_0) \triangleq N_1(x) \\ & \Rightarrow a_0 = 1, a_1 = \frac{y_1 - y_0}{x_1 - x_0} \qquad 两点差商 \end{aligned}\]三点的二次插值多项式
\[P_2(x) = N_1(x) + a_2(x - x_0)(x - x_1) \triangleq N_2(x)\]满足$N_2(x_0) = y_0, N_2(x_1) = y_1$, 再由条件$N_2(x_2) = y_2$
\[y_0 + \frac{y_1 - y_0}{x_1 - x_0}(x - x_0) + a_2(x - x_0)(x - x_1) \triangleq N_2(x)\] \[\Rightarrow a_2 = \frac{(y_2 - y_0) - \frac{y_1 - y_0}{x_1 - x_0}(x_2 - x_1)}{(x_2 - x_0)(x_2 - x_1)} = \frac{\frac{y_2 - y_0}{x_2 - x_1} - \frac{y_1 - y_0}{x_1 - x_0}}{x_2 - x_0} \qquad 三点差商\]差商及性质
已知函数$f(x)$在$[a, b]$上的$n+1$个互异节点$x_0, x_1, …, x_n$处的函数值$f(x_0), f(x_1), …, f(x_n)$。 则:
\[f[x_i, x_j] \triangleq \frac{f(x_j) - f(x_i)}{x_j - x_i}\]称为$f(x)$关于节点$x_i, x_j$的一阶差商。
比如:
\[a_1 = \frac{y_1 - y_0}{x_1 - x_0} = \frac{f(x_1) - f(x_0)}{x_1 - x_0} = f[x_0, x_1]\]是$f(x)$关于节点$x_0, x_1$的一阶差商。
\[a_0 = y_0 = f[x_0]\]是$f(x)$关于节点$x_0$的零阶差商。
\[f[x_i, x_j, x_k] \triangleq \frac{f[x_j, x_k] - f[x_i, x_j]}{x_k - x_i}\]称为$f(x)$关于三个节点$x_i, x_j ,x_k$的二阶差商。
比如:
\[a_2 = \frac{\frac{y_2 - y_1}{x_2 - x_1} - \frac{y_1 - y_0}{x_1 - x_0}}{x_2 - x_0} = \frac{f[x_1, x_2] - f[x_0, x_1]}{x_2 - x_0} = f[x_0, x_1, x_2]\]一般地, 称:
\[f[x_0, x_1, ..., x_{k-1}, x_k] \triangleq \frac{f[x_1, ..., x_{k-1}] - f[x_0, x_1, ..., x_{k-1}]}{x_k - x_0}\]为$f(x)$关于节点$x_0, x_1, …, x_k$的$k$阶差商。
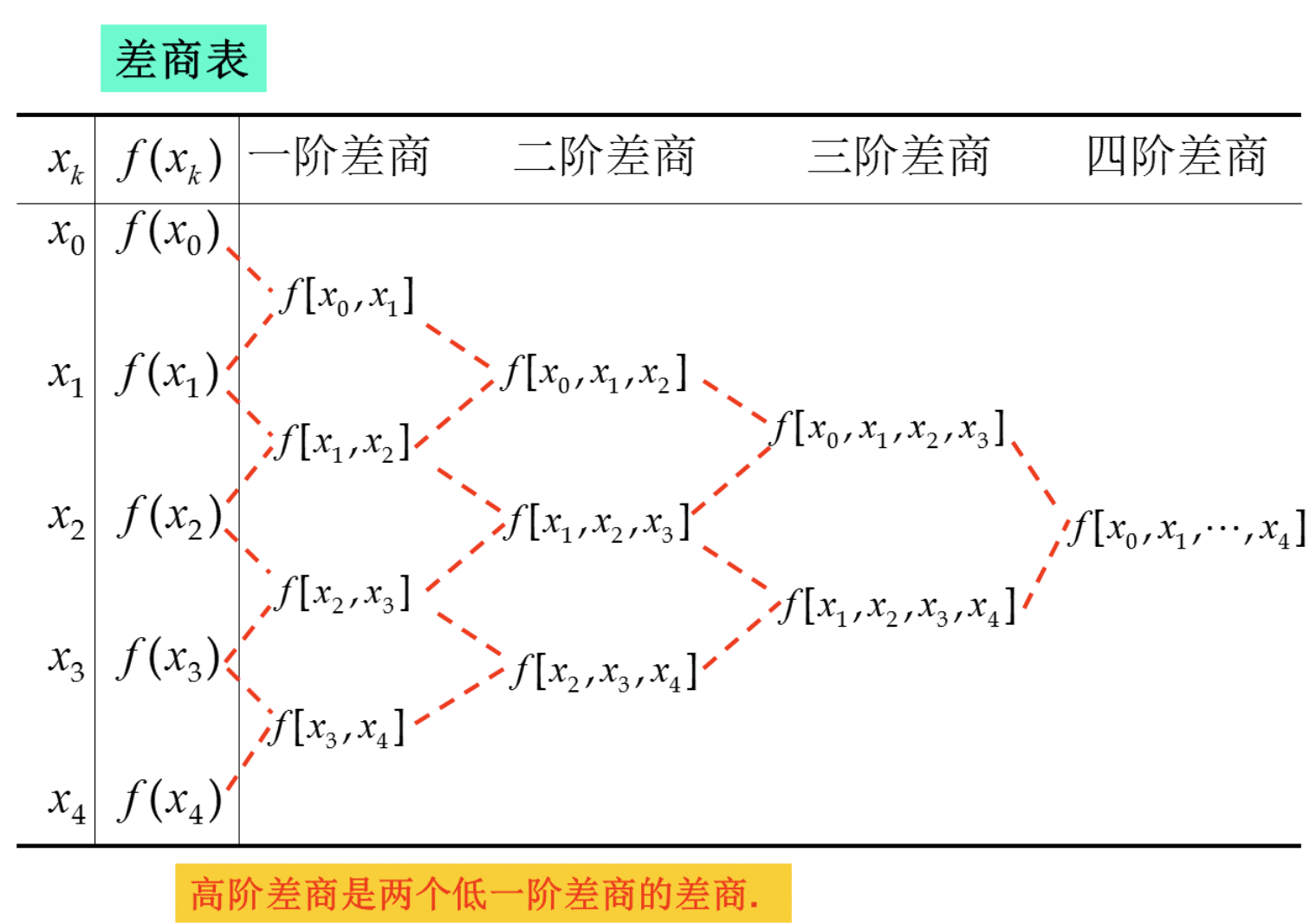
差商的性质
\[f[x_i, x_j] = \frac{f(x_j) - f(x_i)}{x_j - x_i} = \frac{f(x_i)}{x_i - x_j} + \frac{f(x_j)}{x_j - x_i} = \frac{1}{x_i - x_j} f(x_i) + \frac{1}{x_j - x_i}f(x_j)\] \[\begin{aligned} f[x_i, x_j, x_k] & = \frac{f[x_j, x_k] - f[x_i, x_j]}{x_k - x_i} = \frac{\frac{f(x_k) - f(x_j)}{x_k - x_j} - \frac{f(x_j) - f(x_i)}{x_j - x_i}}{x_k - x_i} \\ & = \frac{(f(x_k) - f(x_j))(x_j - x_i) - (f(x_j) - f(x_i))(x_k - x_j)}{(x_k - x_j)(x_j - x_i)(x_k - x_i)} \\ & = \frac{f(x_k)(x_j - x_i) - f(x_j)(x_j - x_i) - f(x_j)(x_k - x_j) + f(x_i)(x_k - x_j)}{(x_k - x_j)(x_j - x_i)(x_k - x_i)} \\ & = \frac{f(x_k)}{(x_k - x_j)(x_k - x_i)} - \frac{f(x_j)}{(x_k - x_j)(x_j - x_i)} + \frac{f(x_i)}{(x_j - x_i)(x_k - x_i)} \\ & = \frac{1}{(x_i - x_j)(x_i - x_k)}f(x_i) + \frac{1}{(x_j-x_k)(x_j - x_i)}f(x_j) + \frac{1}{(x_k - x_j)(x_k - x_i)}f(x_k) \end{aligned}\]性质1: 差商可用函数值线性表示。
$f(x)$的$k$阶差商可以表示成函数值$f(x_0), f(x_1), …, f(x_k)$的线性组合, 即
\[f[x_0, x_1, ..., x_{k-1}, x_k] = \sum_{i=0}^k \frac{f(x_i)}{(x_i - x_0)...(x_i - x_{i-1})(x_i - x_{i+1})...(x_i - x_k)}\]由性质1可知, 差商与节点的排列次序无关。
性质2: 差商具有对称性
差商与节点的排列次序无关, 即, 任意交换两个节点$x_i, x_j$的次序, 差商值不变。
\[\begin{aligned} f[x_0, x_1, ..., x_{k-1}, x_k] & = \frac{f[x_1, ..., x_{k-1}, x_k] - f[x_0, x_1, ..., x_{k-1}]}{x_k - x_0} \\ & = \frac{f[x_0, ..., x_{k-2}, x_k] - f[x_0, x_1, ..., x_{k-1}]}{x_k - x_{k-1}} \end{aligned}\]性质3: 差商与导数的关系
若$f(x)$在$[a, b]$上存在$k$阶导数,且节点
\[a \leq x_0 < x_1 < ... < x_{k-1} < x_k \leq b\]则$\exists \xi \in (a, b)$, 有:
\[f[x_0, x_1, ..., x_{k-1}, x_k] = \frac{f^{(k)}(\xi)}{k!}\]牛顿插值(Newton)公式及余项
根据差商定义,若$x$为$[a, b]$上的任意一点, 则: \(\begin{cases} f(x) = f(x_0) + f[x, x_0](x - x_0) \\ f[x, x_0] = f[x_0, x_1] + f[x, x_0, x_1](x - x_1) \\ f[x, x_0, x_1] = f[x_0, x_1, x_2] + f[x, x_0, x_1, x_2](x - x_2) \\ ... \\ f[x, x_0, ..., x_{n-1}] = f[x_0, ..., x_n] + f[x, x_0, ..., x_n](x - x_n) \end{cases}\)
思考: 这里和差商的定义有什么关系?
根据差商的定义, 若$x$视为$[a, b]$上的任意一点, 且$x \neq x_0$, 则:
\[f[x_0, x] = \frac{f(x) - f(x_0)}{x - x_0}\]从而
\[f(x) = f(x_0) + f[x, x_0](x - x_0)\]同理, 由:
\[f[x_0, x_1, x] = \frac{f[x_0, x] - f[x_0, x_1]}{x - x_1}\]可得:
\[f[x_0, x] = f[x_0, x_1] + f[x_0, x_1, x](x - x_1)\]依次求得
\[f[x_0, x_1, ..., x_{n-1}, x] = f[x_0, x_1, ..., x_n] + f[x_0, x_1, ..., x_n, x](x - x_n)\]将后一个式子代入前一个式子, 可得:
\[\begin{aligned} f(x) & = f(x_0) + f[x_0, x_1](x - x_0) + f[x_0, x_1, x_2](x - x_0)(x - x_1) + ...+ f[x_0, ..., x_n](x - x_0)...(x - x_{n-1}) \\ & + f[x, x_0, ..., x_n](x - x_0) ... (x - x_{n-1})(x - x_n) \end{aligned}\]即:
\[f(x) = N_n(x) + f[x_0, x_1, ..., x_n. x](x - x_0)(x - x_1)...(x - x_n)\]牛顿插值余项为:
\[\begin{aligned} R_n(x) & = f[x_0, x_1, ..., x_n, x](x - x_0)(x - x_1)...(x- x_n) \\ & = f[x_0, x_1, ..., x_n, x]\omega_{n+1}(x) \end{aligned}\]由于$R_n(x_i) = f(x_i) - N_n(x_i) = 0$, 即:
\[N_n(x_i) = f(x_i) (i=0, 1, ..., n)\]所以$N_n(x)$是$f(x)$的$n$次插值多项式, 从而
\[N_n(x) \equiv L_n(x)\] \[\Rightarrow R_n(x) = f[x, x_0, ..., x_n]\omega_{n+1}(x) = \frac{f^{(n+1)}(\xi_x)}{(n+1)!}\omega_{n+1}(x)\]推导出:
\[f[x_0, ..., x_k] = \frac{f^{(k)}(\xi)}{k!}, \xi \in (x_{min}, x_{max})\]牛顿插值多项式计算过程
1) 列差商表计算各阶差商, 求出牛顿插值系数$a_i$。
插值基函数$1, (x - x_0), (x - x_0)(x - x_1), …, (x - x_0)(x - x_1)…(x - x_n)$
牛顿插值多项式:
\[N_n(x) = f(x_0) + f[x_0, x_1](x - x_0) + f[x_0, x_1, x_2](x - x_0)(x - x_1) + ... + f[x_0, ..., x_n](x - x_0)...(x - x_{n-1})\]