引言
代数精度
如果当$f(x) = x^k \quad (k=0, 1, …, m)$时, 求积公式准确成立;而当$f(x) = x^{m+1}$时, 求积公式不准确成立, 称求积公式具有$m$次代数精度。
PS:
- (等价定义)定义1中$f(x) = x^k(k=0, 1, …, m)$改为:$f(x)$是次数不超过$m$的多项式
- 理论上,通过误差分析可以确定:用代数精度能够衡量求积公式的计算精度, 且$m$越大, 求积公式的绝对值误差$\mid E_n(f) \mid$也越小。
例:
$n=0$时, $\int_a^b f(x)dx \approx A_0 f(x_0) = (b - a)f(x_0)$
上面由积分中值定理推得, 矩形公式
若取$x_0 = a$, 为左矩形公式
若取$x_0 = b$, 为右矩形公式
$x_0 = \frac{a+b}{2}$, 为中矩形公式
$n=1$时, 若取$x_0 = a, x_1 = b, A_0 = A_1 = \frac{b - a}{2}$
\[\int_a^b f(x) dx \approx A_0f(x_0) + A_1f(x_1) = \frac{b-a}{2}[f(a) + f(b)]\]上式为梯形公式。
将$f(x) = 1$代入$\int_a^b f(x)dx \approx A_0 f(x_0) = (b - a)f(x_0)$, 准确成立
将$f(x) = x$代入$\int_a^b f(x)dx \approx A_0 f(x_0) = (b - a)f(x_0)$, $\frac{1}{2}(b^2 - a^2) \neq (b - a)x_0$
因此左矩形公式、右矩形公式具有0次代数精度, 中矩形公式具有1次代数精度。
插值型求积公式及其性质
数值积分公式
一般形式:
\[I(f) \triangleq \int_a^b \rho(x)f(x)dx \approx \sum_{i=0}^n A_i f(x_i) \triangleq I_n(f)\]插值型:
\[\int_a^b \rho(x)f(x)dx \approx \int_a^b \rho(x)L_n(x)dx = \sum_{i=0}^n A_if(x_i)\]其中:
\[A_i = \int_a^b \rho(x)l_i(x)dx (i=0, 1, ..., n)\]误差:
\[E_n(f) = \int_a^b \rho(x)\frac{f^{(n+1)(\xi)}}{(n+1)!} \prod_{i=0}^n(x - x_i)dx\]牛顿——科特斯公式及余项估计
牛顿——科特斯(Newton-Cotes)公式
权函数$\rho(x) \equiv 1$, 将区间 [a, b] n等分, 步长$h = \frac{b - a}{n}$, 等距节点$x_i = a + ih(i = 0 \thicksim n)$
令$x = a + th$, 则Lagrange插值基函数为:
\[l_i(x) = \prod_{j=0, j \neq i}^n\frac{x - x_j}{x_i - x_j} = \prod_{j=0, j \neq i}^n \frac{t - j}{i - j} \qquad (i = 0 \thicksim n)\]故求积系数为(记住吧):
\[A_i = \int_a^b l_i(x)dx = \frac{(-1)^{n-i}h}{i!(n-i)!}\int_0^n \prod_{j=0, j \neq i}^n(t - j)dt \qquad (i=0 \thicksim n)\]令
\[C_i^{(n)} = \frac{A_i}{b-a} = \frac{A_i}{hn}= \frac{(-1)^{n-i}}{i!(n-i)!n}\int_0^n \prod_{j=0, j \neq i}^n (t - j)dt\]称Cotes系数。
故:
\[A_i = (b - a)C_i^{(n)} \qquad (i=0, 1, 2, ..., n)\]则求积公式
\[\int_a^b f(x) dx \approx (b - a)\sum_{i=0}^n C_i^{(n)}f(x_i)\]称为n阶Newton-Cotes公式
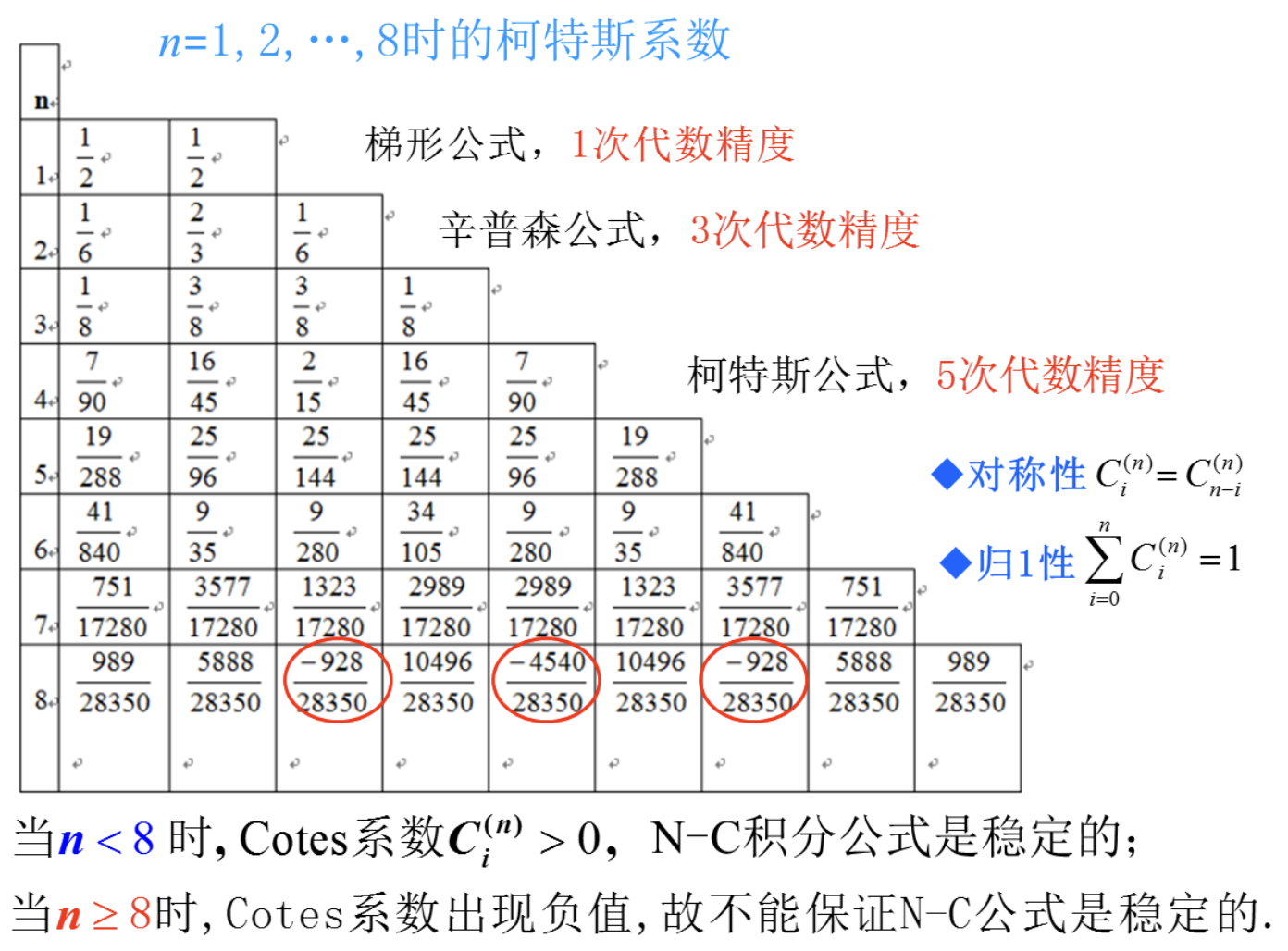
Cotes系数与$f(x), [a, b]$无关, 仅与$n, i$有关。
几个低阶的Newton-Cotes公式
梯形公式
当$n=1$时, $2$个节点Cotes系数为$C_0^{(1)} = C_1^{(1)} = \frac{1}{2}$
求积公式:
\[\int_a^b f(x)dx \approx \frac{b - a}{2} [f(a) + f(b)] \triangleq T(f)\]称为梯形公式, 代数精度为1.
辛普森(Simpson)公式
当$n = 2$时, $3$个节点, 步长$h = \frac{b - a}{2}$
Cotes系数为
\(C_0^{(2)} = \frac{(-1)^{2 - 0}}{2·0!·2!}\int_0^2(t-1)(t-2)dt = \frac{1}{6}\),
\[C_1^{(2)} = \frac{(-1)^{2 - 1}}{2·1!·(2-1)!}\int_0^2t(t-2)dt = \frac{4}{6}\] \[C_2^{(2)} = \frac{(-1)^{2 - 2}}{2·2!·(2-2)!}\int_0^2t(t-1)dt = \frac{1}{6}\]求积公式:
\[\int_a^b f(x)dx \approx \frac{b-a}{6}[f(a) + 4f(\frac{a+b}{2}) + f(b)] \triangleq S(f)\]称为Simpson公式,代数精度为3.
Simpson公式的几何意义是, S恰好是经过三点
\[(a, f(a)), (\frac{a+b}{2}, f(\frac{a+b}{2})), (b, f(b))\]的抛物线所围成的曲边梯形的面积
科特斯(Cotes公式)
当$n=4$时,5个节点, 步长$h = \frac{b-a}{4}$
Cotes系数为$C_0^{(4)} = \frac{7}{90}, C_1^{(4)} = \frac{32}{90}, C_2^{(4)} = \frac{12}{90}, C_3^{(4)} = \frac{32}{90}, C_4^{(4)} = \frac{7}{90}$
求积公式:
\[\int_a^b f(x)dx \approx \frac{b - a}{90}[7f(a) + 32f(x_1) + 12f(x_2) + 32f(x_3) + 7f(b)] \triangleq C(f)\]称为Cotes公式, 代数精度为5
例:
分别用梯形公式、Simpson公式、Cotes公式计算积分
\[I = \int_{0.5}^1 \sqrt{x} dx\]解:
梯形公式:
当$n=1$时, $2$个节点Cotes系数为$C_0^{(1)} = C_1^{(1)} = \frac{1}{2}$
求积公式:
\[\int_a^b f(x)dx \approx \frac{b - a}{2} [f(a) + f(b)] = \frac{1 - 0.5}{2}(\sqrt{0.5} + \sqrt{1}) \approx 0.42677670\]Simpson公式:
当$n = 2$时, $3$个节点, 步长$h = \frac{b - a}{2}$
Cotes系数为
\[C_0^{(2)} =\frac{(-1)^{2 - 0}}{2·0!·2!}\int_0^2(t-1)(t-2)dt = \frac{1}{6}\] \[C_1^{(2)} = \frac{(-1)^{2 - 1}}{2·1!·(2-1)!}\int_0^2t(t-2)dt = \frac{4}{6}\] \[C_2^{(2)} = \frac{(-1)^{2 - 2}}{2·2!·(2-2)!}\int_0^2t(t-1)dt = \frac{1}{6}\]求积公式:
\[\int_a^b f(x)dx \approx \frac{b-a}{6}[f(a) + 4f(\frac{a+b}{2}) + f(b)] = \frac{1 - 0.5}{6}[\sqrt{0.5} + 4\sqrt{0.75} + \sqrt{1}] \approx 0.43093403\]Cotes公式:
Cotes系数为$C_0^{(4)} = \frac{7}{90}, C_1^{(4)} = \frac{32}{90}, C_2^{(4)} = \frac{12}{90}, C_3^{(4)} = \frac{32}{90}, C_4^{(4)} = \frac{7}{90}$
求积公式:
\[\int_a^b f(x)dx \approx \frac{b - a}{90}[7f(a) + 32f(x_1) + 12f(x_2) + 32f(x_3) + 7f(b)] = \frac{0.5}{90}(7\sqrt{0.5} + 32\sqrt{0.625} + 12\sqrt{0.75} + 32\sqrt{0.875} + 7\sqrt{1}) \approx 0.43096407\]偶数阶N-C公式的代数精度
因为N-C公式是插值型求积公式, 故$n$阶N-C公式至少具有$n$次代数精度。
定理1: 当$n$为偶数时, 牛顿-科特斯公式:
\[\int_a^b f(x) dx \approx (b-a)\sum_{i=0}^n C_i^{(n)}f(x_i)\]至少具有$n+1$代数精度。
Newton-Cotes公式的积分余项
第一积分中值定理:
条件:
- $f(x), g(x)$在闭区间$[a, b]$上可积
- $g(x)$在$[a, b]$上不变号
- $f(x)$连续
结论:在积分区间$[a, b]$上至少存在一点$\xi$, 使$\int_a^b f(x)g(x)dx = f(\xi)\int_a^b g(x)dx$
梯形公式的积分余项
\[E_T(f) = I(f) - T(f) = \int_a^b \frac{f''(\xi)}{2!}(x - a)(x - b)dx\]设$f’‘(x) \in C^2[a, b]$, 由于$g(x) = (x - a)(x - b)$在区间$[a, b]$上不变号, 根据第一积分中值定理, 存在$\eta \in [a, b]$, 使:
\[E_T(f) = -\frac{(b-a)^3}{12}f''(\eta) = -\frac{h^3}{12}f''(\eta)\]其中步长$h = b - a$
Simpson公式的积分余项
\[\begin{aligned} E_s(f) & = I(f) - S(f) \\ & = \int_a^b \frac{f^{(4)}(\xi)}{4!}(x - a)(x - \frac{a+b}{2})(x - b)dx \\ & = -\frac{b - a}{180} (\frac{b-a}{2})^4 f^{(4)}(\eta) \\ & = -\frac{h^5}{90}f^{(4)}(\eta), \qquad \eta \in [a, b] \end{aligned}\]其中步长$h = \frac{b-a}{2}, f^{(4)}(x) \in C^4[a, b]$
Cotes公式的积分余项
\[\begin{aligned} E_c(f) & = I(f) - C(f) \\ & = -\frac{2(b - a)}{945}(\frac{b-a}{4})^6 f^{(6)}(\eta) \\ & = -\frac{2(b - a)}{945}h^6f^{(6)}(\eta), \qquad \eta \in [a, b] \end{aligned}\]其中步长$h = \frac{b - a}{4}$, $f^{(6)}(x) \in C^6[a, b]$
一般的N-C公式的积分余项
定理2: 设$f(x) \in C^{n+2}[a, b]$(k是正整数)
若$n$为偶数, 则积分余项
\[R_n(f) = \frac{h^{n+3}f^{n+2}(\eta)}{(n+2)!}\int_0^n t^2(t-1)...(t - n)dt, \quad \eta \in [a, b]\]若$n$为奇数, 则积分余项
\[R_n(f) = \frac{h^{n+2}f^{(n+1)}(\eta)}{(n+1)!}\int_0^n t(t-1)...(t-n)dt, \quad \eta \in [a, b]\]复化(合)求积公式
常用的两种求积公式作复化求积
梯形公式$T = \frac{b-a}{2}[f(a) + f(b)]$
积分余项: $E_T = -\frac{(b-a)^3}{12}f’’(\eta), \quad \eta \in [a, b]$
代数精度: 1次代数精度
辛普森公式$S = \frac{b-a}{6}[f(a) + 4f(\frac{a+b}{2}) + f(b)]$
积分余项: $E_s = - \frac{b-a}{180}(\frac{b-a}{2})^4f^{(4)}(\eta)$
代数精度: 3次代数精度
复化梯形公式
将$[a, b]$等分成$n$个区间, $h = \frac{b-a}{n}$, $x_i = a + ih, i = 0 \thicksim n$
在每个子区间上使用梯形公式
\[\int_{x_i}^{x_{i+1}}f(x)dx = \frac{h}{2}[f(x_i) + f(x_{i+1})] - \frac{h^3}{12}f''(\xi_i), \quad x_i < \xi_i < x_{i+1}\]则:
\[\begin{aligned} I & = \int_a^b f(x)dx = \sum_{i=0}^{n-1} \{\frac{h}{2}[f(x_i) + f(x_{i+1})] - \frac{h^3}{12}f''(\xi_i)\} \\ & = \frac{h}{2}[f(a) + 2\sum_{i=1}^{n-1}f(x_i) + f(b)] - \frac{h^3}{12}\sum_{i=0}^{n-1}f''(\xi_i) \\ & = \frac{h}{2}[f(a) + 2\sum_{i=1}^{n-1}f(a + ih) + f(b)] - \frac{b - a}{12}h^2f''(\xi) \\ & = T_n + E_{T_n} \end{aligned}\]复化Simpson公式
将$[a, b]$分成$n$个区间, $h = \frac{b - a}{n}$, 在每个子区间$[x_k, x_{k+1}]$上使用辛普森公式, 记区间中点$x_{k+1/2}$, 得
\[\begin{aligned} I & = \int_a^b f(x)dx = \sum_{k=0}^{n-1}\int_{k=0}^{n-1}f(x)dx \\ & = \sum_{k=0}^{n-1}\{\frac{h}{6}[f(x_k) + 4f(x_{k+1/2}) + f(x_{k+1})] - \frac{h}{180}(\frac{h}{2})^4 f^{(4)}(\xi_k)\} \end{aligned}\]记
\[\begin{aligned} S_n & = \frac{h}{6}\sum_{j=0}^{n-1}[f(x_k) + 4f(x_{k+1/2}) + f(x_{k+1})] \\ & = \frac{h}{6}[f(a) + 4\sum_{k=0}{n-1}f(x_{k+1/2}) + 2\sum_{k=1}^{n-1}f(x_k) + f(b)] \end{aligned}\]为复化辛普森求积公式

例:
应用复合梯形公式计算积分:$I = \int_0^1 6e^{-x^2}dx$, 要求误差不超过$10^{-6}$, 试确定所需的步长和节点个数。
解:
令$f(x) = 6 e^{-x^2}$, 则$f’(x) = -12xe^{-x^2}$, $f’‘(x) = 12e^{-x^2}(2x^2 - 1)$, $f’’’^{x} = 24xe^{-x^3}(3 - 2x^2) \neq 0, x \in (0,1)$
由于$f’‘(x)$在$[0,1]$上为单调函数, 所以:
\[\max_{x \in [0, 1]}\mid f''(x) \mid = \max\{\mid f''(0) \mid, \mid f''(1) \mid\} = \max\{\mid -12 \mid, \mid 12e^{-1} \mid\} = 12\]由复化梯形的误差公式:
\[\begin{aligned} E_n(f) & = -\frac{h^2(1 - 0)}{12} f''(\xi), 0 < \xi < 1 \\ & \Rightarrow \mid E_n(f) \mid \leq \frac{h^2}{12} \max_{x \in [0, 1]}\mid f''(x) \mid \end{aligned}\]要使$\mid E_n(f) \mid \leq 10^{-6} \Rightarrow h \leq 10^{-3}$
取$h = 10^{-3}$, 由$h = \frac{b - a}{n} = \frac{1}{n} \Rightarrow n = 10^3$
故可取节点数为1001
龙贝格(Romberg)积分法
梯形法的逐次半分递推公式
将区间$[a, b]$ n等分, 节点$a = x_0 < x_1 < … < x_{n-1} < x_n = b$, 记$x_i = a + ih (i = 0 \thicksim n)$, 步长$h = \frac{b - a}{n}$, 则复化梯形公式:
\[T_n = \sum_{i=0}^{n-1} \frac{h}{2} [f(x_i) + f(x_{i+1})]\]在每个子区间$[x_i, x_{i+1}]$上取重点$x_{i + \frac{1}{2}} = \frac{1}{2}(x_i + x_{i+1}), i=0 \thicksim n-1$, 将区间$[a, b]$半分成了$2n$等分。
每个子区间$x_i, x_{i+1}$上的积分应用复化梯形公式, 计算的
\[\frac{h}{4}[f(x_i) + 2f(x_{i + 1/2}) + f(x_{i+1})]\]$h$是二分前的步长
各子区间上复化梯形值相加, 求得半分后的复化梯形值为
半分后:
\[T_{2n} = \frac{h}{4} \sum_{i=0}^{n-1}[f(x_i) + f(x_{i+1})] + \frac{h}{2} \sum_{i=0}^{n-1}f(x_{i+1/2})\]半分前:
\[T_n = \sum_{i=0}^{n-1}\frac{h}{2}[f(x_i) + f(x_{i+1})]\]则
\[T_{2n} = \frac{1}{2}T_n + \frac{h}{2}\sum_{i=0}^{n-1}f(x_{i + 1/2})\]梯形法的半分递推公式, 也称为变步长的梯形公式
龙贝格(Romberg)算法
首先 根据复合梯形法求积公式的余项
\[I - T_n = -\frac{b-a}{12}h^2f''(\xi_n), \quad \xi_n \in (a, b)\] \[I - T_{2n} = -\frac{b-a}{12} (\frac{h}{2})^2 f''(\xi_{2n}), \quad \xi_{2n} \in (a, b)\]当$f’‘(x) \in C[a, b]$, 且$n$充分大时$f’’(\xi_n) \approx f’’(\xi_{2n})$, 有:
\[I - T_{2n} \approx -\frac{b - a}{12} (\frac{h}{2})^2 f''(\xi_)\]由逐次二分公式
\[\begin{cases} T_1 = \frac{b - a}{2}[f(a) + f(b)] \\ T_{2^k} = \frac{1}{2}T_{2^{k-1}} + \frac{b-a}{2^k} \end{cases}\]高斯型求积公式
$[-1, 1]$上两点的高斯公式:
\[\int_{-1}^1 f(x)dx \approx f(-\frac{1}{\sqrt{3}}) + f(\frac{1}{\sqrt{3}})\]若$t \in [-1, 1]$, 那么$x \in [a, b]$
\[x = \frac{b-a}{2}t + \frac{a+b}{2}\]$[a, b]$上的两点高斯公式:
\[\begin{align} \int_a^b f(x)dx &= \frac{b - a}{2} \int_{-1}^1 f(\frac{b-a}{2}t + \frac{a+b}{2})dt \\ &\approx \frac{b-a}{2}[f(-\frac{b-a}{2\sqrt{3}} + \frac{a+b}{2}) + f(\frac{b-a}{2\sqrt{3}} + \frac{a+b}{2})] \end{align}\]因此
\[A = B = \frac{b-a}{2}, x_0 = -\frac{b-a}{2\sqrt{3}} + \frac{a + b}{2}, x_1 = \frac{b - a}{2\sqrt{3}} + \frac{a+b}{2}\]