符号表示
- $x_t$: $t$时刻的输入
- $s_{t-1}$: 上一时刻的状态
- $z$: $z = Vs_t$
- $U$: $x_t$的权重矩阵
- $W$: $s_{t-1}$的权重矩阵
- $V$: $s_t$的权重矩阵
- $E$: 表示损失函数
softmax求导
\[a_j = \frac{e^{z_j}}{\sum_k e^{z_k}}\]当$i = j$的时候:
\[\begin{aligned} \frac{\partial a_j}{\partial z_i} &= \frac{\partial}{\partial z_i} (\frac{e^{z_j}}{\sum_k e^{z^k}}) \\ &= \frac{(e^{z_j})'·\sum_k e^{z_k} - e^{z_j}·e^{z_j}}{(\sum_k e^{z_k})^2} \\ &= \frac{e^{z_j}}{\sum_k e^{z_k}} - \frac{e^{z_j}}{\sum_k e^{z_k}}·\frac{e^{z_j}}{\sum_k e^{z_k}} \\ &= a_j(1-a_j) \end{aligned}\]当$i \neq j$的时候
\[\begin{aligned} \frac{\partial a_j}{\partial z_i} &= \frac{\partial}{\partial z_i} (\frac{e^{z_j}}{\sum_k e^{z^k}}) \\ &= \frac{(e^{z_j})'·\sum_k e^{z_k} - e^{z_j}·e^{z_i}}{(\sum_k e^{z_k})^2} \\ &= -\frac{e^{z_j}}{\sum_k e^{z_k}} · \frac{e^{z_i}}{\sum_k e^{z_k}} = -a_j · a_i \end{aligned}\]交叉熵求导
\[E_t(y_t, \hat y_t) = -y_t log \hat y_t\] \[E(y, \hat y) = \sum_t E_t(y_t, \hat y_t) = \sum_t -y_t log \hat y_t\] \[\begin{aligned} \frac{\partial E}{\partial \hat y_i} = \sum_t -\frac{y_t}{\hat y_t} \end{aligned}\]RNN的BPTT过程
RNN的公式:
\[s_t = tanh(Ux_t + W s_{t-1})\] \[\hat y_t = softmax(V s_t)\]预测结果$\hat y_t$与正确结果$y_t$做交叉熵得到损失值:
\[E_t(y_t, \hat y_t) = -y_t log \hat y_t\] \[\begin{aligned} E(y, \hat y) &= \sum_t E_t(y_t, \hat y_t) \\ &= -\sum_t y_t log \hat y_t \end{aligned}\]在每个timestep,如果是做序列标注任务,我们每一个时刻都会预测一个结果,并得到一个损失值,那么最终的损失将会是所有时刻损失之和,如下所示:
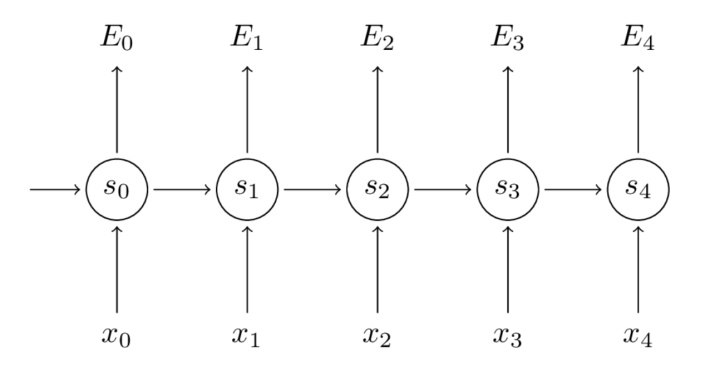
总的损失表示为:
\[\frac{\partial E}{\partial W} = \sum_t \frac{\partial E_t}{\partial W}\]下面以第3时刻为例,其它位置均为相同操作。
首先求对参数 $V$ 进行求导, 过程如下:
\[\begin{aligned} \frac{\partial E_3}{\partial V} &= \frac{\partial E_3}{\partial \hat y_3} \frac{\partial y_3}{\partial V} \\ &= \frac{\partial E_3}{\partial \hat y_3} \frac{\partial \hat y_3}{\partial z_3} \frac{\partial z_3}{\partial V} \\ &= [-\frac{y_3}{\hat y_3} · \hat y_3(1- \hat y_3) - \sum_{i \neq 3, i=0}^4 \frac{y_i}{\hat y_i}(-\hat y_i \hat y_3)] · s_3 \\ &= [-y_3(1 - \hat y_3) + \sum_{i \neq 3, i=0}^4 y_i \hat y_3] · s_3 \\ &= [-y_3 + y_3 \hat y_3 + \sum_{i \neq 3, i=0}^4 y_i \hat y_3] · s_3 \\ &= [-y_3 + \hat y_3 \sum_{i=0}^4 y_i] · s_3 \\ &= (\hat y_3 - y_3) · s_3 \end{aligned}\]下面对W进行求导:
\[\frac{\partial E_3}{\partial W} = \frac{\partial E_3}{\partial \hat y_3} \frac{\partial \hat y_3}{\partial s_3} \frac{\partial s_3}{\partial W}\]但是其中的$s_3 = tanh(Ux_3 + Ws_2)$, $s_3$依赖于$s_2$和$W$, 这个时候不能简单地把$s_3$当做常数看待, 继续使用链式法则:
\[\begin{aligned} \frac{\partial E_3}{\partial W} &= \frac{\partial E_3}{\partial \hat y_3} \frac{\partial \hat y_3}{\partial s_3} \frac{\partial s_3}{\partial W} \\ &= \frac{\partial E_3}{\partial \hat y_3} \frac{\partial \hat y_3}{\partial s_3}(\frac{\partial s_3}{\partial s_3}\frac{\partial s_3}{\partial W} + \frac{\partial s_3}{\partial s_2}\frac{\partial s_2}{\partial W} + \frac{\partial s_3}{\partial s_1}\frac{\partial s_1}{\partial W} + \frac{\partial s_3}{\partial s_0}\frac{\partial s_0}{\partial W}) \end{aligned}\]合成公式为:
\[\frac{\partial E_3}{\partial W} = \sum_{k=0}^3 \frac{\partial E_3}{\partial \hat y_3} \frac{\partial \hat y_3}{\partial s_3} \frac{\partial s_3}{\partial s_k} \frac{\partial s_k}{\partial W}\]对U求导和对S求导完全一样!