Abstract
我们提出了一种使用单个深度神经网络检测图像中物体的方法。我们的方法叫做SSD,在每个特征映射位置不同宽高比和尺度上, 离散化bboxes的输出空间到一组默认的boxes。在预测时, 网络在每个默认的box中对每个物体种类的出现生成分数, 并且对box产生调整以更好地适应物体形状。此外, 网络结合从多个特征图使用不同分辨率的预测去自然地处理不同尺寸的物体。SSD相较于需要物体提议的方法是相对简单的, 因为它彻底消除了提议产生和随后的像素或特征重采样阶段, 并且封装进了单个网络。
结果:
- 300x300 的输入, SSD在Titan X 上 VOC2007 test上取得74.3% mAP以及59FPS。
- 512x512 的输入, SSD取得了76.9%的mAP, 超出了SOTA Faster R-CNN
Introduction
当前SOTA物体检测系统是以下方式的变体:假设bboxes, 为每个box重采样像素或特征, 再使用一个高质量的分类器。这种pipeline在检测benchmarks上很流行是因为这些结果在PASCAL VOC, COCO和ILSVRC检测上都基于Faster R-CNN。通常这些方法的检测速度衡量标准是每帧多少秒(SPF), 即便是最快的检测器Faster R-CNN执行做到一秒7帧(FPS)。
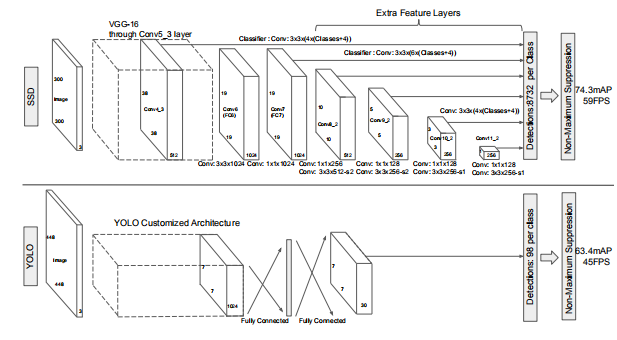
SSD的结果在高准确率的检测前提下,显著地提高了速度(在VOC2007 test上74.3%mAP, 59FPS, Faster R-CNN 73.2% mAP 7FPS, YOLO 63.4mAP 45FPS 。在速度上最基础的提升来自于消除了bbox proposals和接下来的像素或特征重采样阶段。
我们的提升包括:
- 使用小的卷积核去预测物体种类以及bbox位置的误差
- 对不同长宽比的检测器使用分离的预测器(filters)
- 并且将这些filters用在网络接下来阶段的多个特征图上以实现多尺度的检测
有了这些修改,尤其是在不同尺度上使用多层预测, 我们可以使用相对小的分辨率输出取得高准确率, 进一步增加检测速度。尽管这些贡献似乎很小, 却使得系统在实时检测上提升了对PASCAL VOC准确率, 将YOLO 63.4% mAP 提升到了我们SSD的74.3% mAP。
我们总结了我们的贡献如下:
- 我们引入了SSD, 一个比SOTA 单样本检测(YOLO)更快的多种类的单样本检测器。
- SSD对一个固定的默认bboxes集合预测种类分数和的box误差的核心是使用小的卷积核到特征图上。
- 为了取得高准确率, 我们从不同尺度的特征图中产生不同尺度的预测, 并且通过不同比例利用分离的预测。
- 这些设计的特征导致简单的端到端训练以及高准确率, 即便输入低分辨率图像, 进一步提升了准确率和速度之间的权衡。
- 在PASCAL VOC、COCO和ILSVRC上使用不同大小的输入, 进行了包括时间和准确率的模型的分析实验, 并且和大量的SOTA方法进行了比较。
The Single Shot Detector (SSD)
Model
SSD方法时基于一个前馈卷积网络, 它为在这些boxes的物体种类实例产生一个固定尺寸bboxes集合, 然后统计非极大值抑制步骤产生最终的检测结果。前面的层基于用于高质量图像分类的标准结构(分类层之前), 我们称之为基础网络。 我们然后用以下特点添加辅助结构产生检测结果:
为检测使用多尺度特征图 我们增加一个卷积特征曾到基础网络的最后。 这些层逐步减少了尺寸并允许在多尺度检测的预测。对于每个特征层, 卷积模型预测检测结果是不同的(Overfeat和YOLO在单尺度特征图上运行)。
用于检测的卷积预测器 每个添加的特征层(或者可选择的从基础网络中存在的特征层)能够使用一组卷积核产生一组固定检测预测。这些由图2中的SSD网络结构的顶部预测。对于一个尺寸大小为m x n, p个通道的特征层, 用于预测潜在检测的参数的基础元素是一个3 x 3 x p 的小卷积核, 它为一个种类产生一个分数, 同时也对默认框产生一个形状误差。 在每个用到卷积核的m x n位置, 它产生一个输出值。 bbox误差输出值 由 默认框的位置和特征图位置 测量得到(YOLO的结构使用了一个中间的全连接网络而不是在这一步使用卷积核)。
默认框核宽高比 我们为每个特征图设置了一组默认框, 在网络的最顶层的多个特征图。默认框用卷积的方式核特征图联系在一起, 因此每个box核特征图的关系时固定的。 在每个特征图上, 我们在特征图上预测默认框的误差, 同时我们在这些框里预测每个实例的种类, 并为它们打分。 特别地, 在一个给定位置k的每个框, 我们计算c类分数核4个相对于原始默认框形状的误差。这个结果总共 (c + 4)k 个卷积核 用在特征图的每个位置上, 对于一个m x n 的特征图, 产生 (c + 4)kmn 个输出。我们的默认框类似于Faster R-CNN 中的 anchor boxes, 然而我们使用它们在不同分辨率的多个特征图上。 使得不同默认框形状在多个特征图让我们有效地离散化box形状输出可能的空间。
Training
在训练SSD和训练一个典型的使用区域提议的检测器的关键不同是真实信息需要被用于在一组固定检测器输出的指定输出。一些版本也被用于训练YOLO以及Faster R-CNN和MultiBox的区域提议阶段。一旦这个 分配确定, 损失函数和反向传播用于端到端。 训练也包含为检测选择一组默认框和尺度同时hard negative mining和数据增强策略。
Matching strategy 在训练时我们需要决定那个默认框和真实检测相联系以及有根据地训练网络。 对于每个真实框我们对所有位置, 宽高比和尺度选择不同的默认框。我们最好的jaccard overlap匹配真实框和默认框。 我们将默认框和真实框的jaccard overlap阈值设置为0.5. 这简化了学习问题, 使得网络对于多个overlapping默认框预测高的分数而不是需要它选择仅仅一个最大的overlap。
训练目标 SSD的训练目标来自于MultiBox的训练目标, 但是拓展成了处理多目标种类。 让 $x_{ij}^p$ 表示第 $i$ 个默认框匹配 种类 $p$ 的第 $j$ 个真实框的指示器。 在上述的匹配策略中, 我们让 $\sum_i x_{ij}^p \geq 1$。 全部的目标损失函数时位置损失和置信度损失的加权和:
\[L(x, c, l, g) = \frac{1}{N}(L_{conf}(x, c) + \alpha L_{loc}(x, l, g)) \tag{1}\]其中 $N$ 是匹配的默认框的数量。 如果 $N = 0$, 我们设置损失为0。位置损失是预测框( $l$ ) 和 真实框( $g$ ) 之间的 Smooth L1 损失 。 和Faster R-CNN一样, 我们为默认框( $d$ )中心 ( $cx, cy$ ) 和它的宽( $w$ )和高( $h$ )回归误差。
\[L_{loc}(x, l, g) = \sum^N_{i \in \text{Pos m}\in {cx, cy, w, h}} \sum x_{ij}^k smooth_{L1}(l_i^m - \hat g_j^m) \\ \hat g_j^{cx} = (g_j^{cx} - d_i^{cx}) / d_i^w \qquad \hat g_j^{cy} = (g_j^{cy} - d_i^{cy}) / d_i^h \\ \hat g_j^w = log(\frac{g_j^w}{d_i^w}) \qquad g_j^h = log(\frac{g_j^h}{d_i^h}) \tag{2}\]置信度损失是对所有多个种类置信度的softmax损失:
\[L_{conf}(x, c) = -\sum_{i \in Pos}^N x_{ij}^p log(\hat c_i^p) - \sum_{i \in Neg} log (\hat c_i^0) \\ where \quad \hat c_i^p = \frac{exp(c_i^p)}{\sum_p exp(c_i^p)} \tag{3}\]权重项$\alpha$由交叉验证设置为1。
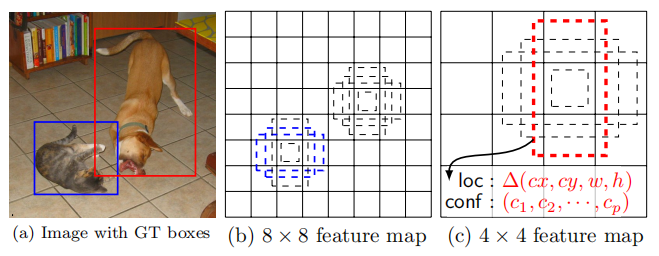
为默认框选择尺度和宽高比 为了处理不同目标的尺度, 一些方法提出在不同尺寸处理图像以及之后组合这些结果。 然而, 通过利用来自多个不同层的特征图在单个神经网络中我们可以模仿出相同的效果, 同时对所有物体尺度共享参数。 之前的工作表明使用低层的特征图能够提升语义分割质量, 因为低层捕获更多输入物体的微小的细节。 相似的, 一些工作表明添加从特征图池化的全局信息能偶帮助光滑语义分割结果。受到这些方法的启发, 我们同时用低和高层特征图来检测。 图1展示了用在框架中的两种特征图(8 x 8 和 4 x 4) 。
在一个框架不同等级的特征图有不同的感受野大小。 幸运的是, 在SSD框架中, 默认框不是非要和每层的真实感受野相联系。我们设计默认框的关系使得在特定的特征图学习和特定的物体的尺度项联系。 假设我们想要使用 $m$ 特征图用于预测。默认框相对于每个特征图的尺度可以被计算为:
\[s_k = s_{min} + \frac{s_{max} - s_{min}}{m-1}(k - 1), \qquad k \in [1, m] \tag{4}\]其中 $s_{min}$ 是 0.2, $s_{max}$是0.9, 意味着最低的层尺度为0.2, 最高的层尺度为0.9, 所有在之间的层有规律地递进。 我们为默认框施加不同宽高比, 表示它们为$a_r \in {1, 2, 3, \frac{1}{2}, \frac{1}{3}}$。 我们可以计算宽度( $w_k^\alpha = s_k \sqrt{a_r}$ ) 和 高度 ($h_k^a = s_k / \sqrt{a_r}$)对每一个默认框。 对于宽高比1, 我们增加了一个默认框, 它的尺度为$s’k = \sqrt{s_k s{k+1}}$, 每个特征图位置产生 6 个默认框。 我们设置每个默认框的中心为 $(\frac{i + 0.5}{\mid f_k \mid}, \frac{j + 0.5}{\mid f_k \mid})$, 其中$\mid f_k \mid$是第k个特征图地尺寸, $i, j \in (0, \mid f_k \mid)$。 事实上, 我们可以设计默认框地分布以最好地适应一个指定地数据集。 如何设计最有地关系也是一个开放的问题。
通过组合来自于不同特征图的所有位置在不同尺度和宽高比所有默认框的预测, 我们有一个有差异的预测集合, 覆盖不同的输入尺寸和形状。 比如, 在图1, 狗匹配到在 4 x 4 特征图中的一个默认框, 但是没有任何默认框在 8 x 8特征图中。 这是因为这些框有不同的尺度并且不会匹配狗框, 因此在训练时被考虑为负样本。
Hard negative mining 在匹配步骤之后, 大部分的默认狂是负的, 尤其是可能是默认框的数量是巨大的。 这在正样本和负样本之间引入了一个显著的不平衡。 我们不使用所有的负样本, 我们为每个默认框使用最高的置信度来排序, 然后选择最高的那个, 因此这样负样本和正样本的比例是3:1. 我们发现这使得更快的优化以及更稳定的训练。
数据增强 为了使得模型更加健壮对于不同输入目标的尺寸以及形状, 每个训练图像随机由下列选项之一采样:
- 使用整个原始输入图像
- 采样一个小块, 一边最小的 jaccard overlap为0.1, 0.3, 0.5, 0.7或者0.9
- 随机采样一个patch
随机采样的path尺寸为 原始尺寸的$[0.1, 1]$, 并且宽高比为 $\frac{1}{2}$和$2$之间。 如果 真实框的中心在我们采样的patch之中, 我们保持真实框重叠的部分。 在上述的采样步骤之后, 每个采样块被调整为固定的尺寸, 以0.5的概率水平翻转, 此外还是用了一些图像标准的扭曲。