Word Embedding (word2vec)
自然语言是我们用来表达意义的复杂系统。在这个体系中,词是语言意义的基本单位。顾名思义,词向量是用来表示一个单词的向量。它也可以被认为是一个单词的特征向量。将词映射到实数向量的技术也称为词嵌入。近年来,词嵌入逐渐成为自然语言处理的基础知识。
Why Not Use One-hot Vectors?
在第8.5节中,我们使用了一个独热向量来表示单词(字符就是单词)。回想一下,当我们假设在词典中不同的单词的数量(词典大小)是 $N$, 每个单词可以一对一的从整数0连续对应到整数 $N - 1$。 这些与单词对应的整数称为单词的索引。我们假设一个词的索引是 $i$, 为了得到单词的一个热向量表示,我们创建一个长度为 $N$ 的全0的向量并将元素 $i$ 置为 1。通过这种方式, 每个词可以表示为长度为 $N$ 的向量, 它可以直接用于神经网络。
虽然一个独热词向量很容易构建,但它们通常不是一个好的选择。其中一个主要原因是独热的词向量不能准确表达不同词之间的相似度,例如我们常用的余弦相似度。对于向量 $x, y \in R^d$, 它们的余弦相似度是它们夹角的余弦:
\[\frac{x^T y}{\| x \| \| y \|} \in [-1, 1]\]由于任意两个不同单词的一个独热向量之间的余弦相似度为0,因此很难用一个独热向量来准确地表示多个不同单词之间的相似度。
Word2vec是我们用来解决上述问题的一个工具。它用一个固定长度的向量表示每个单词,并使用这些向量更好地表示不同单词之间的相似和相似关系。Word2Vec工具包含两个模型: skip-gram Mikolov et al., 2013b 和 continuous bag of words (CBOW) Mikolov et al., 2013a。 下面我们来看看这两种模型及其训练方法。
The Skip-Gram Model
skip-gram模型假设可以使用一个单词来生成文本序列中包围它的单词。例如,我们假设文本序列是“the”, “man”, “loves”, “his”, 和 “son”. 我们使用 “loves” 作为中心目标词 并且 设置文本窗口大小为2。 如图所示, 在给定中心目标词 love 的情况下,skip-gram模型考虑生成上下文词的条件概率, “the”, “man”, “his” 和 “son”, 它们距离中心词的距离不超过2个单词:
\[P(the, man, his, son \mid loves)\]我们假设,给定中心目标词,上下文词是相互独立生成的。在这种情况下,上面的公式可以改写为
\[P(the \mid loves) · P(man \mid loves) · P(his \mid loves) · P(son \mid loves)\]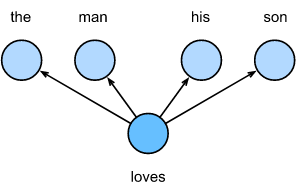
在skip-gram模型中,每个词表示为两个d维向量,用于计算条件概率。我们假设这个词在词典中的索引是 $i$, 当它为中心词时, 向量被表示为 $v_i \in R^d$, 当它为上下文词时, 向量被表示为 $u_i \in R^d$。 令中心目标词 $w_c$ 和 上下文词 $w_o$ 在词典中的索引分别为 $c$ 和 $o$。 通过对向量内积执行softmax操作,可以获得给定中心目标词生成上下文词的条件概率:
\[P(w_o \mid w_c) = \frac{exp(u_0^T v_c)}{\sum_{i \in V} exp(u_i^T v_c)}\]其中词的索引集合为 $V = {0, 1, …, \mid V \mid - 1}$。 假设给定序列长度为 $T$ 的文本, 其中每个时间 $t$ 的词表示为 $w^{t}$。 假设上下文词是根据中心词独立生成的。当上下文窗口大小为$m$, skip-gram模型的似然函数是 给定任意中心词 生成的所有上下文词的联合概率。
\[\prod_{i=1}^T \prod_{-m \leq j \leq m, j \neq 0} P(w^{(t + j)} \mid w^{(t)})\]这里, 任意小于 $1$ 或者大于 $T$ 的时间步可以忽略。
Q: 为什么最大似然估计用的是乘法?
A: 多个独立事件同时发生的概率公式
Skip-Gram Model Training
skip-gram模型参数是每个单词的中心目标词向量和上下文词向量。在训练过程中,我们将通过最大化似然函数来学习模型参数,也称为最大似然估计。它等价于使下面的损失函数最小化:
\[- \sum_{t=1}^T \sum_{-m \leq j \leq m, j \neq 0} log P(w^{(t+j)} \mid w^{(t)})\]如果我们使用SGD,在每次迭代中,我们都要通过随机抽样选择一个较短的子序列来计算该子序列的损失,然后计算梯度来更新模型参数。梯度计算的关键是计算中心词向量和上下文词向量的对数条件概率的梯度。根据定义,我们首先有:
\[log P(w_0 \mid w_c) = u_o^T v_c - log (\sum_{i \in V} exp(u_i^T v_c))\]通过求导, 我们可以从以上公式的到梯度 $v_c$.
\[\begin{aligned} \frac{\partial log P(w_o \mid w_c)}{\partial v_c} &= u_o - \frac{\sum_{j \in V}exp(u_j^T v_c)u_j}{\sum_{i \in V}exp(u_i^T v_c)} \\ &= u_o - \sum_{j \in V} \left(\frac{exp(u_j^T v_c)}{\sum_{i \in V} exp(u_i^T v_c)}\right) \\ &= u_o - \sum_{j \in V} P(w_j \mid w_c) u_j \end{aligned}\]给定中心目标词 $w_c$ , 它的计算得到在词典中的所有词的条件概率. 然后,我们使用同样的方法来获得其他词向量的梯度。
在训练之后,对于任意在词典中索引为 $i$ 的单词, 我们将要得到它的两个词向量集 $v_i$ 和 $u_i$。 在自然语言处理的应用中, 在skip-gram模型中的中心词向量经常被用来作为一个词的表征向量。
The Continuous Bag of Words (CBOW) Model
continuous bag of words (CBOW) 模型 和 skip-gram 模型相似。 最大的区别是CBOW模型假设中心目标词是根据文本序列中前后的上下文词生成的。在相同的文本序列 “the”, “man”, “loves”, “his” 和 “son” 中, “love” 是中心目标词, 给定上下文窗口大小为2, CBOW模型关心 基于上下文词 “the”, “man”, “his” 和 “son” (如图所示)生成目标词 “love” 的条件概率。
\[P(love \mid the, man, his, son)\]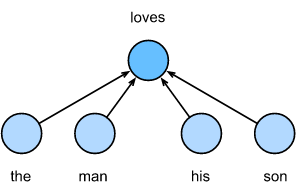
由于CBOW模型中有多个上下文词,我们将其词向量平均,然后使用与skip-gram模型相同的方法来计算条件概率。我们假设 $v_i \in R^{d}$ 并且 $u_i \in R^{d}$ 是在词典中索引为 $i$ 的上下文词向量 和 中心目标词向量(注意: 这些符号和skip-gram模型中的符号相反)。令中心目标词$w_c$的索引为$c$, 上下文词$w_{o_1}, …, w_{o_{2m}}$的索引为 $o_1, …, o_{2m}$。 由于CBOW模型中有多个上下文词,我们将其词向量平均,然后使用与skip-gram模型相同的方法来计算条件概率:
\[P(w_c \mid w_{o_1}, ..., w_{o_{2m}}) = \frac{exp(\frac{1}{2m} u_c^T (v_{o_1} + ..., + v_{o_{2m}}))}{\sum_{i \in V} exp(\frac{1}{2m}u_i^T(v_{o_1} + , ..., + v_{o_{2m}}))}\]为了简洁, 表示为 $W_o = {w_{o_1}, …, w_{o_{2m}}}$, $\bar v_0 = (v_{o_1} + …, + v_{o_{2m}}) / (2m)$。 上面的等式可以简化为:
\[P(w_c \mid W_o) = \frac{exp(u_c^T \bar v_o)}{\sum_{i \in V}exp(u_i^T \bar v_o)}\]给定长度为 $T$ 的文本序列, 我们假设在时间步 $t$ 的词是 $w^{(t)}$, 并且 上下文窗口大小为 $m$。 CBOW模型的似然函数是从上下文词生成任意中心目标词的概率。
\[\prod_{t=1}^T P(w^{(t)} \mid w^{(t-m)}, ..., w^{(t-1)}, w^{(t+1)}, ..., w^{(t+m)})\]CBOW Model Training
CBOW模型训练与skip-gram模型训练非常相似。CBOW模型的最大似然估计等价于损失函数的最小化。
\[-\sum_{t=1}^T log P(w^{(t)} \mid w^{(t-m)}, ..., w^{(t-1)}, w^{(t+1)}, ..., w^{(t+m)})\]注意到:
\[log P(w_c \mid W_o) = u_c^T \bar v_o - log\left( \sum_{i \in V}exp(u_i^T \bar v_o) \right)\]通过求导, 我们可以计算上面公式中任意上下文词向量 $v_{o_i}(i = 1, …, 2m)$ 梯度的条件概率的对数
\[\frac{\partial log P(w_c \mid W_o)}{\partial v_{o_i}} = \frac{1}{2m} \left(u_c - \sum_{j \in V} \frac{exp(u_j^T \bar v_o)u_j}{\sum_{i \in V} exp(u_i^T \bar v_o)}\right) = \frac{1}{2m} \left( u_c - \sum_{j \in V} P(w_j \mid W_o)u_j\right)\]然后,我们使用同样的方法来获得其他词向量的梯度。与skip-gram模型不同,我们通常使用上下文词向量作为CBOW模型中单词的表示向量。
Summary
- 词向量是用来表示一个词的向量。将词映射到实数向量的技术也称为词嵌入。
- Word2vec 包括 continuous bag of words (CBOW) 和 skip-gram 模型。 skip-gram模型假设上下文词基于中心目标词生成。CBOW模型假设中心目标词基于上下文词生成。
Exercises
- 每个梯度的计算复杂度是多少?如果词典里有大量的单词,这会引起什么问题呢?
- 英语中有一些固定短语是由多个单词组成的,比如new york。如何训练它们的词向量?提示:请参阅Word2vec论文的第四部分 Mikolov et al., 2013b
- 以skip-gram模型为例,考虑一下word2vec模型的设计。在skip-gram模型中,两个词向量的内积与余弦相似度之间的关系是什么?对于语义相近的一对词,为什么它们的词向量余弦相似度可能很高?