回顾上一节的内容。skip-gram模型的核心特征是使用softmax操作来计算 给定中心目标词 $w_c$, 生成上下文词$w_o$的条件概率。
\[P(w_o \mid w_c) = \frac{exp(u_p^T v_c)}{\sum_{i \in V} exp(u^T_i v_c)}\]条件概率对应的对数损失为
\[- log P(w_o \mid w_c) = - u_o^T v_c + log (\sum_{i \in V} exp(u_i^T v_c))\]因为softmax操作已经考虑到上下文单词可以是词典 $V$ 中的任何单词, 上面提到的损失实际上包括了词典中每个词的和。从上一节我们知道,对于skip-gram模型和CBOW模型,因为它们都使用softmax操作获得条件概率,所以每个步骤的梯度计算都包含字典中每个词的和。对于拥有数十万甚至数百万单词的较大字典,计算每个梯度的开销可能太高。为了减少这样的计算复杂度,我们将在本节中介绍两种近似训练方法:负采样和层次化softmax。由于skip-gram模型和CBOW模型之间没有太大的区别,所以我们在本节中只以skip-gram模型为例介绍这两种训练方法。
Negative Sampling
负采样修改了原始的目标函数。给中心目标词 $w_c$ 一个上下文窗口, 我们把它看做上下文词 $w_o$ 出现在上下文窗口的事件, 该事件发生的概率计算方法如下:
\[P(D = 1 \mid w_c, w_o) = \sigma(u_o^T v_c)\]这里, $\sigma$函数和sigmoid激活函数有着相同的定义:
\[\sigma(x) = \frac{1}{1 + exp(-x)}\]我们将首先考虑通过最大化文本序列中所有事件的联合概率来训练词向量。给定长度 $T$ 的文本序列, 我们假设在时间步 $t$ 的单词为 $w^{(t)}$, 并且窗口大小为 $m$。 现在我们考虑最大化联合概率
\[\prod_{t=1}^T \prod_{-m \leq j \leq m, j \neq 0} P(D = 1 \mid w^{(t)}, w^{(t + j)})\]然而,模型中包含的事件只考虑正面的例子。在这种情况下,只有当所有词向量都相等且值趋近于无穷时,上述联合概率才能最大化为1。显然,这样的词向量是没有意义的。负采样通过对目标函数进行正采样和负抽样,使目标函数更有意义。假设 当上下文词 $w_o$ 出现在 中心目标词 $w_c$ 的上下文窗口时, 事件 $P$ 发生, 并且我们根据分布 $P(W)$ 采样 $K$ 个没有出现在上下文的词, 将其视作噪声词。我们假设噪声词 $w_k(k=1, …, K)$ 不出现在中心目标词 $w_c$的上下文窗口的事件为 $N_k$。 假设事件 $P$ 和 $N_1, …, N_k$ 对于正样本和负样本是相互独立的。通过负采样, 我们可以重写上述 只考虑了正样本 的联合概率
\[\prod_{t=1}^T \prod_{-m \leq j \leq m, j \neq 0} P(w^{(t + j)} \mid w^{(t)})\]这里, 条件概率被估计为:
\[P(w^{(t+j)} \mid w^{(t)}) = P(D = 1 \mid w^{(t)}, w^{(t + j)}) \prod_{k=1. w_k \thicksim P(w)}^K P(D = 0 \mid w^{(t)}, w_k)\]令在时间步 $t$ 词 $w^{(t)}$ 在文本序列的索引为 $i_t$, $h_k$ 是噪声词在词典中的索引。上述条件概率的对数损失为
\[\begin{aligned} - log P(w^{t + j} \mid w^{(t)}) &= - log P(D = 1 \mid w^{(t)}, w^{(t+j)}) - \sum_{k=1, w_k \thicksim P(w)}^K log P(D = 0 \mid w^{(t)}, w_k) \\ &= - log \sigma(u_{i_{t+j}}^T v_{i_t}) - \sum_{k = 1, w_l \thicksim P(w)}^K log (1 - \sigma(u_{h_k}^T v_{i_t})) \\ &= - log \sigma(u_{i_{t+j}}^T v_{i_t}) - \sum_{k = 1, w_k \thicksim P(w)}^K log \sigma(-u_{h_k}^T v_{i_t}) \end{aligned}\]这里, 训练每一步梯度计算不再和字典大小相关, 但是和 $K$ 相关。 当 $K$ 是一个非常小的常数时, 负采样每一步的计算开销较低。
Hierarchical Softmax
层次化softmax是另一种近似训练方法。它使用如图所示的二叉树作为数据结构,树的叶子节点表示字典 $V$ 中的每个单词。
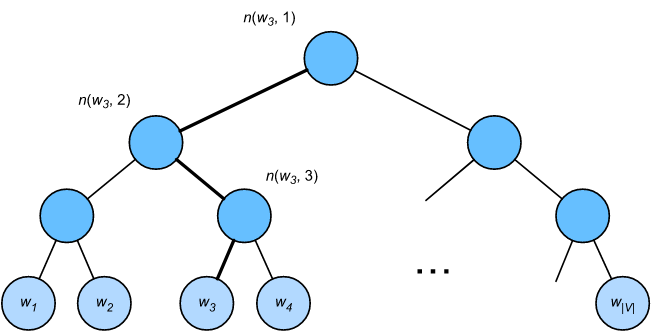
我们假设 $L(w)$ 是从二叉树的根节点到词 $w$ 的叶子节点路径上节点的数量(包括根节点和叶子节点)。 上下文词向量为$u_{n(w, j)}$, $n(w, j)$ 表示 路径上的第 $j$ 个节点。以上图为例, $L(w_3) = 4$。 在skip-gram模型中, 层次化softmax估计条件概率如下:
\[P(w_o \mid w_c) = \prod_{j=1}^{L(w_o) - 1} \sigma([[n(w_o, j+1) = leftChild(n(w_o, j))]] · u^T_{n(w_o, j)} v_c)\]这里 $\sigma$ 函数 和 sigmoid激活函数 定义相同, $leftChild(n)$ 是节点 $n$ 的左孩子节点。 如果 $x$ 为 true, [[x]] = 1; 否则 [[x]] = -1。现在, 我们计算基于上图中的词 $w_c$ 生成词 $w_3$ 的条件概率密度。 我们需要计算从根节点到 $w_3$ 路径上每个非叶子节点向量 和 词向量 $v_c$ (词$w_c$)的内积。 在二叉树中, 因为从根节点到叶子节点 $w_3$ 需要遍历 左, 右, 左 (如上图所示的粗线路径), 我们得到:
\[P(w_3 \mid w_c) = \sigma(u_{n(w_3, 1)}^T, v_c) · \sigma(- u_{n(w_3, 2)}^T v_c) · \sigma(u_{n(w_3, 3)}^T · v_c)\]因为 $\sigma(x) + \sigma(-x) = 1$, 基于给定中心目标词 $w_c$ 生成在词典 $V$ 中任意词的条件概率之和为1:
\[\sum_{w \in V} P(w \mid w_c) = 1\]此外, 因为 $L(w_o) - 1$的规模是 $O(log_2 \mid V \mid)$, 当词典大小 $V$很大时, 与不使用近似训练的情况相比,层次化softmax训练中每一步的计算开销大大减少。
Summary
- 负采样通过考虑包含正负两个采样的独立事件来构造损失函数。训练过程中每一步的梯度计算开销与我们采样的噪声单词数量线性相关。
- 层次化softmax使用二叉树,根据从根节点到叶节点的路径构造损失函数。训练过程中每一步的梯度计算开销与词典大小的对数有关。
Exercises
- 在阅读下一节之前,考虑一下我们应该如何在负采样中采样噪声词。
- 是什么让这部分的最后一个公式成立?
- 我们怎样在skip-gram模型中使用负采样和层次化softmax?