首先,我们应该回顾一下word2vec中的skip-gram模型。条件概率 $P(w_j \mid w_i)$ 在 skip_gram 模型中 使用 softmax 操作的表示 将会记录为 $q_{ij}$:
\[q_{ij} = \frac{exp(u_j^T v_i)}{\sum_{k \in V} exp(u_k^T v_i)}\]其中 $v_i$ 和 $u_i$ 分别是词 索引为 $i$ 的中心词 $w_i$ 和 上下文词 的向量表示, 并且 $V = {0, 1, …, \mid V \mid - 1}$是词典的索引集合。
对于词$w_i$, 它可能在数据集中出现多次。我们收集 当 $w_i$ 为中心词时 的 所有上下文词, 表示为 multiset $C_i$。 在一个multiset中,一个元素出现的数目称为该元素的multiplicity。比如, 假设词 $w_i$ 在数据集中出现两次: 当这两个 $w_i$ 变成中心词时, 上下文窗口包含上下文词的索引为 2, 1, 5, 2 和 2, 3, 2 , 1。那么, numtiset $C_i = {1, 1, 2, 2, 2, 2, 3, 5}$, 其中元素 1 的 multiplicity 为 2, 元素 2 的 multiplicity 为 4, 元素 3 和 元素 5 的multiplicity都为1。 将 multiset $C_i$ 中的 元素$j$ 的multiplicity 表示为 $x_{ij}$: 表示在整个数据集里 对于 中心词 $w_i$ 的 所有上下文词, 词 $w_j$ 的数量。 最后, skip-gram 模型的损失函数可以被表示为一种不同的方式:
\[- \sum_{i \in V} \sum_{j \in V} x_{ij} \log q_{ij}\]Note: 原始的损失函数:
\[-\sum_{t=1}^T \sum_{-m \leq j \leq m, j \neq 0} \log P(w^{(t + j)} \mid w^{(t)})\]我们把中心目标词 $w_i$ 的所有上下文词的数量加起来 得到 $x_i$, 并且 将基于中心目标词 $w_i$ 生成上下文词 $w_j$ 的 条件概率 $x_{ij} / x_i$ 记录 为 $p_{ij}$。 我们可以重写 skip-gram 模型的损失函数为:
\[- \sum_{i \in V} x_i \sum_{j \in V} p_{ij} \log q_{ij}\]在上面的公式中, $\sum_{j \in V} p_{ij} \log q_{ij}$ 计算基于中心目标词 $𝑤_𝑖$的上下文词生成的条件概率分布 $p_{ij}$ 和 由模型预测的条件概率分布 $q_{ij}$ 的交叉熵。损失函数 使用中心目标词 $w_i$ 的上下文词的数量和 进行加权。 如果我们最小化上面公式中的损失函数,我们就能够让预测的条件概率分布尽可能接近真实的条件概率分布。
然而,交叉熵损失函数尽管是最常见的损失函数类型,但它有时不是一个好的选择。一方面, 让模型预测 $q_{ij}$ 变成合理的概率分布的代价是需要让它的分母是整个词典的所有项之和。另一方面,词典中往往有很多不常见的词,它们在数据集中很少出现, 在交叉熵损失函数中,对大量很少出现的词的条件概率分布的最终预测很可能是不准确的。
The GloVe Model
为了解决这个问题,word2vec之后的词嵌入模型GloVe [Pennington et al., 2014]采用了平方损失,并在此损失的基础上对skip-gram模型进行了三处修改。
- 这里, 我们使用非概率分布变量 $p_{ij}’ = x_{ij}$ 以及 $q_{ij}’ = exp(u_j^T v_i)$ 并 取它们的对数。因此, 我们得到平方损失 $(\log p_{ij}’ - \log q_{ij}’)^2 = (u_j^T v_i - \log x_{ij})^2$
- 我们为每个词 $w_i$ 增加了两个标量: bias项 $b_i$ (对中心目标词) 和 $c_i$ (对上下文词)。
- 用函数 $h(x_{ij})$ 替代每个 loss的权重。 权重函数 $h(x)$ 是一个区间为 $[0, 1]$ 的单调递增函数。
因此, GloVe的目标是最小化损失函数:
\[\sum_{i \in V} \sum_{j \in V} h(x_{ij}) (u_j^T v_i + b_i + c_j - \log x_{ij})^2\]这里, 我们有一个权重函数 $h(x)$ 选择的建议: 当 $x < c (\text{e.g c = 100})$,使得 $h(x) = (x / c)^\alpha (\text{e.g } \alpha = 0.75)$, 否则使 $h(x) = 1$。 因为 $h(0) = 0$, 平方损失项对于 $x_{ij} = 0$ 可以简单地忽略。 当我们使用 minibatch SGD 训练时, 我们使用 随机采样以 使得 从每个时间步 得到一个非零的 minibatch $x_{ij}$, 然后计算梯度并更新模型参数。 这些非0 $x_{ij}$ 基于整个数据集预先计算 并且 它们 包含数据集的全局数据。 因此, GloVe的名字来自于 “Global Vectors”。
注意到如果词 $w_i$ 出现在 词 $w_j$ 的上下文窗口中, 词 $w_j$ 将会也出现在 $w_i$ 的上下文窗口中。 因此 $x_{ij} = x_{ji}$。 不像 word2vec, GloVe 使用对称 $\log x_{ij}$ 代替非对称条件概率 $p_{ij}$。 因此, 任意词的中心目标词向量和上下文词向量在GloVe中是等价的。 然而, 由于初始化的不同,同一词学习到的两组词向量最终可能不同。 在学习完所有的词向量后,GloVe将中心目标词向量和上下文词向量的总和作为该词的最终词向量。
Understanding GloVe from Conditional Probability Ratios
我们也可以从另一个角度尝试理解 GloVe 词嵌入。我们将会继续沿用前面部分的符号, $P(w_j \mid w_i)$ 表示在数据集中 中心目标词 $w_i$ 生成 上下文词 $w_j$ 的条件概率, 并且它被记录为 $p_{ij}$。这里是来自语料库的一个真实样本, 我们有以下两组条件概率,以ice和steam为中心目标词以及它们之间的比率:
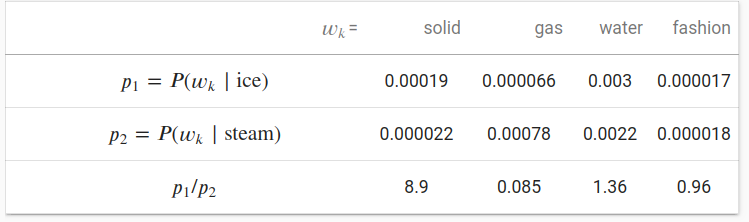
我们可以观察到如下现象:
- 对于一个词 $w_k$, 它和 “ice” 相关 而 不和 “steam” 相关,比如 $w_k=$ solid, 我们希望得到一个更大的条件概率比,比如上面表格最后一行中的值8.9。
- 对于一个词 $w_k$, 它和 “steam” 相关 而 不和 “ice” 相关, 比如 $w_k=$ gas, 我们期望一个更小的条件概率比,就像上面表格最后一行中的值0.085。
- 对于一个词 $w_k$, 它与 “steam” 和 “ice” 都相关, 比如 $w_k=$ water,我们期望条件概率比接近1,就像上面表格最后一行中的值1.36。
- 对于一个词 $w_k$, 它与 “steam” 和 “ice” 都不相关, 比如 $w_k=$ fashion ,我们期望条件概率比接近1,就像上面表格最后一行中的值0.96。
可以看出,条件概率比可以更直观地表示不同单词之间的关系。我们可以构造一个词向量函数来更有效地拟合条件概率比。我们知道,要得到这种类型的比率,需要三个单词$w_i, w_j$ 和 $w_k$。 以$𝑤_𝑖$为中心目标词的条件概率比为$𝑝_{𝑖𝑗}/𝑝_{𝑖𝑘}$。我们可以找到一个使用词向量的函数来拟合这个条件概率比。
\[f(u_j, u_k. v_i) \approx \frac{p_{ij}}{p_{ik}}\]函数 $f$ 设计的可能性不是唯一的。 我们只需考虑一种更合理的可能性。注意到条件概率比是一个标量, 我们可以限制 $f$ 为一个标量函数: $f(u_j, u_k, v_i) = f((u_j - u_k)^T v_i)$。 在交换 $j$ 和 $k$的索引后, 我们可以看到函数 $f$ 满足条件 $f(x)f(-x) = 1$, 因此一个可能的函数为 $f(x) = exp(x)$, 因此:
\[f(u_j, u_k, v_i) = \frac{exp(u_j^T v_i)}{exp(u_k^T v_i)} \approx \frac{p_{ij}}{p_{ik}}\]满足近似号右边的一种可能性是 $\exp(u_j^T v_i) \approx \alpha p_{ij}$, 其中 $\alpha$ 是一个常数。 考虑到 $p_{ij} = x_{ij} / x_i$, 在取对数后我们得到 $u_j^T v_i \approx \log \alpha + \log x_{ij} - \log x_i$。 我们使用额外的bias项拟合 $-\log \alpha + \log x_i$, 例如中心目标词bias项 $b_i$ 和 上下文词 bias 项 $c_j$:
\[u_j^T v_i + b_i + c_j \approx \log(x_{ij})\]对上述公式的左右两边进行平方误差 以及 加权,可以得到 GloVe 的损失函数。
Summary
- 某些情况下,交叉熵损失函数可能有缺点。GloVe使用平方损失和词向量来拟合基于整个数据集预先计算的全局统计数据。
- 所有单词的中心目标词向量和上下文词向量都是等价的。
Exercises
- 如果一个单词出现在另一个单词的上下文窗口中,我们如何利用它们在文本序列中的距离来重新设计计算条件概率 $p_{ij}$ 的方法? 提示: 参见Glove论文的4.2节 [Pennington et al., 2014]。
- 对于任何一个词来说,它的中心目标词和上下文词的bias项是否完全等价?为什么?