在实践中,给定相同的一组 queries、keys和values,我们可能希望我们的模型结合来自同一注意力机制的不同行为的知识,例如捕获序列中不同范围的依赖关系(例如,较短范围和较长范围)。因此,允许我们的注意力机制联合使用queries、keys 和 values 的不同表示子空间可能是有益的。
为此,queries、keys和values可以通过 $h$ 独立学习的线性投影进行转换,而不是执行单个注意力池化。然后这些 $h$ 投影的queries、keys 和 values 被并行地输入到注意力池化中。最后,$h$ 注意力池化输出进行concatenate 与 另一个学习到的线性投影和转换,产生最终的输出。这种设计叫做 multi-head attention,其中每个 $h$ 注意力池化输出是一个 head [Vaswani et al., 2017] 。使用全连接层实现可学习的线性变换, 图10.5.1描述了 multi-head attention。
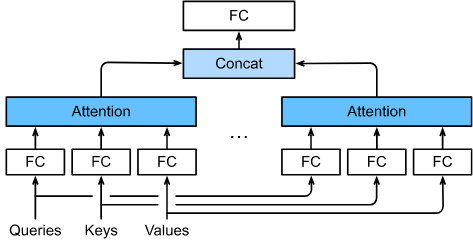
图10.5.1 Multi-head attention, 其中多个 head 被 concatenate 起来, 然后进行线性变换。
Model
在实现 multi-head attention 之前, 让我们用数学方法将这个模型公式化。 给定 query $Q \in \mathbb{R}^{d_q}$, 一个 key $k \in \mathbb{R}^{d_k}$ 和一个 value $v \in \mathbb{R}^{d_v}$, 每个attention head $h_i(i=1, …, h)$可以计算如下:
\[h_i = f(W_i^{(q)}q, W_i^{(k)}k, W_i^{(v)}v) \in R^{p_v} \tag{10.5.1}\]其中可学习参数 $W_i^{(q)} \in \mathbb{R}^{p_q \times d_q}$, $W_i^{(k)} \in \mathbb{R}^{p_k \times d_k}$, 和 $W_i^{(v)} \in \mathbb{R}^{p_v \times d_v}$, $f$是注意力池化, 比如10.3节中的 additive attention 和 scaled dot-product attention。multi-head attention 输出 是 另一个线性变换, 通过 $h$ heads 的拼接的 可学习参数 $W_o \in \mathbb{R^{p_o \times hp_v}}$:
\[W_o \begin{matrix} \left[\begin{array}{cc} h_1 \\ \vdots \\ h_h \end{array}\right] \end{matrix} \in \mathbb{R}^{p_o} \tag{10.5.2}\]基于这个设计, 每个 head 可以处理输入的不同部分。 可以表达比简单加权平均更复杂的函数。
1
2
3
4
import math
import torch
from torch import nn
from d2l import torch as d2l
Implementation
在我们的实现中,我们为multi-head attention的每个 head 选择 scaled dot-product attention。避免了计算代价和参数代价的显著增长, 我们令 $p_q = p_k = p_v = p_o / h$。 注意 $h$ heads 可以并行计算 如果我们将query、key和value的线性变换的输出数量设置为 $p_qh = p_kh = p_vh = p_o$。 在接下来的实现中, $p_o$ 通过参数 num_hiddens 决定。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
class MultiHeadAttention(nn.Module):
def __init__(self, key_size, query_size, value_size, num_hiddens,
num_heads, dropout, bias=False, **kwargs):
super(MultiHeadAttention, self).__init__(**kwargs)
self.num_heads = num_heads
self.attention = d2l.DotProductAttention(dropout)
self.W_q = nn.Linear(query_size, num_hiddens, bias=bias)
self.W_k = nn.Linear(key_size, num_hiddens, bias=bias)
self.W_v = nn.Linear(value_size, num_hiddens, bias=bias)
self.W_o = nn.Linear(num_hiddens, num_hiddens, bias=bias)
def forward(self, queries, keys, values, valid_lens):
"""
args:
queries : shape(2, 4, 100)
keys : shape(2, 6, 100)
values : shape(2, 6, 100)
valid_lens : torch.tensor([3, 2])
return:
output_concat : shape(2, 4, 100)
"""
# Shape of `queries`, `keys`, or `values`:
# (`batch_size`, no. of queries or key-value pairs, `num_hiddens`)
# Shape of `valid_lens`:
# (`batch_size`,) or (`batch_size`, no. of queries)
# After transposing, shape of output `queries`, `keys`, or `values`:
# (`batch_size` * `num_heads`, no. of queries or key-value pairs, `num_hiddens` / `num_heads`)
# queries.shape: (2, 4, 100) -> (2*5, 4, 20)
queries = transpose_qkv(self.W_q(queries), self.num_heads)
# keys.shape: (2, 6, 100) -> (2*5, 6, 20)
keys = transpose_qkv(self.W_k(keys), self.num_heads)
# values.shape: (2, 6, 100) -> (2*5, 6, 20)
values = transpose_qkv(self.W_v(values), self.num_heads)
if valid_lens is not None:
# On axis 0, copy the first item (scalar or vector) for
# `num_heads` times, then copy the next item, and so on
# [3, 2] -> [3, 3, 3, 3, 3, 2, 2, 2, 2, 2]
valid_lens = torch.repeat_interleave(valid_lens,
repeats=self.num_heads,
dim=0)
# Shape of `output`: (`batch_size` * `num_heads`, no. of queries, `num_hiddens` / `num_heads`)
# queries.shape: (10, 4, 20)
# keys.shape: (10, 6, 20)
# values.shape: (10, 6, 20)
# output: (10, 4, 20)
output = self.attention(queries, keys, values, valid_lens)
# Shape of `output_concat`:
# (`batch_size`, no. of queries, `num_hiddens`)
output_concat = transpose_output(output, self.num_heads)
return self.W_o(output_concat)
为了实现 multiple head 的并行计算, 上述 MultiHeadAttention 类使用如下定义的两个转置函数。 transpose_output 函数 是 transpose_qkv 函数的逆操作。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
def transpose_qkv(X, num_heads):
"""
args:
X : shape (2, 4, 100)
num_heads: 5
return:
X : shape (2 * 5, 4, 20)
"""
# Shape of input `X`: (`batch_size`, no. of queries or key-value pairs, `num_hiddens`).
# Shape of output `X`: (`batch_size`, no. of queries or key-value pairs, `num_heads`, `num_hiddens` / `num_heads`)
# X.shape: (2, 4, 100) -> (2, 4, 5, 20)
X = X.reshape(X.shape[0], X.shape[1], num_heads, -1)
# Shape of output `X`:
# (`batch_size`, `num_heads`, no. of queries or key-value pairs, `num_hiddens` / `num_heads`)
X = X.permute(0, 2, 1, 3)
# Shape of `output`:
# (`batch_size` * `num_heads`, no. of queries or key-value pairs, `num_hiddens` / `num_heads`)
return X.reshape(-1, X.shape[2], X.shape[3])
def transpose_output(X, num_heads):
"""
args:
X : shape(10, 4, 20)
num_heads : 5
return:
X : shape(2, 4, 100)
"""
"""Reverse the operation of `transpose_qkv`"""
# X.shape: (10 ,4, 20) -> (2, 5, 4, 20)
X = X.reshape(-1, num_heads, X.shape[1], X.shape[2])
# X.shape: (2, 5, 4, 20) -> (2, 4, 5, 20)
X = X.permute(0, 2, 1, 3)
# X.shape: (2, 4, 5, 20) -> (2, 4, 100)
return X.reshape(X.shape[0], X.shape[1], -1)
让我们使用一个keys 和 values 都相同的简单样本实现 MultiHeadAttention。 multi-head attention 的输出的形状是 (batch_size, num_queries, num_hiddens)。
1
2
3
4
num_hiddens, num_heads = 100, 5
attention = MultiHeadAttention(num_hiddens, num_hiddens, num_hiddens,
num_hiddens, num_heads, 0.5)
attention.eval()
输出:
1
2
3
4
5
6
7
8
9
MultiHeadAttention(
(attention): DotProductAttention(
(dropout): Dropout(p=0.5, inplace=False)
)
(W_q): Linear(in_features=100, out_features=100, bias=False)
(W_k): Linear(in_features=100, out_features=100, bias=False)
(W_v): Linear(in_features=100, out_features=100, bias=False)
(W_o): Linear(in_features=100, out_features=100, bias=False)
)
1
2
3
4
5
batch_size, num_queries, num_kvpairs, valid_lens = 2, 4, 6, torch.tensor([
3, 2])
X = torch.ones((batch_size, num_queries, num_hiddens))
Y = torch.ones((batch_size, num_kvpairs, num_hiddens))
attention(X, Y, Y, valid_lens).shape
输出
1
torch.Size([2, 4, 100])
Summary
- Multi-head attention 通过queries, keys和values的子空间的不同表征 组合了 相同注意力池化 的知识。
- 为了并行计算 multi-head attention 的 multiple heads, 需要合适的 tensor 操作。
Exercises
- 可视化实验中 multiple heads 的 注意力权重。
- 假设我们有一个基于multi-head attention的训练模型,我们想要修剪最不重要的attention head 来提高预测速度。我们如何设计实验来衡量attention head的重要性呢?