凸性在优化算法设计中起着至关重要的作用。这主要是因为在这样的环境中分析和测试算法要容易得多。换句话说，如果算法即使在凸性设置下也表现不佳，那么我们通常就不应该期望在其他情况下看到很好的结果。此外，尽管深度学习中的优化问题一般是非凸的，但它们往往在局部极小点附近表现出凸的一些性质。

%matplotlib inline
import numpy as np
import torch
from mpl_toolkits import mplot3d
from d2l import torch as d2l

Definitions

在进行凸分析之前，我们需要定义凸集和凸函数。它们导致了通常用于机器学习的数学工具。

Convex Sets

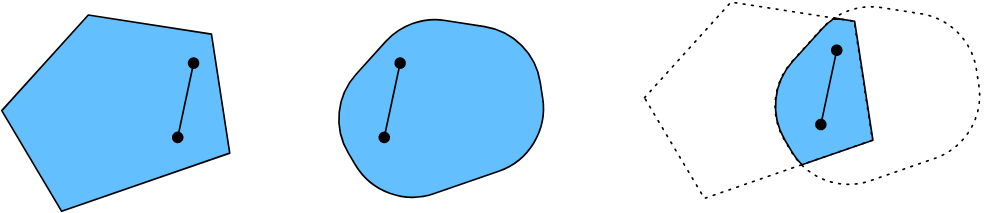
集合是凸性的基础。简单地说，向量空间中的集合 $\mathcal{X}$ 如果对于任意的 $a, b \in \mathcal{X}$， $a$ 和 $b$ 的连线也在 $\mathcal{X}$ 中，那么这个集合就是凸的。

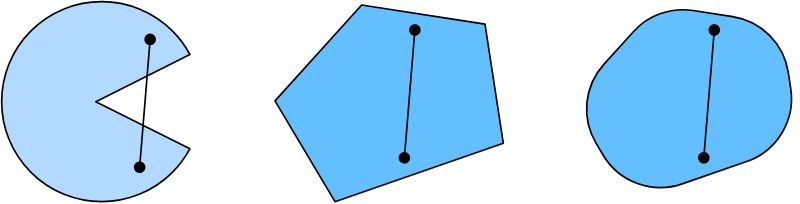
定义本身并不是特别有用，除非你能对它们做些什么。假设 $\mathcal{X}$ 和 $\mathcal{Y}$ 是凸集。那么 $\mathcal{X} \cap \mathcal{Y}$ 也是凸集。

我们可以用一些努力来加强这个结果：给定凸集 $\mathcal{X_i}$，它们的并集 $\cap_i \mathcal{X}_i$是凸的。注意，这个的逆命题是不成立的，假设两个不相交的集合 $\mathcal{X} \cap \mathcal{Y} = \varnothing$。现在选择 $a \in \mathcal{X}$ 并且 $b \in \mathcal{Y}$。 $a$ 和 $b$ 的连线的部分在 $\mathcal{X}$ 和 $\mathcal{Y}$ 的外面。

深度学习中的问题通常定义在凸集上。例如， $\mathbb{R}^d$，一个d维实数向量的集合，是一个凸集($\mathbb{R}$^d 上两个点的连线仍然在 $\mathbb{R}^d$ 上)。在某些情况下我们处理有界长度的变量，比如球的半径，定义如 ${x \mid x \in \mathbb{R}^d \text{ and } |x| \leq r}$。

Convex Functions

现在我们由凸集引入凸函数 $f$。给定一个凸集 $\mathcal{X}$, 以及 $f： \mathcal{X} \rightarrow \mathbb{R}$, 对所有 $x, x’ \in \mathcal{X}$ 以及对所有 $\lambda \in [0, 1]$有如下关系，那么函数是凸的：

\[\lambda f(x) + (1 - \lambda)f(x') \geq f(\lambda x + (1 - \lambda) x')\]

为了说明这一点，让我们绘制一些函数，并检查哪些函数满足要求。下面我们定义几个函数，包括凸函数和非凸函数。

f = lambda x: 0.5 * x**2  # Convex
g = lambda x: torch.cos(np.pi * x)  # Nonconvex
h = lambda x: torch.exp(0.5 * x)  # Convex

x, segment = torch.arange(-2, 2, 0.01), torch.tensor([-1.5, 1])
d2l.use_svg_display()
_, axes = d2l.plt.subplots(1, 3, figsize=(9, 3))
for ax, func in zip(axes, [f, g, h]):
    d2l.plot([x, segment], [func(x), func(segment)], axes=ax)

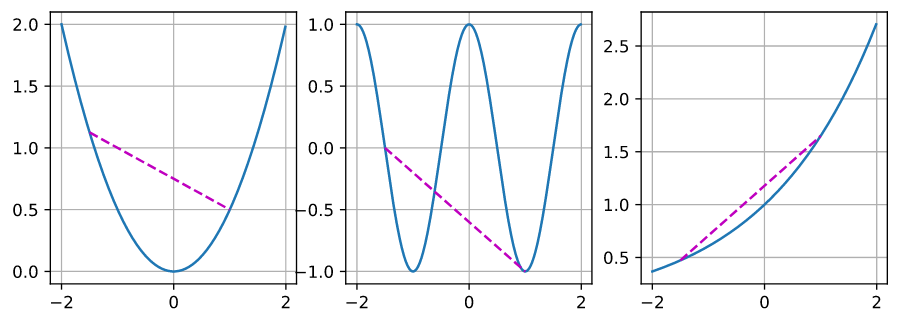
正如预期的那样，余弦函数是非凸函数，而抛物线函数和指数函数是凸函数。注意 $\mathcal{X}$ 是凸集是必要条件。否则 $f(\lambda x + (1 - \lambda)x’)$ 可能没有定义。

Jensen’s Inequality

给定一个凸函数 $f$，一个最有用的数学工具是 Jensen 不等式。这相当于对凸性定义的推广：

\[\sum_i \alpha_i f(x_i) \geq f(\sum_i \alpha_i x_i) \text{ and } E_X[f(X)] \geq f(E_X[X])\]

其中 $\alpha_i$ 是非负实数， $\sum_i \alpha_i = 1$ 并且 $X$ 是一个随机变量。换句话说，凸函数的期望不小于一个期望的凸函数，而后者通常是一个更简单的表达式。为了证明第一个不等式，我们对求和中的一项反复应用凸性的定义。

Jensen不等式的一个常见应用是用一个简单的表达式来限定一个较复杂的表达式。例如，它的应用可以是关于部分观察到的随机变量的对数似然。也就是说，我们使用

\[E_{Y \thicksim P(Y)} [- \log P(X \mid Y)] \geq - \log P(X)\]

因为 $\int P(X) P(X \mid Y)dY = P(Y)$。这可以用在变分方法中。这里 $Y$ 通常是未观测到的随机变量， $P(Y)$ 它可能的分布的最优猜测， $P(X)$ 是集成 $Y$ 后的分布。例如，聚类 $Y$ 可能是聚类标签并且 $P(X \mid Y)$ 是应用聚类标签的生成模型。

Properties

凸函数有许多有用的性质。下面我们将介绍几种常用的方法。

Local Minima Are Global Minima

首先，凸函数的局部极小值也是全局极小值。我们可以用下面的反证法来证明它。

Below Sets of Convex Functions Are Convex

我们可以通过下面的凸函数集方便地定义凸集。具体地，给定一个定义在凸集 $\mathcal{X}$ 上的凸函数 $f$, ：

\[S_b := \{x \mid x \in \mathcal{X} \text{ and } f(x) \leq b\}\]

是凸的。

Convexity and Second Derivatives

函数的二阶导数 $f: \mathbb{R}^n \rightarrow \mathbb{R}$ 是否存在一个非常容易的方式是检查函数 $f$ 是否为凸函数。我们需要去检查函数 $f$ 的海森矩阵是不是半正定的： $\nabla^2 f \geq 0$。

Constraints

凸优化的一个很好的性质是它允许我们有效地处理约束。也就是说，它允许我们解决这种形式的约束优化问题：

\[\mathop{\text{minimize}}_x f(x) \\ \mathop{\text{subject to }} c_i(x) \leq 0 \text{ for all } i \in \{1, ..., n\}\]

其中 $f$ 是目标函数， $c_i$ 是约束函数。让我们来看一个例子， $c_1(x) = |x|_2 - 1$。在这个例子下，参数 $x$ 的约束是一个单位球。如果第二个约束是 $c_2(x) = v^Tx + b$，这个约束对应的是 $x$ 在半个空间中。同时满足这两个约束等于选择一个球的切面。

Lagrangian

一般来说，求解约束优化问题是困难的。解决这个问题的一种方法来自物理学，带有相当简单的直觉。想象一个球在一个盒子里。球就会滚到最低的地方，重力就会被盒子两边施加在球上的力抵消。简而言之，目标函数(即重力)的梯度将被约束函数的梯度所抵消(由于墙的反推，球需要留在盒子内)。注意，有些约束可能不是总是存在的:没有被球接触的墙壁将不能对球施加任何力。

跳过拉格朗日的推导 $L$，以上推理可以用下面的鞍点优化问题来表示：

\[L(x, \alpha_1, ..., \alpha_n) = f(x) + \sum_{i=1}^n \alpha_i c_i(x) \qquad \text{ where } \alpha_i \geq 0\]

这里的变量 $\alpha_i(i=1, …, n)$ 叫做拉格朗日乘子确保适当地执行约束。它们的选择确保对于所有的 $i$， $c_i(x) \leq 0$。例如，对于任意的 $x$，其中 $c_i(x) < 0$, 我们最终选择 $\alpha_i = 0$。此外，这是一个鞍点优化问题，对于所有$\alpha_i$ 想要最大化 $L$，同时对于每个 $x$ 最小化 $L$. 有大量的文献解释如何达到这个功能 $L(x, \alpha_1, …, \alpha_n)$。对于我们的目的而言，直到$L$的鞍点是原始约束优化问题最优解的地方就足够了。

Penalties

近似地满足约束优化问题的一种方法是采用拉格朗日函数 $L$。与其满足 $c_i(x) \leq 0$，我们仅将 $\alpha_i c_i(x)$ 加在目标函数 $f(x)$ 的后面。这确保了约束不会被严重违反。

事实上，我们一直在使用这个技巧。如4.5节的权重衰减。我们对目标函数加上 $\frac{\lambda}{2} |w|^2$ 来确保 $w$ 不会变得过大。从约束优化的角度来看，我们可以看到这将确保 $|w|^2 - r^2 \leq 0$, 对于一些半径 $r$。调整 $\lambda$ 的值允许 $w$ 的大小变化。

通常，添加惩罚是确保近似约束满足的好方法。在实践中，这比确切的满足更有说服力。此外，对于非凸问题，使得在凸情况下如此吸引人的许多性质(例如，最优性)不再成立。

Projections

满足约束条件的另一种策略是投影。同样，我们以前也遇到过它们，例如，在8.5节中处理梯度裁剪时。我们通过以下的式子确保梯度的长度由 $\theta$ 约束：

\[g \leftarrow g · \min (1, \theta / \|g\|)\]

这表明 $g$ 的投影到一个半径为 $\theta$ 的球上。更通用地，凸集 $\mathcal{X}$ 的投影被定义为：

\[Proj_X(x) = \mathop{\text{argmin}}_{x' \in \mathcal{X}} \|x - x'\|\]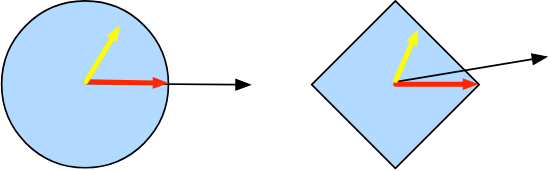

投影的数学定义可能听起来有点抽象。上图解释地可能更清楚一些。它有两个凸集，一个圆形和一个菱形。两个集合(黄色)内的点在投影期间保持不变。两个集合(黑色)之外的点被投影到集合(红色)内靠近原始点(黑色)的点。$L2$ 的球状使得方向没有发生改变，但它是一个特例，比如钻石形的情况。

凸投影的一个用途是计算稀疏权向量。在这种情况下，我们投影权重向量到 $L_1$ 球体，它比钻石形的版本更具泛化力。

Summary

在深度学习的背景下，凸函数的主要目的是启发优化算法，并帮助我们详细了解它们。下面我们将看到梯度下降和随机梯度下降是如何推导的。

凸集的交集是凸的，并集不是。
一个凸函数的期望不小于一个期望的凸函数(Jensen不等式)。
一个二次可微函数是凸的当且仅当它的Hessian(二阶导数矩阵)是正半定的。
凸约束可以通过拉格朗日来添加。在实践中，我们可以简单地将它们加上一个惩罚加到目标函数中。
投影映射到最接近原始点的凸集上的点。

【d2l】Convexity