在这一节中，我们将介绍梯度下降的基本概念。虽然它很少直接用于深度学习，但理解梯度下降是理解随机梯度下降算法的关键。例如，由于过大的学习率，优化问题可能会发散。这种现象在梯度下降中已经可以看到。同样地，预处理是梯度下降中的一种常见技术，并可用于更高级的算法。

One-Dimensional Gradient Descent

一维梯度下降就是一个很好的例子来解释为什么梯度下降算法可以降低目标函数的值。考虑一个连续可微的实值函数 $f: \mathbb{R} \rightarrow \mathbb{R}$。用泰勒展开式得到：

\[f(x + \epsilon) = f(x) + \epsilon f'(x) + O(\epsilon^2)\]

也就是说，一阶估计 $f(x + \epsilon)$ 由函数值 $f(x)$ 和在 $x$ 处的一阶导数 $f’(x)$ 得到。假设小的 $\epsilon$ 向负梯度方向移动将减小 $f$ 并非不合理。为了保持简单，我们选择固定步长大小 $\eta > 0$ 并且选择 $\epsilon = -\eta f’(x)$。将它插入泰勒展开，我们得到：

\[f(x - \eta f'(x)) = f(x) - \eta f'^2(x) + O(\eta^2 f'^2(x))\]

如果导数 $f’(x) \neq 0$ 不会消失，因为$\eta f’^2(x) > 0$, 我们将得到进展。此外，我们总可以选择足够小的 $\eta$ 使得高阶项变得无关紧要。因此我们得出：

\[f(x - \eta f'(x)) \mathop{<}_{\approx} f(x)\]

这意味着，如果我们使用

\[x \leftarrow x - \eta f'(x)\]

去迭代 $x$，函数 $f(x)$ 的值可能下降。因此，在梯度香江中我们首先选择一个初始值 $x$ 和一个常数 $\eta > 0$ 并且使用他们连续地迭代 $x$，直到停止条件达到。

为了简单，我们选择目标函数 $f(x) = x^2$ 去解释如何实现梯度下降。尽管我们知道 $x = 0$ 是最小化 $f(x)$ 的解，我们仍然使用这个简单的函数来观察 $x$ 如何变化。

%matplotlib inline
import numpy as np
import torch
from d2l import torch as d2l


def f(x):  # Objective function
    return x**2

def f_grad(x):  # Gradient (derivative) of the objective function
    return 2 * x

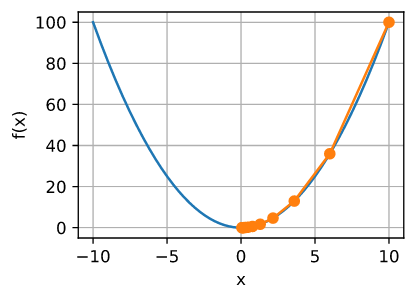
接下来，我们使用 $x = 10$ 作为初始值，并且假设 $\eta = 0.2$。使用梯度下降迭代 $x$ 10次，我们可以看到，最终 $x$ 接近最优解。

def gd(eta, f_grad):
    x = 10.0
    results = [x]
    for i in range(10):
        x -= eta * f_grad(x)
        results.append(float(x))
    print(f'epoch 10, x: {x:f}')
    return results

results = gd(0.2, f_grad)

epoch 10, x: 0.060466

优化 $x$ 的进展可以绘制如下：

def show_trace(results, f):
    n = max(abs(min(results)), abs(max(results)))
    f_line = torch.arange(-n, n, 0.01)
    d2l.set_figsize()
    d2l.plot([f_line, results],
             [[f(x) for x in f_line], [f(x) for x in results]], 'x', 'f(x)',
             fmts=['-', '-o'])

show_trace(results, f)

Learning Rate

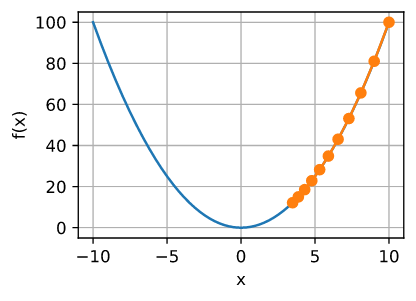
学习率 $\eta$ 可以由程序设计设设置。如果学习率太小，将会导致 $x$ 更新地太慢，需要更多地迭代次数得到更好的解。为了展示在这种情况下会发生什么，将相同优化问题的学习率 $\eta = 0.05$。正如我们所看到的，即使经过10个步骤，我们仍然离最优解很远。

show_trace(gd(0.05, f_grad), f)

epoch 10, x: 3.486784

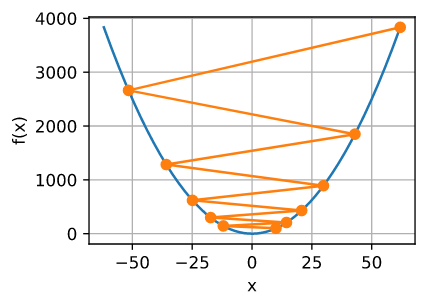
相反，如果我们使用过大的学习率， $\mid \eta f’(x) \mid$ 可能对于一阶泰勒展开公式过大。 $O(\eta^2) f’^2(x)$ 影响可能会非常大。在这种情况下，我们不能保证 $x$ 的迭代将会使得 $f(x)$ 的值变得更小。例如，当我们把学习率设置为 $\eta = 1.1$， $x$ 冲过了最优解 $x = 0$ 并且固件发散。

show_trace(gd(1.1, f_grad), f)

epoch 10, x: 61.917364

Local Minima

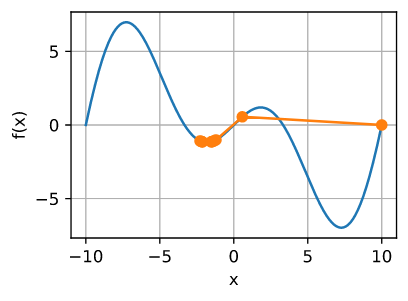
为了解释在非凸函数上会发生什么，我们假设 $f(x) = x · cos(cx)$, $c$为常数。这个函数有无穷多个局部极小值。根据我们对学习率的选择以及问题条件设置的好坏程度，我们最终可能会得到许多解决方案中的一个。下面的例子说明了高学习率如何导致较差的局部最小值。

c = torch.tensor(0.15 * np.pi)

def f(x):  # Objective function
    return x * torch.cos(c * x)

def f_grad(x):  # Gradient of the objective function
    return torch.cos(c * x) - c * x * torch.sin(c * x)

show_trace(gd(2, f_grad), f)

epoch 10, x: -1.528166

Multivariate Gradient Descent

现在我们对单变量情况有了更好的直觉，让我们考虑这样的情况，$x = [x_1, x_2, …, x_d]^T$。也就是说，目标函数 $f: \mathbb{R}^d \rightarrow \mathbb{R}$ 将向量映射为标量。因此，它的梯度也是多元的，它是一个由 $d$ 个偏导数组成的向量。

\[\nabla f(x) = [\frac{\partial f(x)}{\partial x_1}, \frac{\partial f(x)}{\partial x_2}, ..., \frac{\partial f(x)}{\partial x_d}]^T\]

梯度中的每个偏导元素 $\partial f(x) / \partial x_i$ 表示分别对每个输入 $x_i$ $f$ 在 $x$ 处的变化率。和之前一样，在单变量情况下，我们可以对多元函数使用相应的泰勒近似来得到我们的一些想法。

\[f(x + \epsilon) = f(x) + \epsilon^T \nabla f(x) + O(\| \epsilon\|^2)\]

换句话说，在 $\epsilon$ 的二阶项（$O(|\epsilon|^2)$）之前，最陡下降的方向是由负梯度 $-\nabla f(x)$ 给出的. 选择合适的学习率 $\eta > 0$ 产生原始的梯度下降算法。

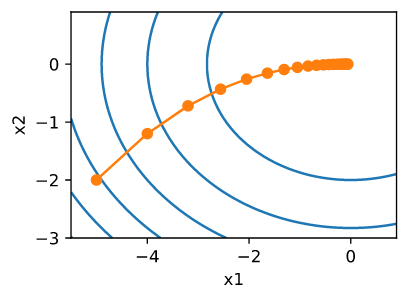
\[x \leftarrow x - \eta \nabla f(x)\]

为了了解算法在实践中的表现，让我们构造一个目标函数 $f(x) = x_1^2 + 2x_2^2$，输入是一个两维的向量 $x = [x_1, x_2]^T$，输出是一个标量。梯度由 $\nabla f(x) = [2x_1, 4x_2]^T$ 给定。我们将会观察到从初始位置 $[-5, -2]$ 通过梯度下降 $x$ 的轨迹。

首先，我们还需要两个辅助函数。第一种方法使用一个更新函数，并将其应用于初始值20次。第二个帮助可视化 $x$ 的轨迹。

def train_2d(trainer, steps=20, f_grad=None):  #@save
    """Optimize a 2D objective function with a customized trainer."""
    # `s1` and `s2` are internal state variables that will be used later
    x1, x2, s1, s2 = -5, -2, 0, 0
    results = [(x1, x2)]
    for i in range(steps):
        if f_grad:
            x1, x2, s1, s2 = trainer(x1, x2, s1, s2, f_grad)
        else:
            x1, x2, s1, s2 = trainer(x1, x2, s1, s2)
        results.append((x1, x2))
    print(f'epoch {i + 1}, x1: {float(x1):f}, x2: {float(x2):f}')
    return results

def show_trace_2d(f, results):  #@save
    """Show the trace of 2D variables during optimization."""
    d2l.set_figsize()
    d2l.plt.plot(*zip(*results), '-o', color='#ff7f0e')
    x1, x2 = torch.meshgrid(torch.arange(-5.5, 1.0, 0.1),
                            torch.arange(-3.0, 1.0, 0.1))
    d2l.plt.contour(x1, x2, f(x1, x2), colors='#1f77b4')
    d2l.plt.xlabel('x1')
    d2l.plt.ylabel('x2')

接下来，我们观察对于学习率 $\eta = 0.1$ ，优化变量 $x$ 的轨迹。我们可以看到在20步后， $x$ 的值在 $[0, 0]$ 接近它的最小值。尽管进展相当缓慢，但进展相当顺利。

def f_2d(x1, x2):  # Objective function
    return x1**2 + 2 * x2**2

def f_2d_grad(x1, x2):  # Gradient of the objective function
    return (2 * x1, 4 * x2)

def gd_2d(x1, x2, s1, s2, f_grad):
    g1, g2 = f_grad(x1, x2)
    return (x1 - eta * g1, x2 - eta * g2, 0, 0)

eta = 0.1
show_trace_2d(f_2d, train_2d(gd_2d, f_grad=f_2d_grad))

epoch 20, x1: -0.057646, x2: -0.000073

Adaptive Methods

正如我们在第11.3.1.1节中所看到的，要得到正确的学习速率 $\eta$ 是很困难的。如果我们选择的太小，我们取得的进步就很小。如果取的太大，解就会振荡，最坏的情况下它甚至会发散。如果我们可以自动地确定 $η$，或者完全不需要选择一个学习速率，那会怎么样呢？在这种情况下，不仅考虑目标函数的值和梯度，而且考虑其曲率的二阶方法会有所帮助。虽然由于计算成本，这些方法不能直接应用于深度学习，但它们提供了有用的直觉，帮助我们设计先进的优化算法，模拟以下列出的算法的许多理想特性。

Newton’s Method

回顾泰勒展开 $f： \mathbb{R}^d \rightarrow \mathbb{R}$ ，不需要在第一项后就停止。事实上，我们可以写成：

\[f(x + \epsilon) = f(x) + \epsilon^T \nabla f(x) + \frac{1}{2} \epsilon^T \nabla^2 f(x) \epsilon + O(\|\epsilon\|^3)\]

为了避免冗长的符号，我用定义 $H \mathop{=}^{def} \nabla^2 f(x)$ 表示 $f$ 的海森矩阵，它是一个 $d \times d$ 的矩阵。对于小的 $d$ 以及简单问题的 $H$ 是容易计算的。对于深度神经网络， $H$ 可能非常大，因为它的空间复杂度为 $O(d^2)$。此外，通过反向传播进行计算可能过于成本高。现在让我们忽略这些考虑，看看我们会得到什么算法。

最后，最小化 $f$ 满足 $\nabla f = 0$。下面的计算规则在 2.4.3 节中，通过忽略高阶项并且对 $\epsilon$ 求 11.3.8 的偏导，我们得到：

\[\nabla f(x) + H \epsilon = 0 \text{ and hence } \epsilon = -H^{-1} \nabla f(x)\]

也就是说，我们需要将海森矩阵 $H$ 转换为优化问题的一部分。

举一个简单的例子， $f(x) = \frac{1}{2} x^2$ , 我们有 $\nabla f(x) = x$ 并且 $H = 1$。因此对于任意的 $x$，我们得到 $\epsilon = -x$。只需一步就足以完美地收敛，无需任何调整。我们是幸运的：泰勒展开是准确的，因为 $f(x + \epsilon) = \frac{1}{2} x^2 + \epsilon x + \frac{1}{2} \epsilon$。

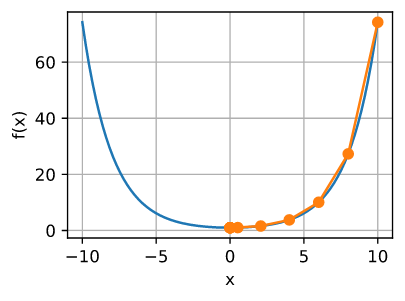
让我们看看在其他问题中会发生什么。对于一些常数 $c$，给定一个凸双曲余弦函数 $f(x) = cosh(cx)$，我们可以看到在一些迭代后达到全局最小值$x = 0$ 。

c = torch.tensor(0.5)

def f(x):  # Objective function
    return torch.cosh(c * x)

def f_grad(x):  # Gradient of the objective function
    return c * torch.sinh(c * x)

def f_hess(x):  # Hessian of the objective function
    return c**2 * torch.cosh(c * x)

def newton(eta=1):
    x = 10.0
    results = [x]
    for i in range(10):
        x -= eta * f_grad(x) / f_hess(x)
        results.append(float(x))
    print('epoch 10, x:', x)
    return results

show_trace(newton(), f)

epoch 10, x: tensor(0.)

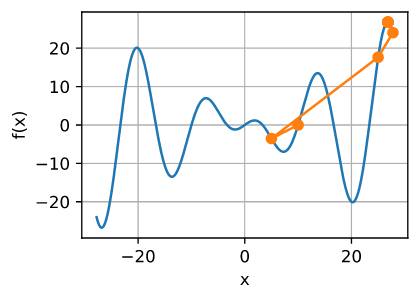
现在让我们考虑非凸函数 $f(x) = x cos(cx)$ , $c$ 为常数。请注意，在牛顿的方法中，我们最终除以了Hessian。这意味着，如果二阶导数是负的，我们可以走向 $f$ 的值增大的方向。这是算法的致命缺陷。让我们看看在实践中会发生什么。

c = torch.tensor(0.15 * np.pi)

def f(x):  # Objective function
    return x * torch.cos(c * x)

def f_grad(x):  # Gradient of the objective function
    return torch.cos(c * x) - c * x * torch.sin(c * x)

def f_hess(x):  # Hessian of the objective function
    return -2 * c * torch.sin(c * x) - x * c**2 * torch.cos(c * x)

show_trace(newton(), f)

epoch 10, x: tensor(26.8341)

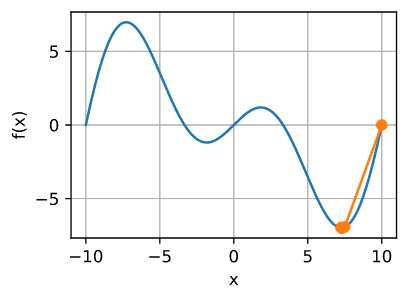
这很明显出错了。我们如何解决这个问题?一种方法是用它的绝对值来修正Hessian。另一个策略是回退学习率。这似乎没有达到目的，但也不是完全没有。有了二阶信息，我们可以在曲率较大时谨慎行事，在目标函数较平坦时采取较大的步长。让我们看看在稍微小一点的学习率下是如何工作的，比如 $\eta = 0.5$。如我们所见，我们有一个相当有效的算法。

show_trace(newton(0.5), f)

epoch 10, x: tensor(7.2699)

Convergence Analysis

对于凸三次可微的目标函数 $f$，我们只分析了牛顿法的收敛速度，其中二阶导数非零，例如 $f’’ > 0$。

多元证明是下面一维论证的直接延伸，省略了，因为它在直觉方面帮不了我们太多。

$x^{(k)}$ 表示第 $k$ 次迭代的 $x$ 的值并且 $e^{(k)} \mathop{=}^{def} x^{(k)} - x^*$ 表示在 $k^{th}$ 迭代距离最优解的距离。

通过泰勒展开式我们得到了这个条件 $f’(x^*) = 0$ 可以写作：

$0 = f'(x^{(k)} - e^{(k)}) = f'(x^{(k)}) - e^{(k)} f''(x^{(k)}) + \frac{1}{2} (e^{(k)})^2 f'''(\xi^{(k)})$ 其中 $\xi^{(k)} \in [x^{(k)} - e^{(k)}, x^{(k)}]$，上面展开式除以 $f’‘(x^{(k)})$ 得到：

\[e^{(k)} - \frac{f'(x^{(k)})}{f''(x^{(k)})} = \frac{1}{2}(e^{k})^2 \frac{f'''(\xi^{(k)})}{f''(x^{(k)})}\]

回想一下，我们有这个更新 $x^{(k+1)} = x^{(k)} / f’‘(x^{(k)})$。代入这个更新方程然后两边取绝对值，我们得到

\[\mid e^{(k + 1)} \mid = \frac{1}{2} (e^{(k)})^2 \frac{f'''(\xi^{(k)})}{f''(x^{(k)})}\]

因此，当我们在一个有界的区域 $\mid f’’’(\xi^{(k)}) \mid / (2 f’‘(x^{(k)})) \leq c$，我们有一个二次递减的误差

\[\mid e^{(k+1)} \leq c(e^{(k)})^2\]

顺便提一下，优化研究人员称之为线性收敛，而像这样的条件 $\mid e^{(k + 1)} \mid \leq \alpha \mid e^{(k)} \mid$ 会被叫做收敛率常数。请注意，此分析带有一些注意事项。首先，我们并不能真正保证我们将在何时到达快速收敛的区域。其次，这种分析要求 $f$ 在高阶导数下表现良好。它可以归结为根据它的值可能的变化，确保 $f$ 不会有产生意料之外结果。

Preconditioning

毫不奇怪，计算和存储整个Hessian是非常昂贵的。

因此，寻找替代方案是可取的。改善问题的一个方法是 preconditioning。它避免计算整个Hessian，但只计算对角线项。

\[x \leftarrow x - \eta diag(H)^{-1} \nabla f(x)\]

虽然不如完整的牛顿方法，但总比不使用要好。为了了解为什么这可能是一个好想法，考虑这样一种情况: 一个变量代表高度，单位是毫米，另一个也代表高度，单位是公里。假设这两个自然尺度都是以米为单位的，我们在参数化上有一个糟糕的不匹配。幸运的是，使用 preconditioning 可以消除这个问题。有效的梯度下降预处理相当于为每个变量(向量 $x$ 的坐标)选择不同的学习率。正如我们稍后将看到的，preconditioning 推动了随机梯度下降优化算法的一些创新。

Gradient Descent with Line Search

梯度下降的一个关键问题是我们可能会超过目标或进展不足。解决这个问题的一个简单方法是将 Line Search 与梯度下降结合使用。我们使用由 $\nabla f(x)$ 给定的方向，然后使用二分查找什么样的学习率 $\eta$ 最小化 $f(x - \eta \nabla f(x))$。

这个算法收敛非常快。然而，对于深度学习的目的来说，这并不太可行，因为 Line Search 的每一步都需要我们在整个数据集上评估目标函数。这花销太大了。

【d2l】Gradient Descent