Basics

Leaky Averages

上一节讨论了将minibatch SGD作为加速计算的一种方法。它有一个好处是通过平均梯度减小了方差的大小。 小批量随机梯度下降可以由以下公式计算：

为了使符号表示简单， 我们使用 $h_{i, t-1} = \partial_w f(x_i, w_{t-1})$ 表示对于样本 $i$ 在时间 $t-1$ 使权重更新的随机梯度下降。如果我们可以从方差减小这件事情上受益， 甚至可以不仅在一个 minibatch 上平均梯度， 那就太好了。 完成这一任务的一种方法是用 “leaky average” 替换梯度计算。

对于某些 $\beta \in (0, 1)$。 这有效地将当前梯度替换为在多个过去梯度上平均的梯度。$v$ 叫做动量。 将 $v$ 展开得到：

大的 $beta$ 导致更长程的平均， 而小的 $\beta$ 只做了小的纠正。新的梯度替换不再指向某一特定情况下最陡下降的方向，而是指向过去梯度的加权平均方向。这使得我们在不计算整个样本集梯度的情况下， 得到了整个样本集平均梯度的收益。

上面的推理形成了现在的加速梯度方法的基础 ，例如带动量的梯度。在优化问题是病态的情况下，它们还能更有效地解决问题。

An Ill-conditioned Problem

为了更好地理解动量法的几何性质，我们重新讨论梯度下降法，尽管目标函数不太好。我们使用 $f(x) = x_1^2 + 2x_2^2$， 一个有些变形的椭球目标。 我们进一步使这个函数变形：

像之前一样， $f$ 它的最小值在 $(0, 0)$。 这个函数在 $x_1$ 的方向上非常平。 让我们看看当我们像之前一样对这个新函数进行梯度下降时会发生什么。我们使用学习率 0.4。

1
2
3
4
5
6
7
8
9
10
11
%matplotlib inline
import torch
from d2l import torch as d2l

eta = 0.4
def f_2d(x1, x2):
    return 0.1 * x1 ** 2 + 2 * x2 ** 2
def gd_2d(x1, x2, s1, s2):
    return (x1 - eta * 0.2 * x1, x2 - eta * 4 * x2, 0, 0)

d2l.show_trace_2d(f_2d, d2l.train_2d(gd_2d))

1
epoch 20, x1: -0.943467, x2: -0.000073

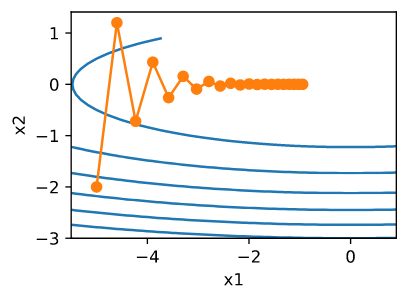
经过这样构造之后， $x_2$ 方向的梯度远比 $x_1$ 方向变化地更快。 如果我们选择小的学习率我们可以确保在 $x_2$ 方向上不会发散， 但是我们在 $x_1$ 方向上却难以收敛。 如果我们选择大学习率 $x_1$ 会快速地取得进展， 但是在 $x_2$ 上会发散。 下面的例子解释了从 0.4 到 0.6 缓慢增加学习率会发生什么。 $x_1$ 方向收敛，但是整体解的质量非常糟糕。

1
2
eta = 0.6
d2l.show_trace_2d(f_2d, d2l.train_2d(gd_2d))

1
epoch 20, x1: -0.387814, x2: -1673.365109

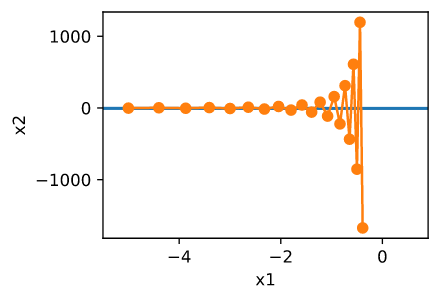
The Momentum Method

动量法允许我们解决上面描述的梯度下降问题。看看上面的优化轨迹，我们可能会直觉地认为平均过去的梯度效果会很好。在 $x_1$ 方向上累计梯度， 会增加每一步的距离。 在 $x_2$ 方向上梯度震荡， 累积的梯度将会由于震荡减少步长。 使用 $v_t$ 而不是使用梯度 $g_t$, 将会产生以下更新公式：

当 $\beta = 0$ 时， 恢复为普通的梯度下降。 在深入研究数学属性之前，让我们快速了解一下算法在实践中的表现。

1
2
3
4
5
6
7
def momentum_2d(x1, x2, v1, v2):
    v1 = beta * v1 + 0.2 * x1
    v2 = beta * v2 + 4 * x2
    return x1 - eta * v1, x2 - eta * v2, v1, v2

eta, beta = 0.6, 0.5
d2l.show_trace_2d(f_2d, d2l.train_2d(momentum_2d))

1
epoch 20, x1: 0.007188, x2: 0.002553

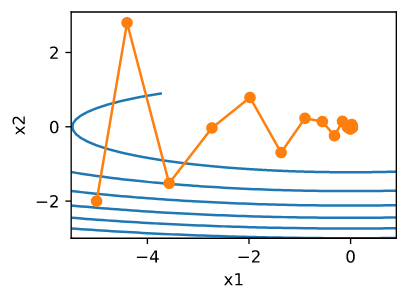
正如我们所看到的，即使使用我们之前使用的相同的学习速率，动量仍然可以很好地收敛。让我们看看当我们减小动量参数时会发生什么。将它减小为一半 $\beta = 0.25$ 导致了一个很难收敛的轨迹。但无论如何， 这都要比没有动量要好。

1
2
eta, beta = 0.6, 0.25
d2l.show_trace_2d(f_2d, d2l.train_2d(momentum_2d))

1
epoch 20, x1: -0.126340, x2: -0.186632

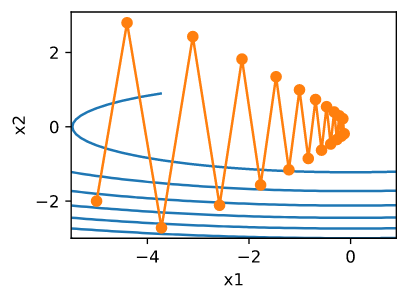
注意，我们可以将动量和随机梯度下降结合起来，特别是，小批量随机梯度下降。唯一要做的变化就是用 $g_t$ 替换掉梯度 $g_{t, t-1}$。 最后， 为了方便我们在时间 $t = 0$ 初始化 $v_0 = 0$。 让我们来看一下 leaky averaging 对更新实际做了什么。

Effective Sample Weight

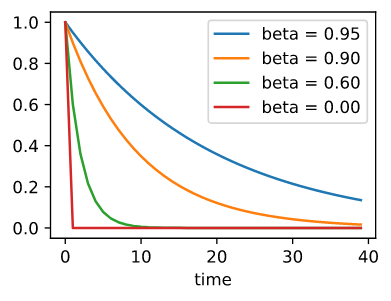
回忆一下 $v_t = \sum_{\tau=0}^{t-1} \beta^\tau g_{t - \tau, t - \tau - 1}$。 取极限，这些项加起来是 $\sum_{\tau=0}^\infty \beta^\tau = \frac{1}{1-\beta}$。 换句话说， 与其在梯度下降或者随机梯度下降中采用步长大小为 $\eta$， 我们使用步长大小为 $\frac{\eta}{1 - \beta}$， 这样做可能将会有更好表现的梯度方向。 为了解释不同 $\beta$ 的选择对权重表现的影响，绘制如下的表格 ：

1
2
3
4
5
6
7
d2l.set_figsize()
betas = [0.95, 0.9, 0.6, 0]
for beta in betas:
    x = torch.arange(40).detach().numpy()
    d2l.plt.plot(x, beta**x, label=f'beta = {beta:.2f}')
d2l.plt.xlabel('time')
d2l.plt.legend();

Theoretical Analysis

$f(x) = 0.1 x_1^2 + 2x_2^2$ 看起像是人为创造的。 我们现在会看到，这实际上是一个很有代表性的问题，至少在最小化凸二次目标函数的情况下。

Quadratic Convex Functions

考虑下面的函数

这是一个通用的二次函数。对于正定矩阵 $Q \succ 0$，例如， 对于有正特征值的矩阵在 $x^* = -Q^{-1}c$ 是极小值点 并且 极小值为 $b - \frac{1}{2} c^T Q^{-1} c$。 因此我们可以重写 $h$ 为：

梯度为 $\partial_x f(x) = Q(x - Q^{-1}c)$。 也就是说， 它取决于 $x$ 之间的局咯 以及 极小值点和 $Q$ 的乘积。 因此动量是 $Q(x_t - Q^{-1}c)$ 的线性组合。

因为 $Q$是正定的， 它可以通过 $Q = O^T \Lambda O$分解为特征值和特征向量， $O$为正交矩阵， $\Lambda$ 为正特征值的对角矩阵。 这里我们可以实现一个代换： $z := O(x - Q^{-1}c)$ 以得到简化表达式：

这里 $b’ = b - \frac{1}{2}c^TQ^{-1}c$。 因为 $O$ 是正交矩阵， 它不会影响梯度。 表达式中 $z$ 的梯度下降变为：

这个表达式中重要的事实是梯度下降不会在不同的特征空间中混合。优化问题以协调的方式进行：

在此过程中，我们证明了以下定理:凸二次函数的有动量和无动量梯度下降分解为二次矩阵特征向量方向上的坐标优化。

Scalar Functions

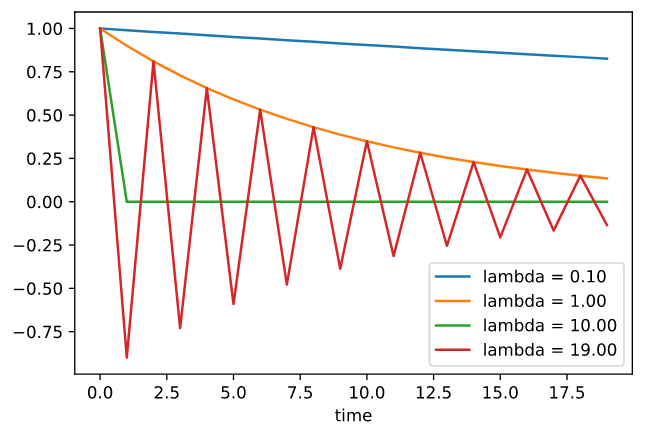
根据上面的结果，让我们看看当我们最小化这个函数 $f(x) = \frac{\lambda}{2}x^2$ 时会发生什么。 对于梯度下降我们有：

当 $\mid 1 - \eta \lambda \mid < 1$， 这个优化以指数速率收敛， 因为在 $t$ 步之后， 我们有 $x_t = (1 - \eta \lambda)^t x_0$。 这表明了收敛速率如何提升， 当我们增加学习率 $\eta$ 直到 $\eta \lambda = 1$。

1
2
3
4
5
6
7
8
lambdas = [0.1, 1, 10, 19]
eta = 0.1
d2l.set_figsize((6, 4))
for lam in lambdas:
    t = torch.arange(20).detach().numpy()
    d2l.plt.plot(t, (1 - eta * lam)**t, label=f'lambda = {lam:.2f}')
d2l.plt.xlabel('time')
d2l.plt.legend();

为了分析动量情况下的收敛性，我们首先用两个标量来重写更新方程： 一个是 $x$， 另一个是动量 $v$。 这将产生：

我们使用 $2 \times 2$ 的 $R$ 控制收敛表现。 在初始选择 $[v_0, x_0]$ $t$步之后变成 $R(\beta, \eta, \lambda)^t [v_0, x_0]$。 因此， 收敛速度取决于 $R$ 的特征值。 $0 < \eta \lambda < 2 + 2\beta$ 动量收敛。 这比梯度下降的 $0 < \eta \lambda < 2$ 有更大的可行参数范围。 这也表明通常更大 $\beta$ 更好。

• Previous
  【d2l】Stochastic Gradient Descent
• Next
  【d2l】Adagrad