11.7 节中的一个关键问题是预定义的学习率衰减效率是 $O(t^{-\frac{1}{2}})$。 虽然这通常适用于凸问题,但对于非凸问题(如在深度学习中遇到的问题)可能不太理想。 Adagrad的坐标级自适应作为预条件是很好的。
Tieleman & Hinton, 2012 等人 提出了RMSProp算法将速率调度与坐标自适应学习速率解耦。这个问题是 Adagrad 累计梯度的平方 $g_t$ 到一个状态向量 $s_t = s_{t-1} + g_t^2$。 因为缺少规范化, $s_t$ 没有界地持续上涨。
一种修复这个问题的方法是使用 $s_t / t$。 对于合理的 $g_t$ 的分布, 这将会收敛。不幸的是直到限制行为开始起作用可能会花费很长时间, 因为程序记住了值的全部轨迹。 另一种方法是使用 Leaky Average, 比如对于某些参数 $\gamma > 0$, $s_t \leftarrow \gamma s_{t-1} + (1 - \gamma)g_t^2$。 保持其他部分不变产生 RMSProp。
The Algorithm
让我们把这些等式详细地写出来。
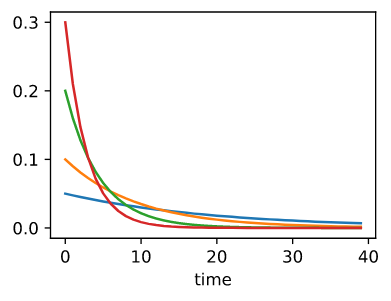
\[s_t \leftarrow \gamma s_{t-1} + (1 - \gamma) g_t^2\] \[x_t \leftarrow x_{t-1} - \frac{\eta}{\sqrt{s_t + \epsilon}} \odot g_t\]和 11.6 节一样, 我们使用 $1 + \gamma + \gamma^2 + … = \frac{1}{1-\gamma}$。 让我们来可视化一下不同 $\gamma$ 的选择在过去 40 个时间步的权重。
1
2
3
4
5
6
7
8
9
10
import math
import torch
from d2l import torch as d2l
d2l.set_figsize()
gammas = [0.95, 0.9, 0.8, 0.7]
for gamma in gammas:
x = torch.arange(40).detach().numpy()
d2l.plt.plot(x, (1 - gamma) * gamma**x, label=f'gamma = {gamma:.2f}')
d2l.plt.xlabel('time');