Abstract

将transformer从语言迁移到视觉， 存在一些差异， 比如视觉上尺度与像素的高分辨率。 我们提出一种层级Transformer通过 shift windows 计算表征。 shift widnows方法在允许跨窗口连接的情况下， 通过限制self-attention对非重叠局部窗口的计算提高了效率。 层级结构使得模型在不同尺度上有灵活性， 并且随着图像尺寸大小增大线性增加计算复杂度。

Introduction

将语言域的高表现迁移到视觉域上的挑战可以解释为两种模态间的差异。一个差异是尺度。另外一个差异是图像有相比于文本多得多的像素。

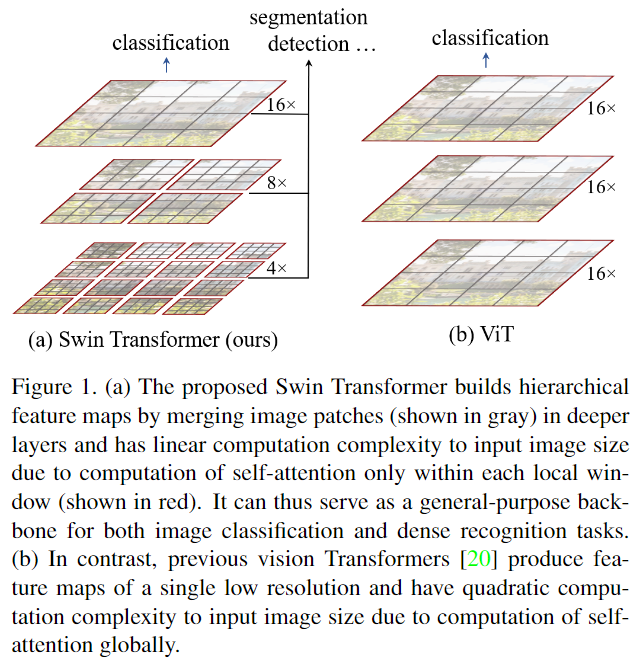
如上图所示， 通过先从小的patch开始， 在深层的Transformer逐渐融合周围的patch构造层级的表征。线性计算复杂度通过在非重叠的窗口间计算Self-Attention实现。

Swin Transformer的一个关键设计是在连续的 self-attention 层之间窗口滑动。这种策略使得一个窗口中的所有 query patches 共享相同的 key set，在硬件上加速了内存的读取。

Method

Overall Architecture

Swin Transformer 的结构如下图所示。它首先通过 patch split 模块将 RGB 图像拆分为非重叠的 patches， 像ViT一样。每个 patch 被看做一个 “token”， 并且它的特征被设为原始RGB像素值的拼接。这里使用 patch 大小为 $4 \times 4$， 因此每个 patch 的特征维度为 $4 \times 4 \times 3 = 48$。上使用一个线性 embedding 层将 raw-value 特征投影为任意的维度(表示为 $C$)。

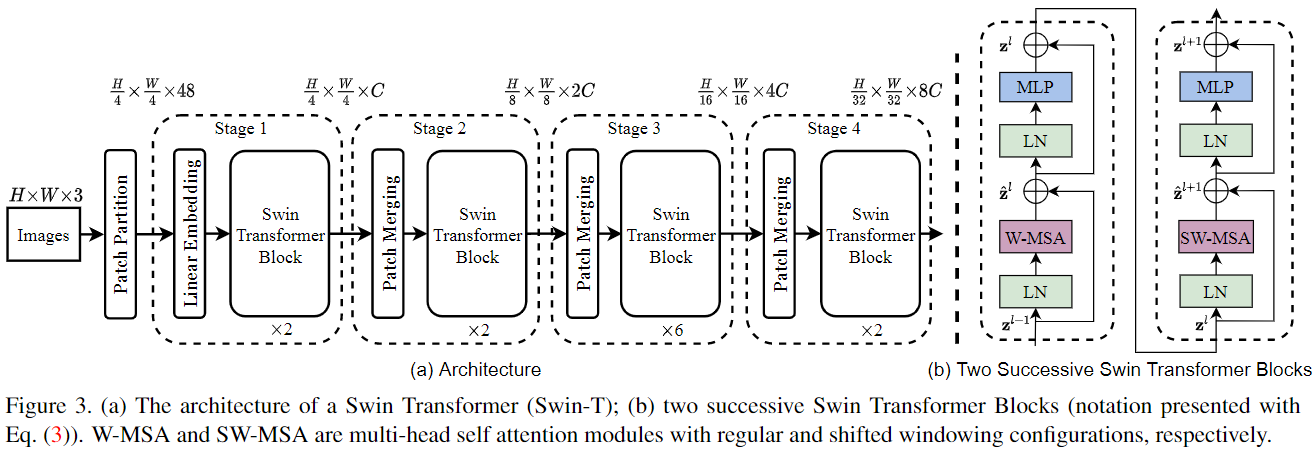
几个带有 Swin Transformer blocks 的自注意力计算用于这些 patch tokens。 Transformer blocks 保持tokens的数量为 $(\frac{H}{4} \times \frac{W}{4})$， 加上一个线性 embedding 层叫做 Stage 1。

为了产生层次化的表征， tokens的数量会随着网络的加深通过 patch merging 减少。 第一个 patch merging 层拼接每个相邻 $2 \times 2$的 patches的特征， 然后对拼接的 $4C$ 维度使用一个线性层。 这将以 $2 \times 2 = 4$ 的速度减少 tokens 的数量， 输出维度被设置为 $2C$。Swin Transformer block 被用在特征变换之后， 分辨率保持在 $\frac{H}{8} \times \frac{H}{8}$。第一个patch merging 和 特征变换被表示为 Stage 2。 这个过程重复两次， 即 Stage 3 和 Stage 4， 输出的分辨率分别为 $\frac{H}{16} \times \frac{W}{16}$ 和 $\frac{H}{32} \times \frac{W}{32}$。 这些 stages 联合产生层次化的表征， 像典型的卷积神经网络一样。

Swin Transformer block Swin Transformer 将 multi-head self attention(MSA) 模块替换为一个基于shift widnows 的模块， 其他结构保持不变。 Swin Transformer block 由一个基于MSA的shift widnows， 接着一个两层的 MLP 和在它们之间的GELU 非线性激活组成。 LayerNorm(LN) 用于每个 MSA 和 MLP 之间， 并且在每个模块之后加入残差连接。

Shifted Window based Self-Attention

Self-attention in non-overlapped windows 为了有效建模，提出在局部窗口内计算self-attention。窗口以非重叠的方式均匀地划分图像。假设每个窗口包含 $M \times M$ 个 patches， 全局 MSA 模块和一个基于窗口的MSA在一个 $h \times w$ patches 图像上的计算复杂度为：

前者是 patch 数量 $hw$ 的二次方被， 后者当 $M$ 固定时是线性的(默认为7)。

Shifted window partitioning in successive blocks 基于窗口的 self-attention 缺乏跨窗口之间的连接， 这限制了它的建模能力。为了维持非重叠窗口的计算有效性的同时引入跨窗口连接， 提出了 shifted window partitioning 方法， 在Swin Transformer blocks 中交替使用两种 partition。

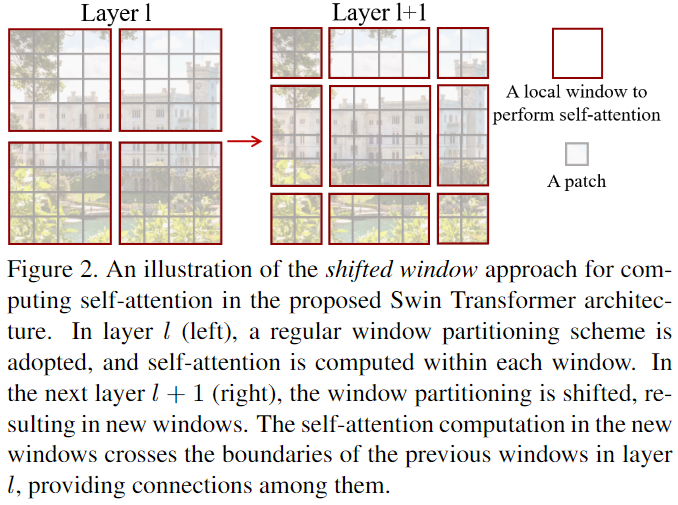
如上图所示， 第一个模块使用均匀规则的窗口划分策略， 他从左上角像素开始， $8 \times 8 $ 的特征图被划分为 $2 \times 2$ 个大小为 $4 \times 4$ (M=4)的窗口。

有了 shifted window partitioning 方法， 连续的 Swin Transformer blocks 被计算为：

其中 $\hat z^l$ 和 $z^l$ 分别表示 块 $l$ 的 (S)W-MSA模块 和 MLP 模块的特征。W-MSA 和 SW-MSA 表示使用均匀划分策略 和使用 shifted window 配置划分策略的 window based multi-head self-attention。

shifted window 划分策略在之前层的相邻不重叠窗口之间引入了连接， 这在计算机视觉任务上十分有效。

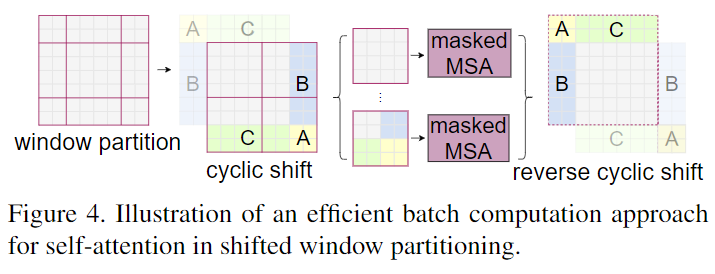
Efficient batch computation for shifted configuration： shifted window partitioning 的一个问题是他会导致更多的窗口， 从 $\lceil \frac{h}{M}\rceil \times \lceil \frac{w}{M} \rceil$ 到 $(\lceil \frac{h}{M} \rceil + 1) \times (\lceil \frac{w}{M} \rceil + 1)$， 一些窗口回避 $M \times M$ 更小。 一个简单的方法是padding 这些更小的窗口到 $M \times M$ 大小， 并且在计算 attention 时 mask 掉这些 padding 的位置。当以 regular partitioning 方式时， 窗口数量很小， 例如 $2 \times 2$， 这种简单的方法增加的计算复杂度是很多的 ($2 \times 2 \rightarrow 3 \times 3$)。这里提出了一种 batch computation 方法， 它向左上角 cyclic-shifting， 如下图所示。在 shift 之后， 一个 batched window 可能由几个在特征图中不相邻的子窗口组成， 因此使用 mask 机制用于限制每个子窗口的 self-attention 计算。

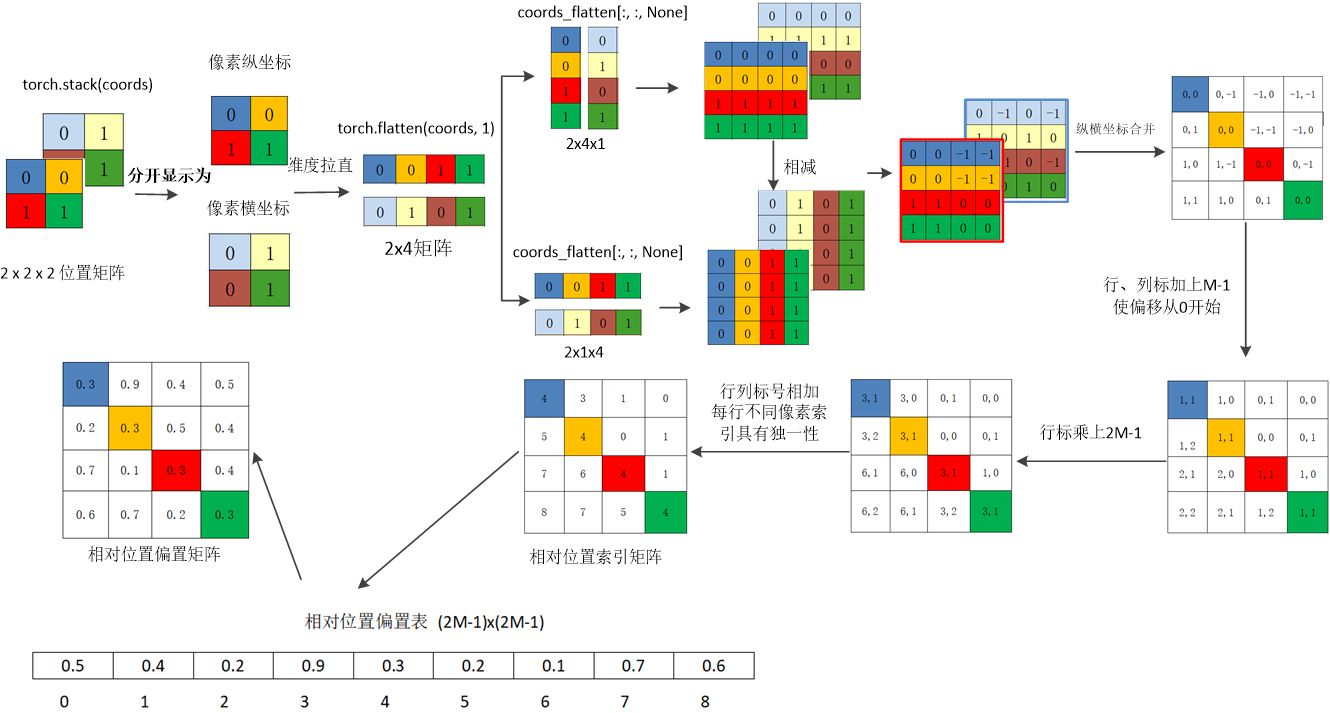
Relative position bias 为了计算 self-attention， 将相对位置偏差 $B \in \mathbb{R}^{M^2 \times M^2}$ 引入到每个计算头计算相似度中：

其中 $Q, K, V \in \mathbb{R}^{M^2 \times d} $, $M^2$ 是每个窗口中 patch 的数量。 因为相对位置每个州的取值范围为 $[-M+1, M - 1]$， 我们参数化 bias 矩阵为 $\hat B \in \mathbb{R}^{(2M-1) \times (2M -1)}$。

Conclusion

这篇文章提出一种叫做 Swin Transformer的新的 Vision Transformer 的结构， 它会产生层级的特征表示， 并且对于输入图像的尺寸具有线性增长的计算复杂度。

Swin Transformer 的一个关键设计， 基于 shifted window 的 self-attention 在视觉人物上表现出有效性。

Reference

1. Swin Transformer之相对位置编码详解

• Previous
  【深度学习】Revisiting ResNets: Improved Training and Scaling Strategies
• Next
  【深度学习】Uformer：A General U-Shaped Transformer for Image Restoration